-

人教部编版语文九年级下册任务三演出与评议教案
从以下话题中任选其一(也可自选话题),写一篇作文,谈谈自己对剧本和戏剧表演的认识。不少于600字。①我为什么对“他”印象最深②舞台说明不只是“说明”③戏剧冲突面面观④台词应该怎样说⑤肢体语言很重要⑥配角也要演到位⑦“好戏”是配合出来的2.技法点拨。①写作时,结合对剧本和戏剧表演的认识,发表自己的见解和看法,力求明白晓畅,切勿写得深奥晦涩难懂。②阐述认识时,要列举剧本和戏剧表演的实例进行分析,便于读者理解和信服。③涉及把握不准的专业术语需查阅相关资料、典籍,规避错误,以免误导读者。④明确提出观点,筛选典型事例作为依据,分析材料与观点之间的关系。师:无论是选择哪一个话题,都要结合具体的实例进行分析,不能只列条目而无内容。针对某一戏剧或谈人物,或谈舞台说明,或谈矛盾冲突,或谈肢体语言,或谈相互配合等;也可以针对某个话题,列举多部戏剧中具体的一句、一段话,或一幕。

人教部编版语文九年级下册任务一阅读与思考教案
结束语:通过这节课的探究,我们了解了本单元三部戏剧的背景和主旨,相信大家对剧本的理解更深了。下节课,我们就要准备排练戏剧,希望大家课下再好好读读剧本,加深理解。五、布置作业1.课后查阅关于表演的相关资料,了解表演的知识。2.选择最喜欢的一个剧本熟读,并选择其中最喜欢的一个人物,揣摩应如何表演。剧本学习是一项新的教学内容,本次教学设计主要以人物为核心,从三个方面展开:(1)从文本的角度读剧本。从基本的情节入手,通过理解情节中的矛盾冲突来感知人物形象,让学生建立对剧本的基本理解。(2)从表演的角度读剧本。训练学生的朗读能力,引导学生通过台词来理解人物,为下阶段的舞台表演打下基础。(3)从现实的角度读剧本。指导学生认识剧本的现实意义,促进学生的成长。

人教部编版语文九年级下册写作有创意的表达教案
1.题目具有开放性,可以实写,也可以虚写。展开联想和想象,将自己想到的全列出来,然后再从中确定写作重点。2.从题目看,可以灵活选择文体。比如,可以以写景或抒情为主,也可以进行议论,或者虚构一个故事等,要力求有创意。3.注意表达上的创新,丰富的词语、恰当的修辞等,都可以为文章增色。2.写作指导。(1)审题立意。本题具有开放性,有实虚两重意义。展开联想和想象,可以写实,也可以写它的象征意义,还可以实虚结合。“春天的色彩”既可以指现实中的春天的各种色彩,也可以指象征意义中的“春天”带着“色彩”(以表达某种心情)。如自然的春天、社会的春天、心灵的春天等等。(2)文体选择与表达。在文体方面,可以写成写景或抒情的散文,也可以写议论文,或者写成表达“春天的色彩”这一主题的记叙文。在表达上应有创新,可以用丰富的词汇、变换的句式、新颖的修辞为文章增色。尤其在作文形式上要有所创新。

人教部编版语文九年级下册祖国啊,我亲爱的祖国教案
诗歌创作个性十足,难以用统一的规律去分析,然而发掘一些欣赏诗歌的一般性的思路和角度,可以让阅读诗歌有章可循,减少学生读诗时的畏难情绪。在第1课时中,我以朗读为贯穿课堂的抓手,让学生通过思考“怎么读”,自觉地去发现并分析诗歌中的意象,理解诗歌大意,让学生对诗歌有初步的理解和体会。第2课时在整体把握诗歌的基础上,具体去分析诗歌中富有表现力的语言,训练学生深入思考的能力,引导学生梳理诗歌的情感脉络,体会诗中作者的情感变化,理解诗人想要表达的真挚情感,并通过拓展阅读让学生尝试自己解读诗歌,帮助学生巩固所学的阅读诗歌的方法。两节课的侧重点不同,但都围绕这首诗的特点和整体教学思路进行规划,做到“一课一得”。写作背景舒婷初中毕业后下乡插队,后又当过工人。在国家蒙难、人民遭殃的非常岁月,备尝艰辛的舒婷,内心的迷惘、痛苦可想而知。1978年12月,中国迎来了具有重大历史意义的十一届三中全会,开启了改革开放的历史新时期。1979年4月,诗人面对祖国摆脱苦难、正欲奋飞的情景,以自己独有的抒情方式写下了此诗。

北师大初中七年级数学上册比较线段的长短教案1
1.了解“两点之间,线段最短”.2.能借助尺、规等工具比较两条线段的大小,能用圆规作一条线段等于已知线段.3.了解线段的中点及线段的和、差、倍、分的意义,并能根据条件求出线段的长.一、情境导入爱护花草树木是我们每个人都应具备的优秀品质.从教学楼到图书馆,总有少数同学不走人行道而横穿草坪(如图),同学们,你觉得这样做对吗?为了解释这种现象,学习了下面的知识,你就会知道.二、合作探究探究点一:线段长度的计算【类型一】 根据线段的中点求线段的长如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.(1)求线段MN的长;(2)根据(1)中的计算过程和结果,设AB=a,其它条件不变,你能猜出MN的长度吗?请用简洁的话表达你发现的规律.

北师大初中七年级数学上册比较线段的长短教案2
教学反思: 1.本课时设计的主导思想是:将数形结合的思想渗透给学生,使学生对数与形有一个初步的认识.为将来的学习打下基础,这节课是一堂起始课,它为学生的思维开拓了一个新的天地.在传统的教学安排中,这节课的地位没有提到一定的高度,只是交给学生比较线段的方法,没有从数形结合的高度去认识.实际上这节课大有可讲,可以挖掘出较深的内容.在教知识的同时,交给学生一种很重要的数学思想.这一点不容忽视,在日常的教学中要时时注意.2.学生在小学时只会用圆规画圆,不会用圆规去度量线段的大小以及截取线段,通过这节课,学生对圆规的用法有一个新的认识.3.在课堂练习中安排了度量一些三角形的边的长度,目的是想通过度量使学生对“两点之间线段最短”这一结论有一个感性的认识,并为下面的教学做一个铺垫.

北师大初中七年级数学上册代数式的求值教案1
(1)请你用代数式表示水渠的横断面面积;(2)计算当a=3,b=1时,水渠的横断面面积.解析:(1)根据梯形面积=12(上底+下底)×高,即可用含有a、b的代数式表示水渠横断面面积;(2)把a=3、b=1带入到(1)中求出的代数式中,其结果即为水渠的横断面面积.解:(1)∵梯形面积=12(上底+下底)×高,∴水渠的横断面面积为:12(a+b)b(m2);(2)当a=3,b=1时水渠的横断面面积为12(3+1)×1=2(m2).方法总结:解答本题时需搞清下列几个问题:(1)题目中给出的是什么图形?(2)这种图形的面积公式是什么?(3)根据公式求图形的面积需要知道哪几个量?(4)这些量是否已知或能求出?搞清楚了这些问题,求解就水到渠成.三、板书设计教学过程中,应通过活动使学生感知代数式运算在判断和推理上的意义,增强学生学习数学的兴趣,培养学生积极的情感和态度,为进一步学习奠定坚实的基础.

北师大初中七年级数学上册代数式的求值教案2
解 由题意可得,今年的年产值为a·(1+10%) 亿元,于是明年的年产值为a·(1+10%)·(1+10%)= 1.21a(亿元).若去年的年产值为2亿元,则明年的年产值为1.21a =1.21×2 = 2.42(亿元).答:该企业明年的年产值将能达到1.21a亿元.由去年的年产值是2亿元,可以预计明年的年产值是2.42亿元.例3 当x=-3时,多项式mx3+nx-81的值是10,当x = 3时,求该代数式的值.解 当x=-3时,多项式mx3+nx-81=-27m-3n-81, 此时-27m-3n-81=10, 所以27m+3n=-91.则当x=3,mx3+nx-81 =( 27m+3n )-81=-91-81=-172.注:本题采用了一种重要的数学思想——“整体思想”.即是考虑问题时不是着眼于他的局部特征,而是把注意力和着眼点放在问题的整体结构上,把一些彼此独立,但实质上又相互紧密联系着的量作为整体来处理的思想方法.

北师大初中七年级数学上册多边形和圆的初步认识教案1
方法总结:在分辨一个图形是否为多边形时,一定要抓住多边形定义中的关键词语,如“线段”“首尾顺次连接”“封闭”“平面图形”等.如此,对于某些似是而非的图形,只要根据定义进行对照和分析,即可判定.探究点二:确定多边形的对角线一个多边形从一个顶点最多能引出2015条对角线,这个多边形的边数是()A.2015 B.2016 C.2017 D.2018解析:这个多边形的边数为2015+3=2018.故选D.方法总结:过n边形的一个顶点可以画出(n-3)条对角线.本题只要逆向求解即可.探究点三:求扇形圆心角将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,求这三个扇形圆心角的度数.解析:用扇形圆心角所对应的比去乘360°即可求出相应扇形圆心角的度数.解:三个扇形的圆心角度数分别为:360°×22+3+4=80°;360°×32+3+4=120°;

北师大初中七年级数学上册利用去分母解一元一次方程教案2
先让学生自己总结,然后互相交流,得出结论。解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式。解题时,要灵活运用这些步骤。板书:解一元一次方程一般步骤:1、 去分母-----等式性质22、 去括号----去括号法则3、 移项----等式性质14、 合并同类项----合并同类项法则5、 系数化为1.----等式性质2【课堂练习】练习:解下列一元一次方程解方程: (2) ;思路点拔:(1)去分母所选的乘数应是所有分母的最小公倍数,不应遗漏。(2)用分母的最小公倍数去乘方程的两边时,不要漏掉等号两边不含分母的项。(3)去掉分母后,分数线也同时去掉,分子上的多项式用括号括起来。回顾解以上方程的全过程,表示了一元一次方程解法的一般步骤,通过去分母—去括号—移项—合并同类项—系数化为1等步骤,就可以使一元一次方程逐步向着 =a的形式转化。

北师大初中七年级数学上册截一个几何体教案1
解析:当截面与轴截面平行时,得到的截面的形状为长方形;当截面与轴截面斜交时,得到的截面的形状是椭圆;当截面与轴截面垂直时,得到的截面的形状是圆,所以截面的形状不可能是三角形.故选A.方法总结:用平面去截圆柱时,常见的截面有圆、椭圆、长方形、类似于梯形、类似于拱形等.探究点三:截圆锥问题一竖直平面经过圆锥的顶点截圆锥,所得到的截面形状与下图中相同的是()解析:经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线.如图,由图可知得到的截面是一个等腰三角形.故选B.方法总结:用平面去截圆锥,截面的形状可能是三角形、圆、椭圆等.三、板书设计教学过程中,强调学生自主探索和合作交流,经历操作、抽象、归纳、积累等思维过程,从中获得数学知识与技能,发展空间观念和动手操作能力,同时升华学生的情感态度和价值观.
北师大初中七年级数学上册截一个几何体教案2
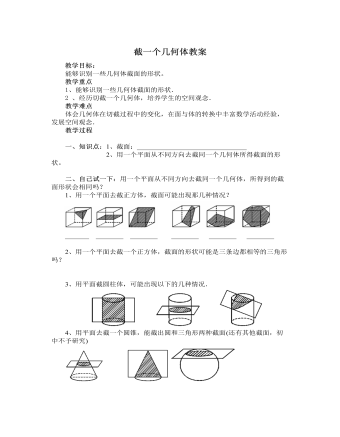
[例3]、用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是_________。四、巩固强化:1、一个正方体的截面不可能是( )A、三角形 B、梯形 C、五边形 D、七边形2、用一个平面去截五棱柱,边数最多的截面是_______形.3*、用一个平面去截几何体,若截面是三角形,这个几何体可能是__________________________________________________.4*、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如虹截面是三角形呢?5*、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?6*、几何体中的圆台、棱锥都是课外介绍的,所以我们就在这个栏目里继续为大家介绍这两种几何体的截面.(1)圆台用平面截圆台,截面形状会有_____和_______这两种较特殊图形,截法如下:

北师大初中七年级数学上册利用去括号解一元一次方程教案2
小明说:“我姐姐今年的年龄是我去年的年龄的2倍少6,”已知姐姐今年20岁,问小明今年几岁?若取小明今年为x岁,则依据下面的等量关系式列方程:姐姐今年的年龄=小明去年年龄的2倍-6.得2(x-1)-6=20.例5解方程-3(x+1)=9总结:根据乘法分配律和去括号法则(括号前面是“+”号,把“+”号和括号去掉,括号内各项都不改变符号;括号前面是“-”号,把“-”号和括号去掉,括号内各项都改变符号)去括号时要注意:1、 不要漏乘括号内的任何一项;2、若括号前面是“-”号,记住去括号后括号内各项都变号.习题训练:解方程,如课本P122练一练1,P113练一练2等.思维拓展,解简单的应用题,如课本P123练一练3或补充一些题,如含小括号、中括号、大括号的方程(这方面课本安排几乎没有,只限浅显问题,教师不必深究)

北师大初中七年级数学上册生活中的立体图形教案1
解析:此题作为一道开放型题,分类的方法非常多,只要能说明分类的理由即可.但要注意:按某一标准分类时,要做到不重不漏,分类标准不同时,分类的结果也就不尽相同.解:本题答案不唯一,如按柱体、锥体、球体分类:(2)(3)(5)和(6)都是柱体,(4)(7)是锥体,(1)是球体.方法总结:生活中常见几何体有两种分类:一种按柱体、锥体、球体分类;一种按平面和曲面分类.探究点二:几何体的形成笔尖画线可以理解为点动成线.使用数学知识解释下列生活中的现象:(1)流星划破夜空,留下美丽的弧线;(2)一条拉直的细线切开了一块豆腐;(3)把一枚硬币立在桌面上用力一转,形成一个球.解析:解释现象关键是看其属于什么运动.解:(1)点动成线;(2)线动成面;(3)面动成体.方法总结:生活中的很多现象都可以用数学知识来解释,关键是要找到生活实例与数学知识的连接点,如第(1)题可将流星看作一个点,则“点动成线”.如图所示,将平面图形绕轴旋转一周,得到的几何体是()

北师大初中七年级数学上册生活中的立体图形教案2
四、做一做(实践)1、用牙签和橡皮泥制作球体和一些柱体和锥体,看哪些同学做得比较标准。2、使出事先准备好的等边三角形纸片,试将它折成一个正四面体。五、试一试(探索)课前,发给学生阅读材料《晶体--自然界的多面体》,让学生通过阅读了解什么是正多面体,正多面体是柏拉图约在公元400年独立发现的,在这之前,埃及人已经用于建筑(埃及金字塔),以此激励学生探索的欲望。教师出示实物模型:正四面体、正方体、正八面体、正十二面体、正二十面体1、以正四面体为例,说出它的顶点数、棱数和面数。2、再让学生观察、讨论其它正多面体的顶点数、棱数和面数。将结果记入书上的P128的表格。引导学生发现结论。3、(延伸):若随意做一个多面体,看看是否还是那个结果。

北师大初中七年级数学上册探索与表达规律教案2
学习目标:1、知识与技能(1)会用字母、运算符号表示简单问题的规律,并能验证所探索的规律。(2)能综合所学知识解决实际问题和数学问题,发展学生应用数学的意识,培养学生的实践能力和创新意识。2、过程与方法(1)经历探索数量关系,运用符号表示规律,通过验算验证规律的过程。(2)在解决问题的过程中体验归纳、分析、猜想、抽象还有类比、转化等思维方法,发展学生抽象思维能力,培养学生良好的思维品质。3、情感、态度与价值观通过对实际问题中规律的探索,体验“从特殊到一般、再到特殊”的辩证思想,激发学生的探究热情和对数学的学习热情。学习重点:探索实际问题中蕴涵的关系和规律。学习难点:用字母、运算符号表示一般规律。学习过程:一、创景引入活动:出示一张月历,学生任意选出3×3方格框出的9个数,并计算出这9个数的和,告诉老师,老师就可以说出你所选的是哪9个数。

北师大初中七年级数学上册探索与表达规律教案1
(1)依照此规律,第20个图形共有几个五角星?(2)摆成第n个图形需要几个五角星?(3)摆成第2015个图形需要几个五角星?解析:通过观察已知图形可得:每个图形都比其前一个图形多3个五角星,根据此规律即可解答.解:(1)根据题意得,第1个图中,五角星有3个(3×1);第2个图中,五角星有6个(3×2);第3个图中,五角星有9个(3×3);第4个图中,五角星有12个(3×4);∴第n个图中有五角星3n个.∴第20个图中五角星有3×20=60个.(2)摆成第n个图形需要五角星3n个.(3)摆成第2015个图形需要6045个五角星.方法总结:此题首先要结合图形具体数出几个值,注意由特殊到一般的分析方法.此题的规律为摆成第n个图形需要3n个五角星.三、板书设计教学过程中,强调学生自主探索和合作交流,经历观察、操作、验证、归纳、分析、猜想、抽象、积累、类比、转化等思维过程,从中获得数学知识与技能,体验教学活动的方法,同时升华学生的情感态度和价值观.

北师大初中七年级数学上册统计图的选择教案1
(1)该校被抽查的学生共有多少名?(2)现规定视力5.1及以上为合格,若被抽查年级共有600名学生,估计该年级在2015年有多少名学生视力合格.解析:由折线统计图可知2015年被抽取的学生人数,且扇形统计图中对应的A区所占的百分比已知,由此即可求出被抽查的学生人数;根据扇形统计图中C、D区所占的百分比,即可求出该年级在2015年有多少名学生视力合格.解:(1)该校被抽查的学生人数为80÷40%=200(人);(2)估计该年级在2015年视力合格的学生人数为600×(10%+20%)=180(人).方法总结:本题的解题技巧在于从两个统计图中获取正确的信息,并互相补充互相利用.例如求被抽查的学生人数时,由折线统计图可知2015年被抽取的学生人数是80人,与其相对应的是扇形统计图中的A区,而A区所占的百分比是40%,由此求出被抽查的学生人数为80÷40%=200(人).

北师大初中七年级数学上册一元一次方程教案1
某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1儿童节”举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出x支,则依题意可列得的一元一次方程为( )A.1.2×0.8x+2×0.9(60+x)=87B.1.2×0.8x+2×0.9(60-x)=87C.2×0.9x+1.2×0.8(60+x)=87D.2×0.9x+1.2×0.8(60-x)=87解析:设铅笔卖出x支,根据“铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元”,得出等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87,据此列出方程为1.2×0.8x+2×0.9(60-x)=87.故选B.方法总结:解题的关键是读懂题意,设出未知数,找到题目当中的等量关系,最后列方程.三、板书设计教学过程中,通过对多种实际问题情境的分析,感受方程作为刻画现实世界有效模型的意义,通过观察、归纳一元一次方程的概念,使学生在分析实际问题情境的活动中体会数学与现实的密切联系.

北师大初中七年级数学上册应用一元一次方程——打折销售教案1
方法总结:让利10%,即利润为原来的90%.探究点三:求原价某商场节日酬宾:全场8折.一种电器在这次酬宾活动中的利润率为10%,它的进价为2000元,那么它的原价为多少元?解析:本题中的利润为(2000×10%)元,销售价为(原价×80%)元,根据公式建立起方程即可.解:设原价为x元,根据题意,得80%x-2000=2000×10%.解得x=2750.答:它的原价为2750元.方法总结:典例关系:售价=进价+利润,售价=原价×打折数×0.1,售价=进价×(1+利润率).三、板书设计本节课从和我们的生活息息相关的利润问题入手,让学生在具体情境中感受到数学在生活实际中的应用,从而激发他们学习数学的兴趣.根据“实际售价=进价+利润”等数量关系列一元一次方程解决与打折销售有关的实际问题.审清题意,找出等量关系是解决问题的关键.另外,商品经济问题的题型很多,让学生触类旁通,达到举一反三,灵活的运用有关的公式解决实际问题,提高学生的数学能力.



