-

镇2022年工作总结及2023年工作思路
(一)推进产业优化升级,综合经济实力进一步增强。工业经济稳进提质。今年以来,国内外环境复杂性不确定性剧,我镇立足家电制造产业基础,因地制宜、准确识变、把握机遇,在不稳定不确定中积极谋求增长,把快制造业新旧动能转换、推动产业转型升级作为高质量发展的着力点,扎实推进全域产业治理。1-9月规上实现产值50.91亿元,同比增长2.43。三产动能持续释放。利用零土地招商引资、慈企回归、产销分离等综合手段、超常规工作力度,招商引资1家380万美元(外资),招商引资3家,分离发展1家。1-9月批发商品销售额增速26.7,限上商品销售额增速12.9,零售业商品销售额增速9.3,住宿餐饮业营业额增速20,社会消品零售总额增速17.3,限下社零增速11.2,商务经济领域各项数据全面由负转正,实现历史性突破。现代农业发展壮大。巩固“两非”整治成果,立足“溪上稻乡”项目,高效推进优质水稻生产基地、精品盆景花卉基地、农旅会客厅等个子项目建设,完成640亩早稻、300亩单季稻、500亩高粱的种植。启动面积740亩的四界村旱改水耕地质量提升项目。占地面积3130.86亩的高标准农田建设项目完成开招标投标并进场施工。 (二)推进城乡规划建设,城镇综合功能进一步完善。完善基础设施配套。推进国土空间规划编制,划定“三区三线”,进一步挖掘城镇存量用地,通过盘活存量,做优增量,促进镇社会经济健康发展。镇2022年度农村生活污水纳管治理工程(四界村二期)立项启动。完成镇中心小学光伏板1500平方的安装。建设停车位24只,解决群停车难问题。奋力攻坚重点工程。积极推进市重点项目慈溪市曹娥江引水工程慈溪中部通道基础设施配套工程(洋浦至蛟门浦)的房屋征收拆迁工作,截至11月2日,集体土地房屋拆迁签约率达到38.96。同时谋划启动三塘横江两侧生活休闲、商住宜居区域的规划布局。强势推进三改一拆。拆除违章建筑52起,占地面积78356平方米、建筑面积90359平方米,土地利用面积为81369平方米。处置下发的重点违法建筑13处,建筑面积达到56743平方米。完成农村乱占耕地建房专项整治,共发现、制止、查处违法案件108起,面积达16226.78平方米,下发责令停止违法行为通知书90份、责令限期整改违法行为通知书72份。

镇2022年度工作总结和2023年工作思路
一、主要工作开展情况 1、聚焦稳进提质,发展动能持续增强。一是狠抓平台建设。紧抓国土空间规划契机,强化镇工业东区、西区、北区及农业园区四个区产业发展空间优化拓展,稳步推进大河门山塘地块、榨菜整治提升产业园区、复线北侧地块四等相关工作,谋深谋实大河门山塘地块产业集聚区建设,完成采矿权拍卖亿元,着力拓展产业平台承载力。持续推进低效用地和园区二次开发利用,今年已盘活三和、世亚、华孚等处闲置厂房及用地,腾出空间约亩。二是狠抓项目建设。强力推进总投资亿元的容百锂电项目(目前容百-标段完成试生产,已进入投料试生产阶段),紧盯总投资亿元的松石、朗亿、柯仕等个在建项目,快复线北侧地块招商项目落地,截止月,我镇已完成宁波市外实到内资万元,市外实到内资万元,浙商创业创新实到资金完成元。大力推进“零土地”指标的增资扩产项目,切实提高土地容积率,提升亩均效益,目前瑞华、保世洁、珂仕二期等工业基建项目已基本完工。三是狠抓转型升级。深入开展稳链纾困助企活动,引导和鼓励企业练内功、拓市场、优布局,着力推动企业大技改投入,快企业智能化改造,完成企业高新企业培育入库家,高新申报家,宁波科技型中小企业备案家,国家科技型中小企业完成评价家。实现高新技术产业增值亿元,同比增长。四是狠抓特色农业。以味香园葡萄专业合作社为引领,充分打响打好“味香园”葡萄品牌,目前味香园葡萄品牌价值已达亿元人民币。持续深化农旅融合,以“()江南葡萄节”为活动载体,积极拓展“直播带货”、“夜市经济”等销售推广渠道,全年葡萄采摘游客达到万人次以上,经济效益超亿元。 2、聚焦全域提升,城乡品质持续优化。一是城镇品质巩固提升。深入开展“精特亮”创建,总投资万元“果香姚北”乡村明线段顺利完工。全力开展“拆违治乱”百日攻坚行动,处置违章宗,拆除面积万平方米,并以“白+黑”、“5+2”之势攻坚完成国土变调查问题销整改近亩。集中力量推进N连接线土地征用及房屋拆迁工作,实现房屋拆迁“清零”,完成征地签约率。持续推进老街立面改造及历史风貌建筑修缮,今年共完成户民居仿古改造,投入资金约万元。二是美丽乡村优化升级。以邵家丘村“未来乡村”建设为引领,深入开展兰海、临海、临浦等个村“精特亮”创建工程及村新时代美丽乡村梳理式改造,抓牢全域土地整治“一村一策”主攻方向,截止目前已为村级集体经济减少债务余万元。着力深化“一扫七治”、明村镇创建整改、垃圾分类等工作,深入开展农村环境“大清理、大起底”综合整治百日攻坚行动,逗硬整治人居环境突出问题。三是生态环境持续改善。快镇域范围内污水管网建设,省级“污水零直排区”创建、工业西区“污水零直排区”创建通过验收,北区省创、东区县创快推进。持续深化“五水共治”,重点实施大浦江水质提升工程,做好大浦江宁波生态补偿考核断面Ⅲ类水质达标及七塘横江段“甬有碧水”考核任务。成功创建国家卫生镇,探索实施全域保洁一体化。推进投资万元的生活垃圾填埋场处置项目,预计月底全部完工,年底前销。

乡2023年工作总结和2024年工作思路
三、2024年工作思路(一)深耕不辍服务保障。紧紧围绕偏远山区“一老一少”现实需求,持续深化“共富食堂”品牌,继续盘活社会慈善力量,壮大基本兜底资金盘。延伸服务范围,探索偏远自然村“邻里和睦互助点”的运行,持续推进留守学生“营养餐”工程,真正将“一老一少”的需求解决在实际问题上。(二)高质发展农业产业。利用本乡17.4万亩的山场优势,盘活乡林场资源,在现有的高山红薯、油茶、谷精草等基地基础上提质扩面,真正形成相对完善的产业链条,打造“XX红”系列农业品牌,实现群众在家门口增收;(三)全力推进环境治理。抓好环境治理和生态保护,全面推进全域环境综合整治,提升人居环境。秉承“一村一品”建设目标,推进环境整治,狠抓生态保护工作,探索森林消防长效机制,确保楠溪江源头生态绝对安全。以溪界公路生态景观带打造、建成区风貌整治工程等改造行动为抓手,项目化推进宜居、宜业、宜游的美丽乡村建设,助推“浙”里乡村奔向共富共美“嘉”生活。

2023年工作总结和2024年工作思路
加强区域餐饮食品安全基础保障能力体制机制建设,针对疫情期间餐饮保供所暴露出的应急机制缺失、协同处置缺位等问题,将各基础能力要素集成进行数字赋能,探索打造全新全域餐饮食品安全保供系统应用,构建“组织机制协调顺畅”、“法定职责责任明确”、“制度流程设计清晰”、“部门监管协同高效”、“食品安全保供精准”、“专业技术支撑有力”等六大功能模块,切实加强平时“专业化监管、跨部门协作、社会化共治”等三大能力建设,确保重大活动保障、突发公共事件,餐饮保供随时能“拉得出、打得赢”。持续推进星级农村食品经营示范店建设,完善并推广农村食品监管数字化模型,力争在农村食品安全监管上精准破题。全面推进两个“规定”落实,建立两证和强标类工业产品生产和销售单位质量安全档案,督促企业健全质量管理相关制度。发挥部门优势,做好新开工大型项目的特种设备服务工作,变“事后监督”为“事前服务”,为企业建设及后续安全使用管理打下坚实基础。

XX镇2023年工作总结及2024年工作安排
(1)聚力提升城乡生活品质。加快改善全镇群众生产生活用水条件,争取集镇用上青山水。加快陆水河三期沿河步道项目实施进度,整治河道岸线景观,为全镇群众再添休闲新去处。配合中建二局,加快通修高速公路XX段建设施工进度。不断加大水、土、林生态治理力度,努力实现河长制、林长制长效长治。加快集镇弱电入地、污水管网改造等施工进度。(2)聚力扩大优势产业规模。依托茶叶、水果种植等传统优势,扩大种植面积,丰富种植品种,以品牌和渠道为重点,提升规范化、标准化管理水平;发挥万亩林地优势,大力推进林下经济发展规模。加快1200亩枫芊鸣绿色生态产业园区建设进度,在开拓中药材产业领域和做长产业链条上下功夫。举办菊花节,提升XX菊花品牌的影响力和知名度,推动菊花等中药材产业和乡村旅游产业的有机融合和快速发展。

街道2023年工作总结和2024年工作思路
6.提升应急能力,安全生产形势向好。时刻做到严守安全生产工作底线,建立班子成员带队实地巡查制度,不断压实安全生产责任,代表鹤城接受省、市多轮检查,工作成效获上级肯定。商贸领域和重点企业方面,完成辖区英泰国际重大安全隐患整改,紧盯步步高、通程、国际商贸城等综合体安全生产工作,加强中民燃气等重点企业安全生产隐患排查,服务辖区经济社会高质量发展。民生领域方面,针对辖区消防出警中老旧小区用电起火比例较高特点,联合国网鹤城供电公司开展无物管小区用电安全隐患专项大排查,排查用电安全隐患130余处,纳入省国网隐患整改项目。完成瑞丰园等2个小区“一户一表”改造试点。持续开展燃气安全整治,联合中民、新奥燃气公司对辖区400余家餐饮门店燃气安全进行全覆盖、多频次的排查整治。建筑领域方面,完成经营性自建房排查整治工作,其中7栋鉴定为C级的住房和1栋D级住房均整治到位。对辖区在建工地进行常态化安全巡查,发现问题及时交办并督促整改。二、存在的主要问题

药品医疗器械化妆品稽查工作总结附药品案件查办有关情况统计表
一、整体情况(一)案件查办总体情况1.案件数量情况:2022年1-7月份药化械案件10件,同比增长900%。其中药品类案件2件,同比增长100%,医疗器械类案件3件,化妆品类案件5件。药品类案件中使用《中华人民共和国药品管理法》的规定予以处罚的案件有1件,使用《药品流通监督管理办法》予以行政处罚的案件有1件。3件医疗器械类案件涉案产品都是未经注册、无合格证明文件的医用口罩。2.行政处罚情况:2022年1-7月份药品类案件2件,给予财产罚的案件2件,同比增长100%;医疗器械类案件3件,给予财产罚的案件3件;化妆品类案件5件,其中给予财产罚的案件4件,给予名誉罚的案件1件。(二)药品医疗器械化妆品案件查办重点情况1.药品案件:2022年1月-7月,本辖区共查处2家药品经营单位,其中1家存在拆零药品包装上无有效期的行为,使用新的《中华人民共和国药品管理法》给予当事人警告。2.医疗器械案件:2022年1月-7月,本辖区共查处3家医疗器械经营单位,3家违法单位的涉案产品均为医用口罩。

售货合同
买卖双方同意按下列条款由买方购进,由卖方出售下列商品,订立本合同:1. 品名及规格 数量 单价 总价2.合同总值: 3.包 装: 4.保 险:由卖方按发票金额110%投保。5.唛 头: 6.装运口岸: 7.目的口岸: 8.装运期限: 9.付款条件;买方应通过买卖双方同意的银行,开立以卖方为受益人的、不可撤销的、可转让和分割的信用证。该信用证凭装运单据在 银行见单即付。该信用证必须在 前开到卖方。信用证有效期为装船后15天在 到期。10.装运单据:卖方应提供下列单据。(1)已装船清洁提单;(2)发票;(3)装箱单;(4)保险单。11.装运条件:

焦作市“八五”普法工作综述
专业化推进公益普法。市县两级司法行政部门均配备普法依法治理工作专职工作队伍,全市107个基层司法所、56个律师事务所、29个基层法律服务所以及5400余名人民调解员,11223名“法律明白人”都担负着法治宣传任务。组建“八五普法讲师团”“重大工程项目律师服务团”“工会法律服务律师团”“市检察院师资人才库”“教育系统普法讲师团”等多个专业法律服务团,推进法律专业人才参与普法实践。全市各县(市、区)、各行业、各单位都成立了本系统的普法志愿者队伍,定期开展普法志愿活动,全市4000多名普法志愿者长年活跃在基层,成为推动传播法治声音的重要力量。数字化打造普法品牌。利用新媒体新技术开展精准普法。积极打造集微信、微博、“今日头条”客户端、官方网站“四位一体”的政务公开普法新平台,市、县两级司法局全部建成了官网、微博、微信、手机报四大普法平台,全市各单位、部门(行业)共开通普法微博、微信公众服务号、手机APP1000多个。

2022年度工会工作总结
2、加强法律法规等教育。利用请进来、派下去等办法进行业务、法律、法规、心理学、安全生产等知识培训。一是邀请市总工会领导上课,一期授训120多人;二是利用全国总工会女工部派下来的心理学专家到村、企业上课,六期受训560人;三是利用新建工会召开职工代表大会之际上安全生产课,八期受训250人;四是与团工委等联合开展了“综治进民企”知识竞赛,与安监所等联合开展了“安全知识”竞赛。此外,各村、企业工会结合本单位实际,3、加强职能技能教育。一是街道工会与经发办等有关部门组织开展了两次消防演习,观摩人数达250人次;二是各工会广泛开展“学技术、比技能”为主要内容的操作运动会,金轮集团工会从6月份开始在各分厂开展了初赛,参与项目15个,参与人数达520人;集团工会打算于九月份进行决赛。

国企工会2023年工作总结
(二)开展主题活动,激发职工建功立业热情。紧扣高质量发展主线,结合行业实际,依托职工之家工作室,实施建功新时代主力军行动,开展技能比武、职工创新和班组竞赛,激励和引导职工争做技术能手、安全标兵、劳动模范。(三)做实关心关爱,提升职工幸福感获得感安全感。关心职工生活,开展多种形式的慰问走访工作,维护好职工的合法权益,以更有效的服务回应职工呼声。深化“安康杯”竞赛等群众性安全生产工作,切实维护职工群众安全健康权益。扎实做好风险隐患排查化解工作,切实维护劳动领域政治安全、维护职工队伍和工会组织的团结统一,积极推进建设更高水平的工会建设。(四)紧紧围绕中心工作,推动工会整体工作上台阶。围绕中心工作,加强阵地建设和管理,不断提高协调服务能力和水平,密切关注职工思想动向,做好新闻宣传的组织策划,讲好工会故事、职工故事,传播职工声音。积极探索工会工作的新方法,力争开展一些引领风尚、高层次、有品位、有特色的活动,推动工会工作增能力提水平上台阶。

【高教版】中职数学基础模块上册:2.1《不等式的基本性质》教案设计
教师姓名 课程名称数学班 级 授课日期 授课顺序 章节名称§2.1 不等式的基本性质教 学 目 标知识目标:1、理解不等式的概念 2、掌握不等式的基本性质 技能目标:1、会比较两个数的大小 2、会用做差法比较两个整式的大小 情感目标:体会不等式在日常生活中的应用,感受数学的有用性教学 重点 和 难点 重点: 不等式的概念和基本性质 难点: 1、会比较两个整式的大小 2、能根据应用题的表述,列出相应的表达式教 学 资 源《数学》(第一册) 多媒体课件评 估 反 馈课堂提问 课堂练习作 业习题2.1课后记
【高教版】中职数学基础模块上册:2.3《一元二次不等式》教案设计
教师姓名 课程名称数学班 级 授课日期 授课顺序 章节名称§2.3 一元二次不等式教 学 目 标知识目标:1、理解一元二次不等式和一元二次方程以及二次函数之间的关系 2、理解一元二次不等式的解集的含义 3、一元二次不等式的解集与二次函数图像的对应 技能目标:1、会解一元二次方程 2、会画二次函数的图像 3、能结合图像写出一元二次不等式的解集 情感目标:体会知识之间的相互关联性,体会数形结合思想的重要性教学 重点 和 难点重点: 1、一元二次不等式的解集的含义 2、一元二次不等式与二次函数的关系 难点: 1、将一元二次不等式和一元二次方程以及二次函数联系起来 2、在函数图像上正确的找到解集对应的部分教 学 资 源《数学》(第一册) 多媒体课件评 估 反 馈课堂提问 课堂练习作 业习题2.3课后记本节课内容是比较重要的,是一元二次方程、一元二次函数、一元二次不等式的结合,相关知识点融会贯通,数形结合的思想方法在这有很好的运用。三种情况只要讲清楚一种,另外两种可由学生自行推出结论。
【高教版】中职数学基础模块上册:2.4《含绝对值的不等式》教案设计
教师姓名 课程名称数学班 级 授课日期 授课顺序 章节名称§2.4 含绝对值的不等式教 学 目 标知识目标:1、理解绝对值的几何意义 2、掌握简单的含绝对值不等式的解法 3、掌握含绝对值不等式的等价形式 技能目标:1、会解形如|ax+b|>c或|ax+b|<c的绝对值不等式 情感目标:通过学习,体会数形结合、整体代换及等价转换的数学思想方法教学 重点 和 难点重点: 1、绝对值的几何意义 2、基本绝对值不等式|x|>a或|x|<a的解 难点: 1、去绝对值符号后不等式与原不等式保持等价性教 学 资 源《数学》(第一册) 多媒体课件评 估 反 馈课堂提问 课堂练习作 业习题2.4课后记不等式的基本性质是初中就学习过的内容,分式不等式的解法是哦本节课的一个重点和难点,尤其是不等号另一边不为0的情况,需要移项,这一点在强调前学生考虑不到,因此解题错误多。区间是个新内容,学生往往将连续的正数写作一个区间,这是常见的错误,要进行提醒。另外,在均值不等式这里稍微补充了一些内容,引起学生的兴趣。

【高教版】中职数学基础模块上册:3.3《函数的实际应用举例》教学设计
课程分析中专数学课程教学是专业建设与专业课程体系改革的一部分,应与专业课教学融为一体,立足于为专业课服务,解决实际生活中常见问题,结合中专学生的实际,强调数学的应用性,以满足学生在今后的工作岗位上的实际应用为主,这也体现了新课标中突出应用性的理念。分段函数的实际应用在本课程中的地位:(1) 函数是中专数学学习的重点和难点,函数的思想贯穿于整个中专数学之中,分段函数在科技和生活的各个领域有着十分广泛的应用。(2) 本节所探讨学习分段函数在生活生产中的实际问题上应用,培养学生分析与解决问题的能力,养成正确的数学化理性思维的同时,形成一种意识,即数学“源于生活、寓于生活、用于生活”。教材分析 教材使用的是中等职业教育课程改革国家规划教材,依照13级教学计划,函数的实际应用举例内容安排在第三章函数的最后一部分讲解。本节内容是在学生熟知函数的概念,表示方法和对函数性质有一定了解的基础上研究分段函数,同时深化学生对函数概念的理解和认识,也为接下来学习指数函数和对数函数作了良好铺垫。根据13级学生实际情况,由生活生产中的实际问题入手,求得分段函数此部分知识以学生生活常识为背景,可以引导学生分析得出。
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点*巩固知识 典型例题 例6 一艘船以每小时36海里的速度向正北方向航行(如图1-9).在A处观察到灯塔C在船的北偏东方向,小时后船行驶到B处,此时灯塔C在船的北偏东方向,求B处和灯塔C的距离(精确到0.1海里). 图1-9 A 解因为∠NBC=,A=,所以.由题意知 (海里). 由正弦定理得 (海里). 答:B处离灯塔约为海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和(图1-10),在平地上选择适合测量的点C,如果,m,m,试计算隧道AB的长度(精确到m). 图1-10 解 在ABC中,由余弦定理知 =. 所以 m. 答:隧道AB的长度约为409m. 例8 三个力作用于一点O(如图1-11)并且处于平衡状态,已知的大小分别为100N,120N,的夹角是60°,求F的大小(精确到1N)和方向. 图1-11 解 由向量加法的平行四边形法则知,向量表示F1,F2的合力F合,由力的平衡原理知,F应在的反向延长线上,且大小与F合相等. 在△OAC中,∠OAC=180°60°=120°,OA=100, AC=OB=120,由余弦定理得 OC= = ≈191(N). 在△AOC中,由正弦定理,得 sin∠AOC=≈0.5441, 所以∠AOC≈33°,F与F1间的夹角是180°–33°=147°. 答:F约为191N,F与F合的方向相反,且与F1的夹角约为147°. 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点
【高教版】中职数学拓展模块:1.2《正弦型函数》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.2正弦型函数. *创设情境 兴趣导入 与正弦函数图像的做法类似,可以用“五点法”作出正弦型函数的图像.正弦型函数的图像叫做正弦型曲线. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 5*巩固知识 典型例题 例3 作出函数在一个周期内的简图. 分析 函数与函数的周期都是,最大值都是2,最小值都是-2. 解 为求出图像上五个关键点的横坐标,分别令,,,,,求出对应的值与函数的值,列表1-1如下: 表 001000200 以表中每组的值为坐标,描出对应五个关键点(,0)、(,2)、(,0)、(,?2)、(,0).用光滑的曲线联结各点,得到函数在一个周期内的图像(如图). 图 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 15
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教学设计
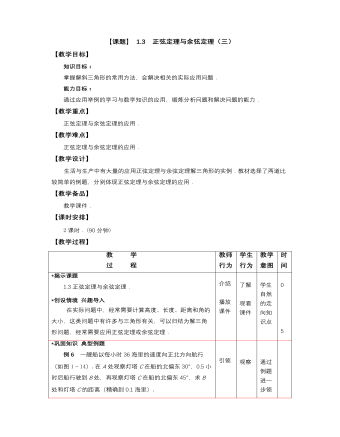
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题,经常需要应用正弦定理或余弦定理. 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行(如图1-14).在A处观察灯塔C在船的北偏东30°,0.5小时后船行驶到B处,再观察灯塔C在船的北偏东45°,求B处和灯塔C的距离(精确到0.1海里). 解 因为∠NBC=45°,A=30°,所以C=15°, AB = 36×0.5 = 18 (海里). 由正弦定理得 答:B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和B(图1-15),在平地上选择适合测量的点C,如果C=60°,AB = 350m,BC = 450m,试计算隧道AB的长度(精确到1m). 解 在△ABC中,由余弦定理知 =167500. 所以AB≈409m. 答:隧道AB的长度约为409m. 图1-15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

【高教版】中职数学拓展模块:3.1《排列与组合》优秀教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 3.1 排列与组合. *创设情境 兴趣导入 基础模块中,曾经学习了两个计数原理.大家知道: (1)如果完成一件事,有N类方式.第一类方式有k1种方法,第二类方式有k2种方法,……,第n类方式有kn种方法,那么完成这件事的方法共有 = + +…+(种). (3.1) (2)如果完成一件事,需要分成N个步骤.完成第1个步骤有k1种方法,完成第2个步骤有k2种方法,……,完成第n个步骤有kn种方法,并且只有这n个步骤都完成后,这件事才能完成,那么完成这件事的方法共有 = · ·…·(种). (3.2) 下面看一个问题: 在北京、重庆、上海3个民航站之间的直达航线,需要准备多少种不同的机票? 这个问题就是从北京、重庆、上海3个民航站中,每次取出2个站,按照起点在前,终点在后的顺序排列,求不同的排列方法的总数. 首先确定机票的起点,从3个民航站中任意选取1个,有3种不同的方法;然后确定机票的终点,从剩余的2个民航站中任意选取1个,有2种不同的方法.根据分步计数原理,共有3×2=6种不同的方法,即需要准备6种不同的飞机票: 北京→重庆,北京→上海,重庆→北京,重庆→上海,上海→北京,上海→重庆. 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 15*动脑思考 探索新知 我们将被取的对象(如上面问题中的民航站)叫做元素,上面的问题就是:从3个不同元素中,任取2个,按照一定的顺序排成一列,可以得到多少种不同的排列. 一般地,从n个不同元素中,任取m (m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,时叫做选排列,时叫做全排列. 总结 归纳 分析 关键 词语 思考 理解 记忆 引导学生发现解决问题方法 20

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.





