-

学生学习《未成年人保护法》心得体会参考范文
孩子们是国家的未来祖国的希望,我们对他们的合法权给予特殊呵护,也是一项具有挑站性的工作,这需要全社会共同参与到其中,我们每一个人一起完成,共同维护未成年人合法权益,更好的履行自己的责任和义务,让孩子们活泼健康快乐的成长,成为一代强人,将来为祖国做出更大的贡献。

幼教大班数学教案-学习2—9的相邻数
2、让幼儿熟练地找出2—9个数的相邻数。3、进行朋友间团结友爱的教育。活动准备:1、1— 10的数字头饰一套,1—10的数字卡一套。2、已学会10以内的数字。活动过程:一、开始部分:师:小朋友,我们知道每个数子都有自己的邻居,前面一个,后面一个,前面的比它少1,后面的比它多1。今天,我们来做个游戏,看谁能快速的找出数字的邻居。

关于开展教师师风师德学习心得体会例文
一、具体实施方面: 1、根据区教文体局要求,组织全体教职工集中学习《教育法》、《教师法》、《未成年人保护法》、《中小学教师职业道德规范》、《郑州市中小学教师职业道德建设十项规范、十项惩戒》、《职业道德考核办法》等相关法律法规,并认真做好记录,写出深刻的反思和总结。 2、学习师德标兵的优秀事迹,让每位教师把纲要、规范、师德模范作为一面镜子,深刻反思自己的言行举止,深化师德教育。通过学习,提高全体教职工对加强师德师风建设的重要性、必要性的认识,自觉规范从教行为,促进园风、教风、学风的形成。

幼儿教师安全培训学习心得体会范文四篇
新到XX有限责任公司的第二天(7月2日)公司就组织我们新来的八名员工参加了为时24学时的入职安全培训。本公司的主要产品有尿素、复合肥等,其原料有氨、硫酸等,生产环境存在高温高压、有毒有害、易腐蚀这些安全隐患,所以我认为这次安全培训对我们来说是很有必要的。 这次培训的地点是在科技楼二楼的会议室,培训人是安全环保部的周老师,周老师语言幽默、知识丰富,对公司的安全状况可谓了如指掌,首先他给我们介绍了公司的安全文化理念即“生命第一,安全第一,尊重生命,共创平安”以及公司往年发生的一些安全事故案例,让我们明白安全问题就在我们身边。然后介绍了复合肥生产的基本流程,主要说明其间可能存在的安全问题。再然后解读了生产操作的一些禁止条令和安全守则。最后就是消防措施的讲解:火灾爆炸事故是如何发生的,遇到了该怎么处理等等。 通过这次安全培训,我认识到了安全的重要性,特别是化肥公司的安全更是重要。同时我还学到了很多的安全知识,比如进入生产区一定要穿防腐工作服,戴防毒面具等等。生产离不开安全,安全在任何生产单位都是第一位的,安全问题是一个永不过时的话题,关于怎样做到安全,我觉得首先一定要有安全意识,时刻不忘安全才能有效及时地发现安全隐患。另外就是预防为主,明确岗位所有操作可能存在的隐患,做好防范措施,尽量避免安全事故的发生。最后我们要严格遵守公司劳动纪律及有关安全规定,严格要求自己,从自己做起,然后推及他人,争做美丰劳动模范。

幼儿园中班数学教案:学习4的加减法
2、独立将三幅图连起来,表达其中的含义,运用正确的词汇表达图意。 3、敢于克服胆怯的心理,大胆回答问题。活动准备:1、教具:有关4的减法图三幅。 2、学具:幼儿用书,铅笔。活动过程:1、集体活动。 (1)游戏“看谁说得快”。 教师提出要与幼儿玩游戏,随后讲一讲游戏规则:教师说一个数字,请幼儿说出它后面的一个数字。教师报数,全体幼儿尝试回答,当全体幼儿玩的比较熟练后,可以与小组的幼儿玩。 教师说出游戏的另一个规则:教师说一个数字,幼儿说出它前面的一个数字。教师报数,全体幼儿尝试回答。

大班数学教案:学习8的第一、二组加减(江苏)
2、探索根据实物图的内容选择答案图,并列出8的第一、二组加减算试。3、用较准确、完整的语言讲述算式的含意。教学准备:教具:图片:8的第一组实物图七张、第二组实物图五张。学具:幼儿用书、铅笔若干。操作材料若干(7以内的加减算式和8的第一、二组加减算试。)活动过程:一、集体活动。1、复习8的组成——玩碰球游戏。2、学习8的第一组加减。

大班数学教案:电话号码学习6以内的数
活动准备:电话本,!—6的数字卡活动过程:一,用打电话的方式,列出不同数字的排序1, 小动物要开运动会了,我们怎么才能通知他们呢?2, 打电话要知道电话号码,我们来查一查,小动物家的电话号码是多少?3, 这么多的电话号码哪些地方是一样的?4, 都有5个数字,为什么电话号码是不一样的呢?小结:相同的几个数字,经过不同的排列,就会有不同的电话号码,真有趣!

关于个人学习家庭教育心得感悟与感受八篇
孩子做了错事,父母不可听之任之,一定要认真处理。必须向孩子严厉指出:什么是应该做的,什么是不能去做的,并要根据孩子错误情节的严重性给予必要的惩罚,让孩子体验到做错事后所引起的不愉快,从而牢记教训。对孩子故意的破坏性错误不能任其发展下去,要认识到孩子的不良习惯不是一天、两天形成的,所以教育也需要一个较长过程,不能性急,帮助孩子逐步明白道理,学会自尊、自律。例如对于孩子某些不良行为,父母可通过施予孩子不愉快的非语言刺激,来减少和控制孩子不良行为的频率,比如:目光注视(以冷峻的目光较长时间的注视孩子)、距离控制(逼近或远离孩子)、轻微的惩罚(拿走孩子喜爱的物品),这样会使孩子对自己的错误行为产生内疚和羞愧,从而减少和消除不良行为发生的次数。

在2023年关于学习贯彻主题教育的点评总结讲话
同时,要结合整改做好“预防文章”,突出抓早抓小,完善各项规章制度,把纪律挺在前面,强化制度的刚性约束,切实把专题学习贯彻新时代中国特色社会主义思想ZT教育的成果转化为指导工作实践的有力武器。三是严守纪律规矩,保持勤政廉洁。身边的反面典型就是最好的警示,大家要深刻汲取XX严重违纪违法案件教训,深刻认识到失责必问、问责必严已经成为常态。要坚决扛起全面从严治D的政治责任,严格落实“一岗双责”,营造风清气正的政治生态。要牢固树立法纪意识,严守政治纪律和政治规矩。要树立正确的权力观、政绩观、事业观,严把小事、守好小节,管好家人、树好家风,远离“圈子”、防止“围猎”,始终做到崇廉拒腐,干净做事。最后,希望XX班子团结带领XXD员干部群众坚持发展为先、实干为要,紧盯目标任务,奋力比学赶超,积极争先进位,有序推进年度各项工作,交出一份优异的答卷。

【高教版】中职数学基础模块上册:3.2《函数的性质》优秀教案
【教学目标】知识目标:⑴ 理解函数的单调性与奇偶性的概念;⑵ 会借助于函数图像讨论函数的单调性;⑶理解具有奇偶性的函数的图像特征,会判断简单函数的奇偶性.能力目标:⑴ 通过利用函数图像研究函数性质,培养学生的观察能力;⑵ 通过函数奇偶性的判断,培养学生的数学思维能力.【教学重点】⑴ 函数单调性与奇偶性的概念及其图像特征;⑵ 简单函数奇偶性的判定.【教学难点】函数奇偶性的判断.(*函数单调性的判断)【教学设计】(1)用学生熟悉的主题活动将所学的知识有机的整合在一起;(2)引导学生去感知数学的数形结合思想.通过图形认识特征,由此定义性质,再利用图形(或定义)进行性质的判断;(3)在问题的思考、交流、解决中培养和发展学生的思维能力.【教学备品】教学课件.【课时安排】3课时.(90分钟)【教学过程】

【高教版】中职数学基础模块上册:5.6《三角函数的图像和性质》优秀教案
创设情景 兴趣导入问题 观察钟表,如果当前的时间是2点,那么时针走过12个小时后,显示的时间是多少呢?再经过12个小时后,显示的时间是多少呢?.解决每间隔12小时,当前时间2点重复出现.推广类似这样的周期现象还有哪些? 动脑思考 探索新知概念 对于函数,如果存在一个不为零的常数,当取定义域内的每一个值时,都有,并且等式成立,那么,函数叫做周期函数,常数叫做这个函数的一个周期. 由于正弦函数的定义域是实数集R,对,恒有,并且,因此正弦函数是周期函数,并且 ,, ,及,,都是它的周期.通常把周期中最小的正数叫做最小正周期,简称周期,仍用表示.今后我们所研究的函数周期,都是指最小正周期.因此,正弦函数的周期是.

人教版新课标小学数学一年级上册1~5的加减法综合练习 说课稿
在组织教学和设计习题时,我考虑到了以下几点。1.培养“主角”意识,人人参与,人人提高。新理念下倡导自主学习,学生是学习的主人。本节课始终是学生在自主地解决问题、发现问题、解决问题。在教师的合作下,学生利用已有的知识经验,积极思维,提高了他们的分析综合能力,帮助他们掌握了解决数学问题的规律。同时,我力求让每个学生都体会到学习数学的快乐,在练习中,通过用手指表示得数,将式子列在自己的纸板上,小组交流,抢答等形式,让每个学生都动起来,都得到需要的数学知识。2.知识前后联系,融会贯通。在习题练习中,我注意多元化、开放化,需要学生将知识进行综合内化,来解决问题,这也是一种数学素养。比如决定上几号车厢,必须进行计算──统计──比较的思维活动;野生动物园情境列式中需选择条件,留有充分的思考空间;“海洋公园”情境中学生又初步有了两步计算的意念。3.充分利用小组合作学习的优势。

【高教版】中职数学基础模块上册:1.3《集合的运算》优秀教案
集合的基本运算(1) 一、教学目标 1、 知识与技能 (1)理解并集和交集的含义,会求两个简单集合的交集与并集。 (2)能够使用Venn图表达两个集合的运算,体会直观图像对抽象概念理解的作用。 2、过程与方法 (1)进一步体会类比的作用 。 (2) 进一步树立数形结合的思想。 3、情感态度与价值观 集合作为一种数学语言,让学生体会数学符号化表示问题的简洁美。 二、教学重点与难点 教学重点:并集与交集的含义 。 教学难点:理解并集与交集的概念,符号之间的区别与联系。

【高教版】中职数学基础模块上册:1.1《集合的概念》优秀教案
【课题】1.1 集合的概念【教学目标】1、理解集合、元素的概念及其关系,掌握常用数集的字母表示;2、掌握集合的列举法与描述法,会用适当的方法表示集合.3、通过集合语言的学习与运用,培养分类思维和有序思维,从而提升数学思维能力.4、接受集合语言,经历利用集合语言描述元素与集合间关系的过程,养成规范意识,发展严谨的作风。【教学重点】集合的表示法. 【教学难点】集合表示法的选择与规范书写.【教学设计】(1)通过生活中的实例导入集合与元素的概念;(2)引导学生自然地认识集合与元素的关系;(3)针对集合不同情况,认识到可以用列举和描述两种方法表示集合,然后再对表示法进行对比分析,完成知识的升华;(4)通过练习,巩固知识.(5)依照学生的认知规律,顺应学生的学习思路展开,自然地层层推进教学.

【高教版】中职数学基础模块上册:1.2《集合之间的关系》优秀教案
学科数学 课 题 1.2 集合之间的关系班级 人数 授课时数2 课 型新课 周次 授课时间 教 学 目 的 知识目标:(1)掌握子集、真子集的概念; (2)掌握两个集合相等的概念; (3)会判断集合之间的关系. 能力目标:培养学生的分析问题能力解决问题的能力. 情感目标:通过师生互动,学生之间的讨论分析,加强合作意识。 教学重点集合与集合间的关系及其相关符号表示. 教学难点真子集概念的理解.

北师大初中七年级数学上册多边形和圆的初步认识教案2
1、 如图4-25,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流2、 画一个半径是2cm的圆,并在其中画一个圆心为60º的扇形,你会计算这个扇形的面积吗?与同伴交流。教师对答案进行汇总,讲解本题解题思路:1、 因为一个圆被分成了大小相同的扇形,所以每个扇形的圆心角相同,又因为圆周角是360º,所以每个扇形的圆心角是360º÷3=120º,每个扇形的面积为整个圆的面积的三分之一。2、 先求出这个圆的面积S=πR²=4π,60÷360=1/6扇形面积=4π×1/6=2π/3【设计意图】运用小组合作交流的方式,既培养了学生的合作意识和能力,又达到了互帮互助以弱带强的目的,使学习比较吃力的同学也能参与到学习中来,体现了学生是学习的主体。
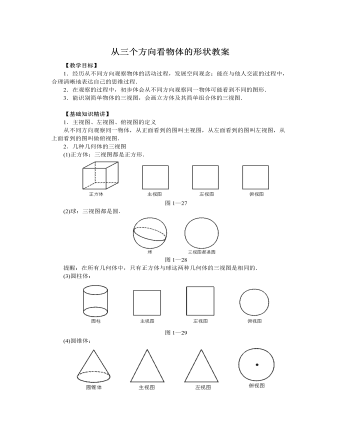
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

北师大初中七年级数学上册代数式的求值教案1
(1)请你用代数式表示水渠的横断面面积;(2)计算当a=3,b=1时,水渠的横断面面积.解析:(1)根据梯形面积=12(上底+下底)×高,即可用含有a、b的代数式表示水渠横断面面积;(2)把a=3、b=1带入到(1)中求出的代数式中,其结果即为水渠的横断面面积.解:(1)∵梯形面积=12(上底+下底)×高,∴水渠的横断面面积为:12(a+b)b(m2);(2)当a=3,b=1时水渠的横断面面积为12(3+1)×1=2(m2).方法总结:解答本题时需搞清下列几个问题:(1)题目中给出的是什么图形?(2)这种图形的面积公式是什么?(3)根据公式求图形的面积需要知道哪几个量?(4)这些量是否已知或能求出?搞清楚了这些问题,求解就水到渠成.三、板书设计教学过程中,应通过活动使学生感知代数式运算在判断和推理上的意义,增强学生学习数学的兴趣,培养学生积极的情感和态度,为进一步学习奠定坚实的基础.
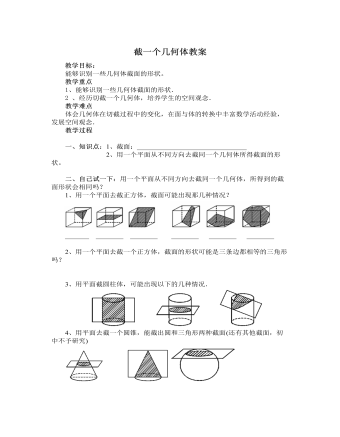
北师大初中七年级数学上册截一个几何体教案2
[例3]、用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是_________。四、巩固强化:1、一个正方体的截面不可能是( )A、三角形 B、梯形 C、五边形 D、七边形2、用一个平面去截五棱柱,边数最多的截面是_______形.3*、用一个平面去截几何体,若截面是三角形,这个几何体可能是__________________________________________________.4*、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如虹截面是三角形呢?5*、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?6*、几何体中的圆台、棱锥都是课外介绍的,所以我们就在这个栏目里继续为大家介绍这两种几何体的截面.(1)圆台用平面截圆台,截面形状会有_____和_______这两种较特殊图形,截法如下:

北师大初中七年级数学上册应用一元一次方程——打折销售教案1
方法总结:让利10%,即利润为原来的90%.探究点三:求原价某商场节日酬宾:全场8折.一种电器在这次酬宾活动中的利润率为10%,它的进价为2000元,那么它的原价为多少元?解析:本题中的利润为(2000×10%)元,销售价为(原价×80%)元,根据公式建立起方程即可.解:设原价为x元,根据题意,得80%x-2000=2000×10%.解得x=2750.答:它的原价为2750元.方法总结:典例关系:售价=进价+利润,售价=原价×打折数×0.1,售价=进价×(1+利润率).三、板书设计本节课从和我们的生活息息相关的利润问题入手,让学生在具体情境中感受到数学在生活实际中的应用,从而激发他们学习数学的兴趣.根据“实际售价=进价+利润”等数量关系列一元一次方程解决与打折销售有关的实际问题.审清题意,找出等量关系是解决问题的关键.另外,商品经济问题的题型很多,让学生触类旁通,达到举一反三,灵活的运用有关的公式解决实际问题,提高学生的数学能力.
