-

人教部编版语文九年级上册写作观点要明确教案
生4:电子游戏还有世界大赛。——世界电子游戏大赛为电子游戏“正名”,倡导国人转变“视电子竞技为洪水猛兽”的心态,而将其作为考验手脑并用能力的一项体育赛事项目。提炼观点:青少年对电子游戏的喜爱可转移到为国争光的竞技项目上。…………2.文题拟定同学们拟定的作文题目可分为两类:一类是能直接看出作者观点的作文题目:如电子游戏危害青少年成长;沉迷电子游戏危害多……另一类是不能直接看出作者观点的作文题目:如电子游戏之我见;我看电子游戏……总的来说,大家直接亮明观点的作文题目都是写电子游戏的危害的。没有直接亮明作者观点的作文题目是既写玩电子游戏的好处也写玩电子游戏的坏处的。其实,很多事物并不是非黑即白的,我们可以把对电子游戏的认识写得更全面、深刻些,让人能从中明白新的道理。

人教部编版语文九年级上册写作议论要言之有据教案
分析是联系论据与论点的桥梁,是丰富文章内容的关键所在。有了分析,事例和论点就能成为有机的统一体;只有通过理性的分析,剖析出事例与论点之间的关系,才能让文章拥有令人信服的逻辑力量。总结:运用论据的时候,对论据进行适当的变化、概括、分析,要有重点、有意识地突出所述事实论据和观点一致的地方,保证所述事实与观点相对应。可参照“分论点+事例+对事例进行分析+结论(照应分论点)”这样的格式来进行论证。【设计意图】以学生小组讨论来得出运用论据的三个方法 ,让学生自己在交流讨论中品味体验。通过“讨论”“交流”等形式实现学生的自主学习,达到培养学生独立思考能力和写作表达能力的目的。五、品读例文,评点“言之有据”1.根据文题,画思维导图课件出示:《论语·为政》中说:“人而无信,不知其可也。”诚信,自古以来就是一种美德。欺诈、造假等不讲诚信的现象历来为人们所深恶痛绝。请以《谈诚信》为题,尝试画一个议论文的思维导图。

人教部编版语文九年级下册写作有创意的表达教案
1.题目具有开放性,可以实写,也可以虚写。展开联想和想象,将自己想到的全列出来,然后再从中确定写作重点。2.从题目看,可以灵活选择文体。比如,可以以写景或抒情为主,也可以进行议论,或者虚构一个故事等,要力求有创意。3.注意表达上的创新,丰富的词语、恰当的修辞等,都可以为文章增色。2.写作指导。(1)审题立意。本题具有开放性,有实虚两重意义。展开联想和想象,可以写实,也可以写它的象征意义,还可以实虚结合。“春天的色彩”既可以指现实中的春天的各种色彩,也可以指象征意义中的“春天”带着“色彩”(以表达某种心情)。如自然的春天、社会的春天、心灵的春天等等。(2)文体选择与表达。在文体方面,可以写成写景或抒情的散文,也可以写议论文,或者写成表达“春天的色彩”这一主题的记叙文。在表达上应有创新,可以用丰富的词汇、变换的句式、新颖的修辞为文章增色。尤其在作文形式上要有所创新。

人教部编版语文八年级上册任务三新闻写作教案
五、布置作业新闻是我们了解社会、了解世界的窗口,每天都有各种各样的新闻发生。虽然新闻写作活动已经结束,但是听新闻、看新闻的活动才刚刚启幕。学了新闻写作的方法,我们再去听新闻、看新闻,就更有针对性,更能了解作者的写作意图。今天的作业比较特殊,是一个长期的作业,即希望同学们能够每天坚持至少听新闻、看新闻十分钟。结束语:同学们,明代思想家顾宪成有名联:“风声雨声读书声声声入耳;家事国事天下事事事关心。”“新闻每天发生,视角各有不同。”网络时代,我们更应该走向更广阔的世界,用一双新闻眼,发现生活中的新闻事件,传播正能量的新闻事实。这是我们的义务,也是我们光荣的责任。【设计意图】写作新闻是提升综合素质的绝佳途径之一,它让我们紧贴时代脉搏,既开阔了视野,又锻炼了思辨能力,还可以学到各种科学新知、流行文化。在学生了解了新闻写作的基本方法后,向他们提出听新闻、看新闻的要求,旨在培养他们关心时事的习惯,为他们的素养提升奠基。

人教部编版语文八年级上册写作表达要得体教案
预设 这篇邀请函格式正确、要素齐全、语言得体。主要表现在:标题直接点明邀请的目的,清晰醒目;格式上有称呼、问候语、祝颂语、落款,符合邀请函的基本格式要求;正文中有邀请的理由,让家长明确被邀请的原因;有活动的时间、地点,以及启动仪式的流程和注意事项,让被邀请者有所了解和准备,更显真诚、有礼。整个邀请函,态度诚恳,简洁明了,表达得体。3.拓展迁移,把握书信体应用文写作格式师:请同学们探讨一下,采用书信格式写作的应用文还有哪些?它们的共同点是什么?预设 感谢信、慰问信、表扬信、申请书(请假条)、倡议书、介绍信、证明信、求职信、应聘信、祝贺信、请柬等。格式一般由六个部分构成,即标题、称呼、问候语、正文、祝颂语、落款。

人教部编版语文八年级下册写作学写读后感教案
师小结:本篇习作开篇概述原作内容,抓住要点,简明扼要。感想的内容,先扣住深沉的父爱,表达自己对傅雷的敬意,然后赞美现实生活中父爱的伟大。思路清晰,情感真挚。【设计意图】以《傅雷家书》读后感写作为例,指导学生如何写读后感。重点指导“点引议联结”的基本结构,让学生写作有章可循。四、尝试写读后感1.写作内容师:同学们已经阅读了《傅雷家书》,请大家回顾内容,自拟题目,按照今天讲的写读后感的方法,先列出写作提纲,再写成作文,不少于600字。2.能力提升用已学的读后感知识,修改自己的作文。并反思所写读后感是否有以下不足:(1)以“引”代“感”。读后感,顾名思义,主要是写“感”,引述是为写“感”服务的,但有些同学往往忘记了这一条,本末倒置,大量抄录或复述原文,结果犯了以“引”代“感”、代“联”的毛病。

人教部编版语文九年级上册写作论证要合理教案
当然,知足常乐者,并不是说这个人要安于现状,没有追求,没有理想,而是要懂得适可而止,懂得取舍,懂得放弃,毕竟人的欲望是无限的。如《我的叔叔于勒》讲述了这样一个故事:年轻时,于勒大肆挥霍,被看成是“祸水”,落得被扫地出门的地步。既至美洲,赚了小钱,两年后又发了大财,成为大家的“福星”。菲利普一家渴盼有钱的于勒归来,二姐也因此找到了未婚夫,一家人都很高兴,出国到哲尔赛岛旅行。他们在船上却见到一个酷似于勒的穷苦的卖牡蛎的人,菲利普先生在船长那里得到了可怕的印证。不但发财的梦想化为乌有,进入上流社会的美梦成为泡影,而且眼下二女儿的婚事也岌岌可危,最后全家不动声色地改乘另一艘海轮回来。菲利普夫妇对于勒的态度完全建立在金钱之上,因此,他们的人生注定不会常乐。被称为“古今隐逸诗人之宗”的陶渊明,在乡野山林中,找到了人生乐趣。大名鼎鼎的诗仙李白,在不得志之时,仍有“天生我材必有用,千金散尽还复来”的达观之句。被林语堂先生称为“无可救药的乐天派”的苏东坡虽一生坎坷,仍对生命和生活充满热爱。所以,知足者,常乐也。人们常说:“人生不如意事十之八九。”那么我们不妨“常想一二”。拥有一颗乐观的心,才是我们成功的关键。

人教部编版语文九年级上册范进中举教案
3.归纳主旨本文通过描写范进参加乡试中了举人一事,运用夸张的手法刻画了他为科举考试喜极而疯的形象,用岳丈在范进中举前后的极其鲜明的肢体动作和言语表情,以及中举后邻居对他的前呼后拥和乡绅赠屋等行为,刻画了一个趋炎附势、热衷仕途、好官名利禄的封建知识分子形象,并且谴责了世态炎凉的可耻的社会风气,对当时的社会及其阴暗面进行了辛辣的讽刺。【设计意图】本板块研读品析了文本中的若干次要人物,引导学生理解次要人物的作用,体会本文侧面烘托的写法,揭示社会环境,点明范进悲剧的必然性,进一步挖掘本文的主旨,使学生理解文本深刻的现实意义。结束语:范进,一个让人啼笑皆非的人物,他卑微可怜,热衷科举,丑态百出。文章塑造这个下层知识分子的典型形象,深刻揭露并辛辣地讽刺了封建科举制度,揭露了封建科举制度的腐朽及其对读书人的腐蚀和毒害。如今,科举制度早已被废除,我们有着公平的人才选拔方式,希望同学们可以珍惜每一个机会,好好努力,实现自己的理想抱负。【板书设计】

人教部编版七年级语文上册如何突出中心教案
我们一家乘车行驶在黄土高原上,眺望远处云朵,尽情享受着清风的洗礼……因为我们要回老家喽!倘若乖乖地欣赏美景,是坐不住的。虽说有起伏不定的高原,波涛汹涌的黄河,不时从石缝里“蹦”出来的水丝帘,一望澄澈的蓝天,悠然飘过的白云……可当这一切的美景同时“刷”在你的眼前,且接连不断地出现时,还是会让你感到几分乏味。因为,这可是八小时的长途跋涉啊!每到这时候,车里的人们就疯狂了起来。虽说只有区区四人,可还是组成了一个超级合唱团。不信你看爸爸已经兴奋起来。只见他清清嗓子,扭动身子,接着便“肆无忌惮”地高声唱起来。妈妈则是一副欲唱又止的样子,最终也只是淡淡地笑了笑。在这一刹那,妈妈神情是最复杂也是最可爱的。是快乐还是骄傲?是幸福还是羞涩?总之,略有些放不开。后来,她也开始有节奏地在车门上敲击,敲出一串美妙又兴奋的声音。好像她所有的快乐都被谱成了一首无拘无束的歌。

人教部编版语文八年级上册中国石拱桥教案
中国的拱桥的历史可追溯到东汉时期,至今已有一千八百多年。中国的拱桥别具一格,造型优美,曲线圆润,形式多样,世界罕见。拱桥按照建筑材料分为石拱桥、砖拱桥和木拱桥,其中较为常见的是石拱桥。拱桥又分为单拱、双拱、多拱,拱的多少根据河面的宽度而定。多拱桥一般正中间的拱较大,两边的拱略小。根据拱的形状,又分五边、半圆、尖拱、坦拱。桥面上铺板,桥边有栏杆。单孔拱桥的拱形呈抛物线的形状,如北京颐和园的汉白玉石桥玉带桥。多孔拱桥适于跨度较大的宽广水面,常见的多为三、五、七孔,以奇数为多,偶数较少。当多孔拱桥某个孔的主拱受荷时,能通过桥墩的变形或拱上结构的作用把荷载由近及远地传递到其他孔主拱上去,这样的拱桥称为连续拱桥,简称“联拱”。如建于唐代元和年间的古桥苏州宝带桥,桥下共有53个孔相连,桥孔之多,结构之精巧,为中外建桥史上所罕见。

精编中学教师教学学习个人心得与感受参考范文
首先,要认真钻研教材,为“预设”打好基础。教材是教学资料的载体,每一位教师都要认真研读、感悟、领会教材,了解教材的基本精神和编写意图,把握教材所带给的数学活动的基本线索,分析教材所渗透的数学思想、方法和学生活动的科学内涵,这样才能体会新教材蕴含的教学理念,备出高质量的教学预案。 其次,要改变备课模式,变“教案”为“学案”。学生是学习的主人,一切知识经验的获得都依靠于学生的自主建构、自我内化。离开了“学”,再精心的“设计”也没有好处,教师要充分思考,预设学生可能出现的状况,并采取相应的对策。即对整个教学过程进行一种有准备、有意识的预设。

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?
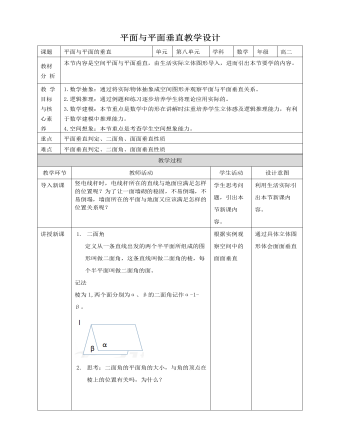
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?

人教A版高中数学必修一三角函数的应用教学设计(2)
本节课是在学习了三角函数图象和性质的前提下来学习三角函数模型的简单应用,进一步突出函数来源于生活应用于生活的思想,让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的创新精神和实践能力.课程目标1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题.2.实际问题抽象为三角函数模型. 数学学科素养1.逻辑抽象:实际问题抽象为三角函数模型问题;2.数据分析:分析、整理、利用信息,从实际问题中抽取基本的数学关系来建立数学模型; 3.数学运算:实际问题求解; 4.数学建模:体验一些具有周期性变化规律的实际问题的数学建模思想,提高学生的建模、分析问题、数形结合、抽象概括等能力.

人教A版高中数学必修一单调性与最大(小)值教学设计(1)
《函数的单调性与最大(小)值}》系人教A版高中数学必修第一册第三章第二节的内容,本节包括函数的单调性的定义与判断及其证明、函数最大(小)值的求法。在初中学习函数时,借助图像的直观性研究了一些函数的增减性,这节内容是初中有关内容的深化、延伸和提高函数的单调性是函数众多性质中的重要性质之一,函数的单调性一节中的知识是前一节内容函数的概念和图像知识的延续,它和后面的函数奇偶性,合称为函数的简单性质,是今后研究指数函数、对数函数、幂函数及其他函数单调性的理论基础;在解决函数值域、定义域、不等式、比较两数大小等具体问需用到函数的单调性;同时在这一节中利用函数图象来研究函数性质的救开结合思想将贯穿于我们整个高中数学教学。

人教A版高中数学必修一函数模型的应用教学设计(2)
本节通过一些函数模型的实例,让学生感受建立函数模型的过程和方法,体会函数在数学和其他学科中的广泛应用,进一步认识到函数是描述客观世界变化规律的基本数学模型,能初步运用函数思想解决一些生活中的简单问题。课程目标1.能利用已知函数模型求解实际问题.2.能自建确定性函数模型解决实际问题.数学学科素养1.数学抽象:建立函数模型,把实际应用问题转化为数学问题;2.逻辑推理:通过数据分析,确定合适的函数模型;3.数学运算:解答数学问题,求得结果;4.数据分析:把数学结果转译成具体问题的结论,做出解答;5.数学建模:借助函数模型,利用函数的思想解决现实生活中的实际问题.重点:利用函数模型解决实际问题;难点:数模型的构造与对数据的处理.

人教A版高中数学必修一充分条件与必要条件教学设计(2)
【例3】本例中“p是q的充分不必要条件”改为“p是q的必要不充分条件”,其他条件不变,试求m的取值范围.【答案】见解析【解析】由x2-8x-20≤0得-2≤x≤10,由x2-2x+1-m2≤0(m>0)得1-m≤x≤1+m(m>0)因为p是q的必要不充分条件,所以q?p,且p?/q.则{x|1-m≤x≤1+m,m>0}?{x|-2≤x≤10}所以m>01-m≥-21+m≤10,解得0<m≤3.即m的取值范围是(0,3].解题技巧:(利用充分、必要、充分必要条件的关系求参数范围)(1)化简p、q两命题,(2)根据p与q的关系(充分、必要、充要条件)转化为集合间的关系,(3)利用集合间的关系建立不等关系,(4)求解参数范围.跟踪训练三3.已知P={x|a-4<x<a+4},Q={x|1<x<3},“x∈P”是“x∈Q”的必要条件,求实数a的取值范围.【答案】见解析【解析】因为“x∈P”是x∈Q的必要条件,所以Q?P.所以a-4≤1a+4≥3解得-1≤a≤5即a的取值范围是[-1,5].五、课堂小结让学生总结本节课所学主要知识及解题技巧

人教A版高中数学必修一充分条件与必要条件教学设计(1)
本课是高中数学第一章第4节,充要条件是中学数学中最重要的数学概念之一, 它主要讨论了命题的条件与结论之间的逻辑关系,目的是为今后的数学学习特别是数学推理的学习打下基础。从学生学习的角度看,与旧教材相比,教学时间的前置,造成学生在学习充要条件这一概念时的知识储备不够丰富,逻辑思维能力的训练不够充分,这也为教师的教学带来一定的困难.“充要条件”这一节介绍了充分条件,必要条件和充要条件三个概念,由于这些概念比较抽象,中学生不易理解,用它们去解决具体问题则更为困难,因此”充要条件”的教学成为中学数学的难点之一,而必要条件的定义又是本节内容的难点.A.正确理解充分不必要条件、必要不充分条件、充要条件的概念;B.会判断命题的充分条件、必要条件、充要条件.C.通过学习,使学生明白对条件的判定应该归结为判断命题的真假.D.在观察和思考中,在解题和证明题中,培养学生思维能力的严密性品质.

人教A版高中数学必修一不同函数增长的差异教学设计(2)
本节课在已学幂函数、指数函数、对数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反应.而本节课重在研究不同函数增长的差异.课程目标1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.数学学科素养1.数学抽象:常见增长函数的定义、图象、性质;2.逻辑推理:三种函数的增长速度比较;3.数学运算:由函数图像求函数解析式;4.数据分析:由图象判断指数函数、对数函数和幂函数;5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结函数性质.重点:比较函数值得大小;难点:几种增长函数模型的应用.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。

人教A版高中数学必修一不同增长函数的差异教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.3节《不同增长函数的差异》 是在学习了指数函数、对数函数和幂函数之后的对函数学习的一次梳理和总结。本节提出函数增长快慢的问题,通过函数图像及三个函数的性质,完成函数增长快慢的认识。既是对三种函数学习的总结,也为后续导数的学习做了铺垫。培养和发展学生数学直观、数学抽象、逻辑推理和数学建模的核心素养。1.了解指数函数、对数函数、幂函数 (一次函数) 的增长差异.2、经过探究对函数的图像观察,理解对数增长、直线上升、指数爆炸。培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;3、在认识函数增长差异的过程中,使学生学会认识事物的特殊性与一般性之间的关系,培养数学应用的意识,探索数学。 a.数学抽象:函数增长快慢的认识;b.逻辑推理:由特殊到一般的推理;









