-

部编人教版四年级下册《琥珀》创新教案
教学重难点:1.使学生了解琥珀形成的过程和形成过程必须具备的条件。2.并从这块琥珀推想出这个故事的过程中发展学生的想象和推理的能力。教学时间:两课时教学过程:第一课时一、谈话引入,揭示课题。1.你们见过琥珀吗?如果见过,谁能给大家介绍一下?2.我们先来欣赏几件美丽珍贵的琥珀艺术品。出示图片。3.最后一幅图为书上的琥珀图片:这是一块怎样的琥珀呢?谁想说一说?作者也向我们介绍了这块琥珀的样子。让我们一起来看看他是怎样描述的。让我们来看课文吧。二、初读课文,整体感知。学生用自己喜欢的方式读课文,提出要求:1.读准字音,读不准的借助工具书或询问老师和同学。2.边读边画出带生字的词,结合语言环境加以理解。3.把课文读得准确、流利。

部编人教版四年级下册《小英雄雨来》创新教案
(二)提问:夜校的学习条件怎样?雨来在夜校里受到什么教育?默读第二段。指导朗读:“我们是中国人,我们爱自己的祖国。”“我们——是——中国人,我们——爱——自己的——祖国。”讨论段意和小标题。(段意:雨来上夜校,受到爱国主义教育。)(小标题:“雨来上夜校。”)(三)学习第三段。默读课文,提问:这段主要说了几层意思?学生默读课文,小组交流,展示如下:(两层意思:第一层从“有一天”至“只从街上传来一两声狗叫”,主要写鬼子开始扫荡了;第二层从“第二天”至这段结束,主要写雨来为掩护交通员李大叔,被鬼子捆绑起来了。)指导朗读第二层。重点朗读:“他抬头一看,是李大叔。”“咦!这是什么时候挖的洞呢?”“把缸搬回原地方。你就快到别的院里去,对谁也不许说。”讨论段意和小标题。段意:(雨来为掩护交通员李大叔,被鬼子捆绑起来了。)(小标题:“雨来掩护李大叔”。)
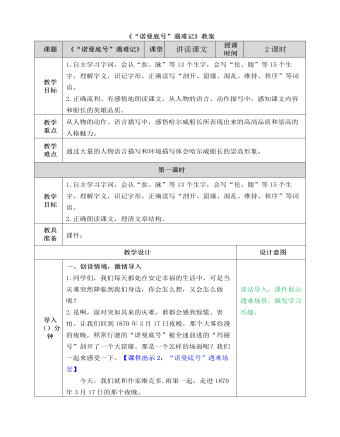
部编人教版四年级下册《 “诺曼底号”遇难记》教案
二、想象品读,体会惊恐万状的场面。1.【课件出示14】教师播放《泰坦尼克号》影片片断录音,学生倾听。2.听了刚才的场景,你感受如何?(好害怕,很恐惧等。)你们听到了什么?又仿佛看到了什么?(生自由回答)面对此情此景,你会首先想到什么呢?要实话实说。(活命、逃命、哭、什么也没想等。)3.师:那么“诺曼底号”上的人们又是怎么表现的呢?请同学们拿起笔,找出相关的段落。【课件出示15】震荡可怕极了。一刹那间,男人、女人、小孩,所有的人都奔到甲板上,人们半裸着身子,奔跑着,尖叫着,哭泣着,惊恐万状,一片混乱。海水哗哗往里灌,汹涌湍急,势不可当。轮机火炉被海浪呛得嘶嘶地直喘粗气。4.指名读文,其他评议。(1)指名学生读,从这段话中你体会到什么?(情况危急、场面混乱等),从哪些词语可以看出来?哪个词语最能体现出人们的表现?(板书:惊恐万状)(读)
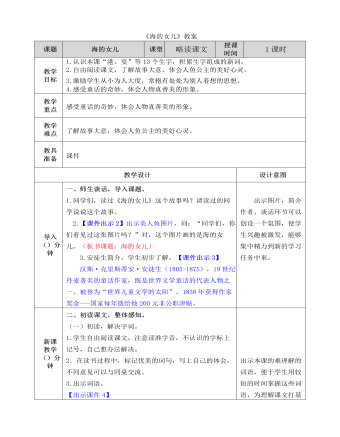
部编人教版四年级下册《海的女儿》教案
《海的女儿》介绍小人鱼亲自参加王子的婚礼,忍受身体和精神的苦痛,一步步变成泡沫,走向死亡的故事。这是一个凄美的爱情故事。成功之处:在教学过程中,以学生为主体,让学生在读通文章之后出示一些重点语句。我在教学中能够放手给学生,让他们在文本中充分品味挖掘语言的魅力内涵。让学生边读边想象,由理解句子表面的意思过渡到感悟作者蕴藏在句子中的情感,小组讨论阶段,学生在充分讨论的过程中对作者的情感就有了一定的感悟,再通过教师的点拨指导,认识上就更深一层次,对今后阅读安徒生的作品帮助很大。不足之处:由于注重了写作方法的学习,对朗读的指导就比较少,在以后的教学中要注意教学时间的合理分配。

部编人教版四年级下册《 短诗三首》教案
一、导入课题,释义诗题1.【出示课件2】《纸船》——寄母亲我从不肯妄弃了一张纸,总是留着——留着,叠成一只一只很小的船儿,从舟上抛下在海里。有的被天风吹卷到舟中的窗里,有的被海浪打湿,沾在船头上。我仍是不灰心的每天的叠着,总希望有一只能流到我要它到的地方去。母亲,倘若你梦中看见一只很小的白船儿,不要惊讶它无端入梦。这是你至爱的女儿含着泪叠的,万水千山求它载着她的爱和悲哀归去。这是冰心先生的一首小诗。让我们一起朗读欣赏。诗歌,让我们用美丽的眼睛看世界。今天就让我们来学习冰心先生的三首短诗。
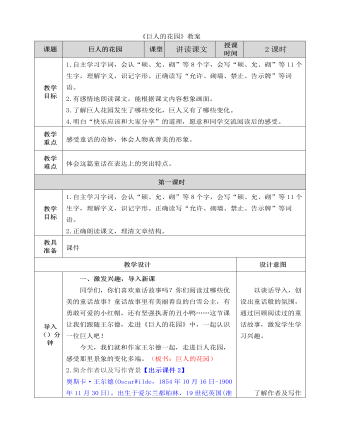
部编人教版四年级下册《 巨人的花园》教案
三、再读感知,理清结构1.学生大声朗读课文,想想:作者是分几个部分介绍巨人花园的?(三个部分)是按照什么顺序将材料串接起来的?(事情发展的顺序)哪些地方给你留下了深刻的印象?2.学生以小组为单位交流读后的收获,教师巡视指导。3.小组推荐一名同学汇报交流的结果,其他同学做补充。4.教师总结。【出示课件6】第一部分(1、2自然段):巨人回来前巨人花园可爱而快乐。第二部分(3-9自然段):巨人回来后驱赶孩童,花园充满凄凉和没有了生机。第三部分(10-15自然段):发现原因后,巨人欢迎孩子,花园又充满快乐。5.概括课文的主要内容。【出示课件7】(本文讲的是巨人回来前巨人花园漂亮而快乐。巨人回来后驱赶孩童,花园充满凄凉,没有了生机。当弄清原因后,巨人欢迎孩子,花园又充满快乐。)

部编人教版四年级下册《古诗词三首》创新教案
二、指导预习。 1.借助汉语拼音读准字音。洗砚池墨痕乾坤2.朗读古诗。3.联系注释,想想每句诗的意思,不理解的词语查字典或者划下来。4.分组交流自己查找到的有关资料。三、检查预习。以读准字音、质疑为重点。四、学习古诗1.了解诗人解诗题。(1)这首诗的作者是谁?(2)《墨梅》作者:元代著名画家王冕。王冕(公元1287——1359)我国元代著名画家。字元章,号煮石山农,诸暨人(今浙江绍兴)。(3)这首诗的题目是什么?(墨梅。这是一首题画诗。墨梅,顾名思义,即为用水墨画的梅花。)(4)从题目上,你知道了什么?还想知道什么?(知道了这首诗写的是水墨画的梅花。想知道这幅梅花图是谁画的?墨梅有什么特点?诗人为什么要写《墨梅》这首诗?要表达自己什么样的感情?)

部编人教版四年级下册《 短诗三首》创新教案
教学目标1.反复朗读优秀诗文,注意在诵读过程中体验情感,展开想象,领悟诗文大意。2.初步了解现代诗的一些特点,体会诗歌的情感。教学过程一、导入新课同学们都读过哪些诗歌呢?你认为读诗歌有什么好处呢?(学生踊跃发言)教师小结:(诗歌能净化人的心灵,升华人的情感。)著名作家冰心的一句话“读书好,多读书,读好书。”就是对名著阅读最好的诠释。

部编人教版四年级下册《记金华的双龙洞》创新教案
教学目标1.认识“浙簇”7个生字,会写“浙罗”15个生字。正确读写“一簇杜鹃突兀森郁臀部漆黑蜿蜒”等词语。2.有感情地朗读课文,能复述“双龙洞”的景象,感受大自然的壮观。3.理解课文记叙的游览顺序,学习有条理叙述的表达方式;体会作者用词造句的准确和朴实。4.感受金华双龙洞自然景观的美,激发学生热爱大自然的情趣。重点难点1.学习按游览顺序记叙的方式和感受孔隙窄小的特点。2.指导学生运用常见的事物,结合自己游览的感觉,把景物特点写具体,使人身临其境的表达方式。教学准备教师搜集有关表现祖国大好山河的风景图、金华双龙洞的文字、图像等资料,做成ppt课件。要求学生提前预习,读课文、认生字、标自然段,制作作者游览过程示意图,现场用展示台予以展示呈现。
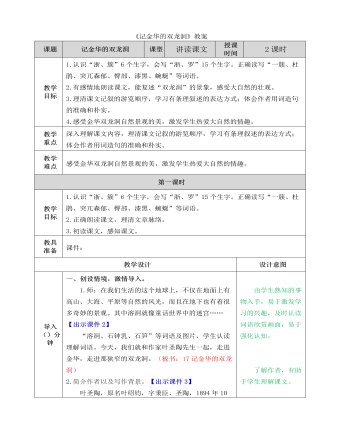
部编人教版四年级下册《记金华的双龙洞》教案
二、“初入溶洞”,感受“美丽”。思考:作者在去双龙洞的途中所见的景物有哪些?【出示课件13】1.粉红色的山,各色的映山红,再加上或浓或淡的新绿,眼前一片明艳。(由具体的景物概括出“明艳”一词,写出金华一带山区明亮艳丽的春色。)2.一路迎着溪流。随着山势,溪流时而宽,时而窄……时时变换调子。引导发现这句话的特点。(如有两对反义词,用拟人手法,写溪水的声音)说说对这句话的理解,体会句子中的因果关系,音韵节奏感,和作者当时的心情等。【出示课件14】预设:一个“迎”字,点明作者是逆溪流而上。(1)“时而……时而……”说明了溪流蜿蜒曲折,因为溪流的宽窄不一,所以才形成流水速度的缓急不同。(2)作者巧妙地运用“宽、窄;缓、急;”两对反义词准确地表达溪流的形和声。由于溪流缓急不一,听到的流水声也就各不相同,犹如在“时时变换调子”。
部编人教版四年级下册《古诗词三首》教案
四、品读诗文,赏析感悟1.品读前两句诗(1)请大家默读前两句,看看都写到了哪几种景物?(雨:什么时候下起了什么样的雨?江:江面上是一番怎样的景象?山:在作者眼里楚山什么样?诗中还暗含着两个人物)【课件出示9】(2)“连”“入”两个动词写“寒雨”表现一种怎样的气氛?(“连”“入”两个动词写“寒雨”的绵绵不断和无声无息,渲染出离别时的暗淡气氛。)“楚山孤”表达作者怎样的情感?(表达诗人离开朋友时的强烈的凄冷孤寂感。)【课件出示10】(板书:凄冷、孤寂感)(3)前两句有一对表示时间的词语:“夜和平明”,王昌龄一共写了两首,这首是天亮时在芙蓉楼送别辛渐时所作,另外一首描绘的是前一天夜里两人在芙蓉楼里饮酒话别时的情景。【课件出示11】(出示第一首诗)师:窗外秋雨绵绵,芙蓉楼内二人相对而坐,饮酒道别,这此情此景,给你一种什么感觉?(凄凉,忧愁)。这种情感凝聚在诗中的哪个字中?(孤)带着这种感觉,再读前两句。师:王昌龄才华横溢,官至县蔚,后来因事被贬谪岭南,在北返长安时在江宁县任职,在江宁数年,又遭人诋毁,再次被贬为龙标县蔚,龙标镇非常偏僻,曾有许多的官员被贬于此地。他一生壮志未酬,与好友分别,心中怎能不孤单、苦闷呢?

北师大初中八年级数学下册三角形的全等和等腰三角形的性质教案
证明:过点A作AF∥DE,交BC于点F.∵AE=AD,∴∠E=∠ADE.∵AF∥DE,∴∠E=∠BAF,∠FAC=∠ADE.∴∠BAF=∠FAC.又∵AB=AC,∴AF⊥BC.∵AF∥DE,∴DE⊥BC.方法总结:利用等腰三角形“三线合一”得出结论时,先必须已知一个条件,这个条件可以是等腰三角形底边上的高,可以是底边上的中线,也可以是顶角的平分线.解题时,一般要用到其中的两条线互相重合.三、板书设计1.全等三角形的判定和性质2.等腰三角形的性质:等边对等角3.三线合一:在等腰三角形的底边上的高、中线、顶角的平分线中,只要知道其中一个条件,就能得出另外的两个结论.本节课由于采用了动手操作以及讨论交流等教学方法,有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

北师大初中八年级数学下册变形后提公因式因式分解教案
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n为正整数).解析:(1)根据已知计算过程直接得出因式分解的方法即可;(2)根据已知分解因式的方法可以得出答案;(3)由(1)中计算发现规律进而得出答案.解:(1)因式分解的方法是提公因式法,共应用了3次;(2)分解因式1+x+x(x+1)+x(x+1)2+…+x(x+1)2015,需应用上述方法2016次,结果是(1+x)2015;(3)1+x+x(x+1)+x(x+1)2+…+x(x+1)n=(1+x)n+1.方法总结:解决此类问题需要认真阅读,理解题意,根据已知得出分解因式的规律是解题关键.三、板书设计1.提公因式分解因式的一般步骤:(1)观察;(2)适当变形;(3)确定公因式;(4)提取公因式.2.提公因式法因式分解的应用本课时是在上一课时的基础上进行的拓展延伸,在教学时要给学生足够主动权和思考空间,突出学生在课堂上的主体地位,引导和鼓励学生自主探究,在培养学生创新能力的同时提高学生的逻辑思维能力.

北师大初中八年级数学下册等腰三角形的判定与反证法教案
方法总结:本题结合三角形内角和定理考查反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况.如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.三、板书设计1.等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(等角对等边).2.反证法(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.解决几何证明题时,应结合图形,联想我们已学过的定义、公理、定理等知识,寻找结论成立所需要的条件.要特别注意的是,不要遗漏题目中的已知条件.解题时学会分析,可以采用执果索因(从结论出发,探寻结论成立所需的条件)的方法.

北师大初中八年级数学下册不等式的基本性质教案
【类型二】 根据不等式的变形确定字母的取值范围如果不等式(a+1)x<a+1可变形为x>1,那么a必须满足________.解析:根据不等式的基本性质可判断a+1为负数,即a+1<0,可得a<-1.方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.三、板书设计1.不等式的基本性质性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变;性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变;性质3:不等式的两边都乘(或除以)同一个负数,不等号方向改变.2.把不等式化成“x>a”或“x<a”的形式“移项”依据:不等式的基本性质1;“将未知数系数化为1”的依据:不等式的基本性质2、3.本节课学习不等式的基本性质,在学习过程中,可与等式的基本性质进行类比,在运用性质进行变形时,要注意不等号的方向是否发生改变;课堂教学时,鼓励学生大胆质疑,通过练习中易出现的错误,引导学生归纳总结,提升学生的自主探究能力.

北师大初中八年级数学下册多边形的内角和与外角和教案
方法总结:解题的关键是由题意列出不等式求出这个少算的内角的取值范围.探究点二:多边形的外角和定理【类型一】 已知各相等外角的度数,求多边形的边数正多边形的一个外角等于36°,则该多边形是正()A.八边形 B.九边形C.十边形 D.十一边形解析:正多边形的边数为360°÷36°=10,则这个多边形是正十边形.故选C.方法总结:如果已知正多边形的一个外角,求边数可直接利用外角和除以这个角即可.【类型二】 多边形内角和与外角和的综合运用一个多边形的内角和与外角和的和为540°,则它是()A.五边形 B.四边形C.三角形 D.不能确定解析:设这个多边形的边数为n,则依题意可得(n-2)×180°+360°=540°,解得n=3,∴这个多边形是三角形.故选C.方法总结:熟练掌握多边形的内角和定理及外角和定理,解题的关键是由已知等量关系列出方程从而解决问题.

北师大初中八年级数学下册分式方程的应用教案
解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,根据题意得14521.1x-1200x=20,解得x=6.经检验,x=6是原方程的解.(2)第一次购买水果1200÷6=200(千克).第二次购买水果200+20=220(千克).第一次赚钱为200×(8-6)=400(元),第二次赚钱为100×(9-6.6)+120×(9×0.5-6.6)=-12(元).所以两次共赚钱400-12=388(元).答:第一次水果的进价为每千克6元;该老板两次卖水果总体上是赚钱了,共赚了388元.方法总结:本题具有一定的综合性,应该把问题分解成购买水果和卖水果两部分分别考虑,掌握这次活动的流程.三、板书设计列分式方程解应用题的一般步骤是:第一步,审清题意;第二步,根据题意设未知数;第三步,根据题目中的数量关系列出式子,并找准等量关系,列出方程;第四步,解方程,并验根,还要看方程的解是否符合题意;最后作答.

北师大初中八年级数学下册分式的基本性质教案
【类型二】 分式的约分约分:(1)-5a5bc325a3bc4;(2)x2-2xyx3-4x2y+4xy2.解析:先找分子、分母的公因式,然后根据分式的基本性质把公因式约去.解:(1)-5a5bc325a3bc4=5a3bc3(-a2)5a3bc3·5c=-a25c;(2)x2-2xyx3-4x2y+4xy2=x(x-2y)x(x-2y)2=1x-2y.方法总结:约分的步骤;(1)找公因式.当分子、分母是多项式时应先分解因式;(2)约去分子、分母的公因式.三、板书设计1.分式的基本性质:分式的分子与分母都乘以(或除以)同一个不为零的整式,分式的值不变.2.符号法则:分式的分子、分母及分式本身,任意改变其中两个符号,分式的值不变;若只改变其中一个符号或三个全变号,则分式的值变成原分式值的相反数.本节课的流程比较顺畅,先探究分式的基本性质,然后顺势探究分式变号法则.在每个活动中,都设计了具有启发性的问题,对各个知识点进行分析、归纳总结、例题示范、方法指导和变式练习.一步一步的来完成既定目标.整个学习过程轻松、愉快、和谐、高效.

北师大初中八年级数学下册分式的有关概念教案
解析:由分式有意义的条件得3x-1≠0,解得x≠13.则分式无意义的条件是x=13,故选C.方法总结:分式无意义的条件是分母等于0.【类型三】 分式值为0的条件若使分式x2-1x+1的值为零,则x的值为()A.-1 B.1或-1C.1 D.1和-1解析:由题意得x2-1=0且x+1≠0,解得x=1,故选C.方法总结:分式的值为零的条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.三、板书设计1.分式的概念:一般地,如果A、B表示两个整式,并且B中含有字母,那么式子AB叫做分式.2.分式AB有无意义的条件:当B≠0时,分式有意义;当B=0时,分式无意义.3.分式AB值为0的条件:当A=0,B≠0时,分式的值为0.本节采取的教学方法是引导学生独立思考、小组合作,完成对分式概念及意义的自主探索.提出问题让学生解决,问题由易到难,层层深入,既复习了旧知识又在类比过程中获得了解决新知识的途径.在这一环节提问应注意循序性,先易后难、由简到繁、层层递进,台阶式的提问使问题解决水到渠成.

北师大初中八年级数学下册分式方程的概念及列分式方程教案
探究点二:列分式方程某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个.设原计划每天生产x个,根据题意可列分式方程为()A.20x+10x+4=15 B.20x-10x+4=15C.20x+10x-4=15 D.20x-10x-4=15解析:设原计划每天生产x个,则实际每天生产(x+4)个,根据题意可得等量关系:(原计划20天生产的零件个数+10个)÷实际每天生产的零件个数=15天,根据等量关系列出方程即可.设原计划每天生产x个,则实际每天生产(x+4)个,根据题意得20x+10x+4=15.故选A.方法总结:此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,找出题目中的等量关系,列出方程.三、板书设计1.分式方程的概念2.列分式方程本课时的教学以学生自主探究为主,通过参与学习的过程,让学生感受知识的形成与应用的价值,增强学习的自觉性,体验类比学习思想的重要性,然后结合生活实际,发现数学知识在生活中的广泛应用,感受数学之美.