-

人教版高中语文必修2《采薇》说课稿
三、疏通课文,体会情感学生朗读一至三节,找出通假字,如“莫”;语助词如“止”“曰”;古今异义词如“启”“居”。以及个别短语如“靡室靡家”“载饥载渴”的结构,结合上《卫风·氓》中出现的相同或类似的结构来理解。检查学生的自学情况,抽查翻译,纠正错误。这三节都以采薇起笔,让学生思考课文呢写了薇菜生长的哪几种形态,有什么作用?学生思考。这个问题不难,但学生回答可能不完整,只点到用于表达士卒思归之情的强烈。老师要补充,用薇菜的生长来反映归期的推移和不定期,思念之情更加沉重。同时在艺术手法上,同《卫风·氓》用“桑叶”来起兴一样,这里也是比兴手法,引出下文。另外,战士们靠野菜来充饥也反映了战士们生活艰苦,兴中有赋。

人教版高中英语必修1Earth quake说课稿
(4)Finally, I will ask the SS what this sentence mean:It is always calm before a storm.Purpose: attract the SS attention and bring them into discussionStep 2: Pre-reading 读前Here, I will do the second question in pre-reading first. I will use the method of brainstorming to ask the SS what will happen before an earthquake; and list the phenomenon on the table. 2. Then I will show the SS the picture of abnormal phenomenon, at the same time, encourage the SS to describe.3、finally, I will summarize these phenomenon4、Do the first question in the pre-reading , Imaging your home begins to shake and you must leave it right away. You have time to take only one thing. What will you take? Why?Purpose: help the SS to get further understanding of the topic and stimulate their interests.Step3: While-reading 阅读(1). Skimming Read the text quickly and catch the meaning of the first and second sentence of each paragraph. Predict the meaning of new words(2).scanning(找读)A. Read the text again. Do the following question.1. When and where were the strange things happening?2. What are they?3. Why did the text say the world seemed to be at an end?4. How was the city destroyed after the quake?5. When did the second quake hit the city? What was the result of that?6. Who came to help Tangshan first? And how?B. Work in pairs to discuss the question.

关爱留守儿童-让爱回家说课稿
在这时,我趁势引导:同学们你们天天和爸爸妈妈生活在一起,吃得饱穿得暖,有人疼有人爱,可很多留守儿童见爸爸妈妈一面都成了一种奢望,他们要自己做饭、自己洗衣,有的还要照顾年迈的爷爷奶奶。同学们,他们多么需要我们伸出友爱的双手啊,我们能为他们做什么呢?队员们很快进行了热烈的谈论:最后达成一致意见,成立中队爱心小组,分别是家务小组、学习辅导小组、娱乐小组,每组8名同学,轮流负责对留守儿童提供力所能及的帮助。分工结束后第五小队的队长,宣读了《关爱留守儿童》倡议书,我们要尽自己的力量让《关爱留守儿童》的活动走出学校、走向社会。短短40分钟的活动结束了,从队员们的笑脸上,可以看出又一颗关爱友善的种子发芽了!

弘扬爱国情,践行价值观说课稿
第三环节:深入研讨——领悟“爱国”各小队展示了活动后,我启发大家讨论四个问题:(1)聆听了《我的中国心》后,你的感想是什么?(2)如何理解社会主义核心价值观中“爱国”的内容?(3)如何发扬爱国主义优良传统,在学校争做“美德好少年”,从而逐步树立起正确的价值观?我鼓励队员们结合自身的情况交流学习体会。第四环节:快乐实践——“爱国”行动第四小队组成了“爱国行动考察团”,他们负责将爱国情感落实在行动上,队员们以快板、三句半的形式,告诉大家爱国无大小,要从点滴做起,让爱国从口号变成行动。通过观看影片《恰同学少年》之“朗读篇”,队员们发出了《爱国倡议书》,真正领悟了“少年雄于地球则国雄于地球”的寓意!最后全体队员共同宣誓,将活动推向了高潮。活动课上四个环节由浅入深,层层递进,充分调动了队员的多种感官参与活动,也达到了本次活动课的目的。

学雷锋精神,创建文明校园说课稿
雷锋精神是什么?这一环节是让学生用简单的词语或句子概括。通过这一活动,让学生概括出雷锋精神的内涵:像无私奉献、乐于助人、为人民服务、勤俭节约、尊老爱幼、勤奋好学、干一行爱一行、言行一致等等都是雷锋精神的体现。我们少年儿童是中国的未来和希望,雷锋精神的发扬和光大,创建文明校园的任务就落在他们的肩上,所以在这里我还设计了为发扬雷锋精神,创建文明校园“我该怎么做”这样的问题,目的就是让他们一起行动起来,学雷锋做好事,并制作了“荣誉”旗,奖励身边的好人好事。活动延伸:这里我设计了一个角色游戏活动——我要义卖献爱心,这个游戏学生们表现得非常积极,他们收集了自己不要的小文具或小玩具,将他们拿到集市上去卖,卖东西获得的钱,捐给王奶奶的孙女,因为王奶奶的孙女生病了,无钱治病。我觉得这个游戏使学生们懂得,一个人只要有爱心,只要愿意去帮助别人,无论什么方式都行,而且在游戏活动中孩子们体会到了帮助别人是一件多么多么快乐的事呀。

人教版新课标小学数学一年级下册多些、少些、多得多、少得多说课稿
在100以内数的范围里,18比50是少得多,但到了万以内数的范围内,可能只是少一些,所以结合具体情境帮助孩子体会是很重要的教学方法。想想做做第1题是小孩在进行拍皮球比赛,让孩子选合适的答案,在小组中说说是怎么想的,孩子在交流中就能体会到12比46少得多,50比46多一些,85比46多得多;想想做做第2题是发生在校园里的一个场景,让孩子自己选合适的答案,说说怎么想的,孩子就能体会到16比38少的多,36比38少一些,40比38多一些;第3题的场景是在商店里,让孩子先讨论、认识“贵多啦”的含义,在进行选择,在选择、辨析时进一步明白贵多啦就是“用的钱多得多”;最后,和孩子进行一些活动,比比身高(孩子和孩子比、老师和孩子比)、比比身边的一些数量大小,让孩子尝试用语言描述的同时体会数量之间的大小关系,感受到数学就在身边。最后由一个游戏结束本节课,让孩子拿一个数同45比一比,自己想两个数让同桌比一比,练习使用多些、少些多的多、少的多描述两个数量之间的大小关系,增强合作能力。

人教版高中生物必修1能量之源—光与光合作用说课稿
1)他们在初中的生物学学习中已具备了一定的关于光合作用的基础知识,也做过“绿叶在光下制造淀粉”这个实验。2)他们具备物质转变和能量变化等相关的化学知识。3)在前面的《降低化学反应活化能的酶》一节的学习中已经学习过简单的对照实验和相关的实验设计原则,使本节课最后的实验设计得以顺利进行。4)他们具有一定的 分析问题的能力,实施问题探究教学是可行的。三、教法和学法根据上述对教材和学生的分析,本节采用以下教法和学法:1)实验法:以实验说明结论。生物学的教学就是实验的教学过程,实验的展示形式有学生分组实验、老师示范实验、动画和图片演示实验等,让实验现象说明问题,而不是直接让学生记住结论。2)问题探究教学发:以问题引发兴趣。整个教学过程要设置好问题,层层展开,层层递进,让新知识与旧知识融为一个整体,让学生在步步上升中攀登到知识的顶峰。3)比较学习法,同时采用多媒体辅助教学,解决光合作用抽象的过程。

在疫情防控最新进展情况通报和部署会上的讲话
严格防控疫情。一是严防疫情反弹外溢。我们对XX镇封控区、管控区及重点暴露场所进行严格管理,连续开展“扫楼敲门”行动,确保相关人员“足不出户”“足不出小区”,防止疫情在社区出现反弹。全市倡导非必要不离XX、非必要不出省。二是严防疫情倒灌。这是为了应对当前全国疫情发展出现的形势变化,我们正在加大力度推进的重要工作。重点是像排查出此次XX疫情首两例病例一样,迅速管控排查出涉疫地区来XX返XX人员,以免新的疫情发生。请广大市民朋友密切留意疫情发展动态,如非必要近期不要前往中高风险地区以及疫情发生地区;

在疫情防控最新进展情况通报和部署会上的讲话发言.docx
一、总体情况:全市疫情总体平稳可控。 12月26日0—24时,我市XX镇新增X例新冠肺炎确诊病例,在集中管理的密切接触者中检测发现。确诊病例XX,XX月XX日作为密切接触者被纳入集中管理,XX月XX日-XX日连续核酸检测阴性,XX月XX日晚核酸检测初筛阳性,XX月XX日复核结果阳性,已转运至定点收治医院隔离治疗,经诊断,为新冠肺炎确诊病例(轻型)。 12月13日至12月26日24时,我市累计报告新冠肺炎确诊病例XX例,均为轻型或普通型,全部都在XX镇,没有发生外溢。由于密切接触者等重点人群尚在医学观察期内,不排除还有续发病例的可能,昨天新增这X例也符合这一预判。目前,全市疫情总体平稳可控。

最新关于全市公共卫生服务体系建设情况的调研报告
(一)疾病预防控制工作成效明显。我市坚持以重大传染病防控、免疫规划、慢性病防治、精神卫生、突发公共卫生事件应急处置为重点,以提高全民健康水平为目标,攻坚克难,锐意进取,开拓创新,全市疾病预防控制和卫生应急工作取得了新成绩。免疫规划工作得到加强,儿童免疫规划一类疫苗免费接种;传染病、重大疾病防控、慢性病防治成效显著。 (二)精神卫生工作实现了新突破。我市启动了重性精神病患者网络管理系统,开展了重性精神病人普查活动,重性精神疾病患者规范化管理水平显著提高。定期举办“心理健康知识大讲堂”、“家长课堂”等免费讲座、开展义诊活动。同时与电视台、电台等新闻媒体合作形式多样的公益性栏目,普及心理、精神卫生健康知识,收到较好效果。

读书节国旗下讲话:让读书成为最美好的生命举止
尊敬的老师、同学们:早上好!今天,我发言的题目是《让读书成为最美好的生命举止》春暖花开的四月,我们将迎来xx三中的第六届读书文化节,每年的这个季节,我们的校园繁花盛开书香飘逸,鲜花装点校道,书香涵养性灵。让我们一同走进翰墨书香的世界,不为分数,不为排名,只因为,阅读,确确实实是一项最美好的生命举止。古人说,书中自有黄金屋,书中自有颜如玉。不可否认,书籍能让我们增长知识和才干,能给我们的未来打下坚实的基础,能给我们带来许许多多可以触摸、可以预期的利益。然而,在这个花香满园的四月,我更愿意提倡同学们去读那种能让人心灵沉静,能促人思考,能给人智慧的书。宋代黄山谷说:一日不读书,尘生其中;两日不读书,言语乏味;三日不读书,面目可憎。就我的理解,这里所说的如果不读就会让人面目可憎的书,不会是那些能产生立竿见影效果的工具书或各类方法大全,也不会是我们许多同学曾经心爱的《知音漫客》或者各类练习册、试题集,而是像曹雪芹的《红楼梦》、罗曼罗兰的《名人传》、培根的《培根论说文集》、摩罗的《悲悯情怀》这样的书

人教版高中政治必修2民主决策:作出最佳的选择教案
教师活动:总结讲评。1、对决策者:有助于决策者充分发扬民主,了解民情,反映民意,集中民智,珍惜民力。有助于决策者把人民的根本利益作为决策的出发点和立足点,增强决策的科学性,避免片面性。2、对公民:有利于促进公民对决策的理解,提高落实决策的自觉性,推动决策的实施。有利于提高公民参与公共事务的热情和信心,锻炼参与决策的能力,增强关心公共生活的政治责任感。教师活动:请同学们看教材第22页课堂探究,讨论如果你来组织这一听证会,应该邀请哪些人参加?如何设置会议程序?学生活动:阅读课本,思考讨论。教师点评:(略)(三)课堂总结、点评本节内容讲述了公民参与民主决策的方式和重要意义,通过学习,要自觉树立决策参与意识,不断提高参与决策的能力。 ★课余作业比较民主决策的不同方式

人教版高中政治必修2民主决策:作出最佳的选择教案
为了进一步增强立法的透明度,提高立法质量,国务院法制办公室将《职工带薪年休假规定(草案)》通过网络征求意见。从政治生活角度分析《职工带薪年休假规定(草案)》向社会征求意见的原因。三、反思总结四、当堂检测1.2008年6月,山西省出台了关于2008年规范教育收费、继续治理教育乱收费工作的实施意见,提出有效的规范治理对策并部署下半年治理教育乱收费工作。如果你想向当地政府反映有关教育乱收费问题,你认为可以采用何种方式和途径①社情民意反映制度②专家咨询制度③社会听证制度④电子邮件、电话、信函A、①③④ B、①②④ C、①④ D、②③2.通过上述方式参与民主决策,有助于决策者A、推动决策的实施,提高落实决策的自觉性B、对决策的理解,锻炼参与决策的能力C、克服官僚主义和不正之风,消除腐败现象D、充分发扬民主,深入了解民情,增强决策的科学性到2007年9月,山东省义务教育阶段学校实行“一费制”收费办法三周年。据此回答3—4题。

人教版高中政治选修3联合国:最具普遍性的国际组织教案
相关链接:联合国推动达成的部军控和裁军条约有:《南极条约》(1959年)、《外层空间条约》(1966年)、《不扩散核武器条约》(1968年)、《海床公约》(1970年)、《禁止生物武器公约》(1971年)、《月球协定》(1976年)、《禁止化学武器公约》(1992年)、《全面禁止核试验条约》(1996年)。2、推动共同发展、促进人类文明——经济方面联合国在经济和社会领域建立了一套庞大、复杂、较为系统的机构即联合国经社系统。经社系统制定指导性原则、政策框架以及行动纲领,规范国际社会各成员的行动方向,推动某些发展问题逐步得到解决。经社系统主持召开重大国际会议,从战略高度协调国际社会的经济和社会发展活动。联合国千年首脑会议制定了千年发展目标,为国际发展合作确立了路线图和时间表。经社系统长期从事开发活动,向有关国家提供发展所需的资金、技术,并帮助制定合适的发展战略和政策,为世界特别是发展中国家的经济社会发展作出了积极贡献。在解决全球环境问题方面,联合国做了大量开创性工作。

人教A版高中数学必修一单调性与最大(小)值教学设计(1)
《函数的单调性与最大(小)值}》系人教A版高中数学必修第一册第三章第二节的内容,本节包括函数的单调性的定义与判断及其证明、函数最大(小)值的求法。在初中学习函数时,借助图像的直观性研究了一些函数的增减性,这节内容是初中有关内容的深化、延伸和提高函数的单调性是函数众多性质中的重要性质之一,函数的单调性一节中的知识是前一节内容函数的概念和图像知识的延续,它和后面的函数奇偶性,合称为函数的简单性质,是今后研究指数函数、对数函数、幂函数及其他函数单调性的理论基础;在解决函数值域、定义域、不等式、比较两数大小等具体问需用到函数的单调性;同时在这一节中利用函数图象来研究函数性质的救开结合思想将贯穿于我们整个高中数学教学。

人教A版高中数学必修一单调性与最大(小)值教学设计(2)
《函数的单调性与最大(小)值》是高中数学新教材第一册第三章第2节的内容。在此之前,学生已学习了函数的概念、定义域、值域及表示法,这为过渡到本节的学习起着铺垫作用。学生在初中已经学习了一次函数、二次函数、反比例函数的图象,在此基础上学生对增减性有一个初步的感性认识,所以本节课是学生数学思想的一次重要提高。函数单调性是函数概念的延续和拓展,又是后续研究指数函数、对数函数等内容的基础,对进一步研究闭区间上的连续函数最大值和最小值的求法和实际应用,对解决各种数学问题有着广泛作用。课程目标1、理解增函数、减函数 的概念及函数单调性的定义;2、会根据单调定义证明函数单调性;3、理解函数的最大(小)值及其几何意义;4、学会运用函数图象理解和研究函数的性质.数学学科素养
北师大初中九年级数学下册商品利润最大问题2教案
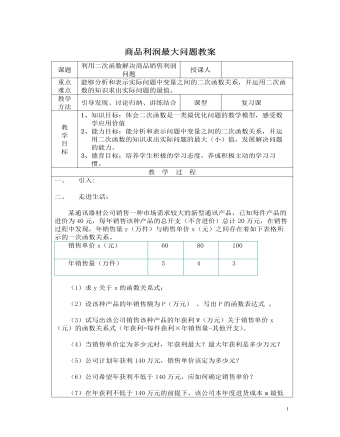
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值


