-

幼儿园环保课说课稿植树造林
二、活动目标: 基于这样一种教育思想,接下来我来说说为本次活动制订的目标。幼儿教育的任何一个目标都应该为幼儿的终生发展作准备,社会教育也不例外。根据幼儿的发展水平、经验、和需要我设计了以下几个目标,分别对幼儿知识、情感、能力方面进行积极的引导。1、知道树木是人类、动物的好朋友,了解绿化的好处,初步产生环保意识。2、迁移生活经验,激发幼儿热爱和亲近大自然的情感。3、通过看看、说说、听听发展幼儿语言表达能力、判断能力。

《劳动最光荣》少先队活动课说课稿
尊敬的各位评委老师:大家好!我叫辛勤,来自邵岗中心小学。今天我说课的主题是:“劳动最光荣”。下面我将从活动背景、活动目标、活动准备、活动过程、活动评价、活动延伸等几个方面作具体的阐述。本次队课的内容选自《少先队活动课指导纲要》养成道德好习惯教育内容。一、说活动背景当前,独生子女是家庭中的主角,在家过着“饭来张口,衣来伸手”的日子,由于从小受到过度娇惯而未形成独立生活的能力,从而表现为对父母的依附性特强。在学校里,这类孩子表现为自立性较差,生活自理能力差,娇气较足。因此,通过《劳动最光荣》活动课的开展,教育学生积极参加自我服务性劳动、力所能及的家务劳动。二、说活动目标本节课要达到两个活动目标:1、知识技能目的立足“班务劳动”、“简单家务”劳动,通过树立榜样、交流窍门、亲自实践等活动,培养学生热爱劳动,劳动光荣的意识,并提高劳动技能。2、情感目的明白劳动能创造财富,劳动能获得快乐,从小养成爱劳动的好习惯。认识到自己的事情应该自己做,父母劳动已经很辛苦,要做到尊敬长辈,热爱长辈。三、说活动准备1、歌曲准备:劳动最光荣。2、幻灯片制作:从古至今,人类离不开劳动。3、搜集日常生活中各行各业的劳动人民给社会做了什么贡献的相关资料。4、课前开展一次班级大扫除。5、各小组准备好本组的劳动展示汇报。6、准备争当“优秀值日生”活动倡议书7、安排好本次活动主持人。8、设计黑板主题“劳动最光荣”。四、说活动过程

《劳动最光荣》少先队活动课说课稿
4、争当班级小主人,为集体出力(建立班集体岗位责任制)五、说活动评价评价激励手段辅导员评价:主要以班级发展主题图中的奖励为主。队员评价:过程评价以星和小奖章记录为主。六、说活动延伸课后各小组建立岗位责任制,全班每个同学都负责一个地方,承担一个责任,由小组长负责和组员讨论如何划分责任区。下周开始执行。最后我想,我们少先队活动课最大的特点就是在活动中体验、在活动中成长。活动全程,队员们的组织能力、观察能力、思考能力、统计能力、团队合作能力、生活能力都得到了锻炼与成长,这就是我们组织少先队活动最大的收获。我们有责任和义务开展好少先队活动课,真正的实现以学生为中心,为学生的长远发展负责,使少先队活动课真正成为育人、育心的课程,更好的为生活服务。以上,就是我对《劳动最光荣》这节少先队活动课的阐述。存在的不足之处还恳请各位评委老师批评指正。谢谢大家!

八年级地理《海陆分布》说课教学
(一)教材的地位和作用《海陆分布》主要介绍世界的海洋与陆地的概况,是学生在学习了《认识地球》等章节的基础上,初步认识世界海陆的分布,是对前面所学习内容的拓展和延伸;同时学好本节有助于学生学习八年级上册的气候、居民及下册的世界分区地理。所以这一节的内容显得十分重要。

八年级人教版一次函数说课稿
1、知识技能目标:掌握一次函数的定义及其解析式的特点、知道一次函数与正比例函数关系、会利用一次函数解决简单的数学问题。2、过程与方法目标: 通过实际问题引出一次函数概念,发展学生探究能力、在教学过程中,让学生学会由具体到抽象,从特殊到一般的数学思想。 3、情感态度与价值观目标: 通过“登山问题”的研究,体会建立函数模型的思想、通过本节课的学习,向学生渗透数学来源于实践生活又反过来作用于实践生活的观念。

人教版三年级上册语文说课稿
二、说教学目标。 1.能用正确的情感来朗读小鸟与大树、树根、门和小女孩四个对话。(知识目标) 2.进一步巩固默读和朗读能力,学会多元交流,多向对话。 (能力目标) 3.体会小鸟与大树间真挚的友情,使学生感悟到真正的友情是建立在诚信的基础上的。

让生命留下痕迹——贝壳说课稿
《贝壳》是人教版七年级上册第四单元中《短文两篇》中的一篇,这一单元以抒发人生感悟为主题,其学习要求是整体把握课文内容,联系自己的生活体验,想想人生的大问题。《贝壳》是一篇托物抒怀的散文,作者席慕蓉作为女性作家,写了一系列极为精致、极蕴内涵的小品,《贝壳》正是其中的佼佼者。

幼儿园安全教案说课稿不乱吃东西
[活动目标]1、通过真实的案例让幼儿懂得随便乱吃东西的危害性。2、引导幼儿乐于探索、交流与分享,激发幼儿的想象力。3、提高自我保护的意识及应对安全事件的能力。[活动准备]真实案例《卡在喉咙里的五角星》;课件《进餐时》、《肚子为什么疼》;情景表演《好吃的鱼》;图片:1、老鼠、苍蝇叮咬过的食物。 2、过期的食物。3、腐烂变质的食物。4、假冒、劣质的食物。5、没洗干净的;每组一小筐(内有图片如:幼儿一边走一边喝水;吃饭时在说笑;吃大量的雪糕;把铅笔放入口中等)

关爱留守儿童-让爱回家说课稿
在这时,我趁势引导:同学们你们天天和爸爸妈妈生活在一起,吃得饱穿得暖,有人疼有人爱,可很多留守儿童见爸爸妈妈一面都成了一种奢望,他们要自己做饭、自己洗衣,有的还要照顾年迈的爷爷奶奶。同学们,他们多么需要我们伸出友爱的双手啊,我们能为他们做什么呢?队员们很快进行了热烈的谈论:最后达成一致意见,成立中队爱心小组,分别是家务小组、学习辅导小组、娱乐小组,每组8名同学,轮流负责对留守儿童提供力所能及的帮助。分工结束后第五小队的队长,宣读了《关爱留守儿童》倡议书,我们要尽自己的力量让《关爱留守儿童》的活动走出学校、走向社会。短短40分钟的活动结束了,从队员们的笑脸上,可以看出又一颗关爱友善的种子发芽了!

弘扬爱国情,践行价值观说课稿
第三环节:深入研讨——领悟“爱国”各小队展示了活动后,我启发大家讨论四个问题:(1)聆听了《我的中国心》后,你的感想是什么?(2)如何理解社会主义核心价值观中“爱国”的内容?(3)如何发扬爱国主义优良传统,在学校争做“美德好少年”,从而逐步树立起正确的价值观?我鼓励队员们结合自身的情况交流学习体会。第四环节:快乐实践——“爱国”行动第四小队组成了“爱国行动考察团”,他们负责将爱国情感落实在行动上,队员们以快板、三句半的形式,告诉大家爱国无大小,要从点滴做起,让爱国从口号变成行动。通过观看影片《恰同学少年》之“朗读篇”,队员们发出了《爱国倡议书》,真正领悟了“少年雄于地球则国雄于地球”的寓意!最后全体队员共同宣誓,将活动推向了高潮。活动课上四个环节由浅入深,层层递进,充分调动了队员的多种感官参与活动,也达到了本次活动课的目的。

养成好习惯践行中国梦说课稿
第七步:全班学生一起倡读承诺书:(课件出示)我们都是小学生,培养习惯最要紧;上课应当专心听,积极开动小脑筋;作业认真仔细做,按时完成交得勤;有了错误要订正,知识才能学得清;人生要有好习惯,我们牢牢记心上。最后请学生把自己要养成的好习惯写在心意卡上,写好后粘贴在教室后面的园地里,互相督促,使得此次活动教育延续课后,直至影响一生.5、活动效果及反思此次活动开展后,学生们增强了对自身的认识,很多学生下决心改掉自身的坏习惯,并逐步采取了实际行动,从身边的小事做起,而且在学生中间还兴起了互相帮助、互相指正、争相进步的热潮。通过此次活动我也切实的体会到养成教育要开展就要落到实处,从实际出发,让学生亲自去感受,去体会,并且要持之以恒的做下去。同时作为老师更应该有一颗敏感热情的心,随时发现学生身上的闪光点与不足,多指正、多指点、多鼓励、多表扬,做到时时处处皆教育,这样才能赢得孩子,做好教育。

追思先烈魂,弘扬爱国情说课稿
环节四深入实践——弘扬爱国情爱国不是一句口号,要将爱国情怀落实到行动中去,队员们在各队队长的组织下,商讨出了落实方案。1、第一小队和第二小队组成了先烈故事演讲团,利用班会十分钟的时间,在三四年级宣讲先烈故事。2、第三小队和第四小队组成了创编小能手,编唱了爱国童谣、爱国拍手歌,告诉大家,爱国无处不在,爱国要从小事做起。3、第五小队和第六小队编写的爱国倡议书,提倡大家让爱国从口号落实到行动。4、全体队员共同宣誓:时刻准备着,为共产主义事业而奋斗,将活动推向了高潮。环节五大队辅导员总结“风雨沧桑,多遭铁蹄践踏,未有沉沦终奋起;荡涤污浊,重聚华夏精魂,披荆斩棘勇向前。”让我们牢记自己是中国人,怀一颗中国心,明确方向,努力奋斗,早日实现自己的梦想。
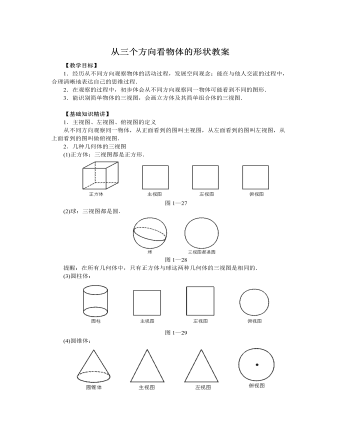
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

北师大初中七年级数学下册三角形的内角和教案
解:∵CE⊥AF,∴∠DEF=90°,∴∠EDF=90°-∠F=90°-40°=50°.由三角形的内角和定理得∠C+∠DBC+∠CDB=∠F+∠DEF+∠EDF,又∵∠CDB=∠EDF,∴30°+∠DBC=40°+90°,∴∠DBC=100°.方法总结:本题主要利用了“直角三角形两锐角互余”的性质和三角形的内角和定理,熟记性质并准确识图是解题的关键.三、板书设计1.三角形的内角和定理:三角形的内角和等于180°.2.三角形内角和定理的证明3.直角三角形的性质:直角三角形两锐角互余.本节课通过一段对话设置疑问,巧设悬念,激发起学生获取知识的求知欲,充分调动学生学习的积极性,使学生由被动接受知识转为主动学习,从而提高学习效率.然后让学生自主探究,在教学过程中充分发挥学生的主动性,让学生提出猜想.在教学中,教师通过必要的提示指明学生思考问题的方向,在学生提出验证三角形内角和的不同方法时,教师注意让学生上台演示自己的操作过程和说明自己的想法,这样有助于学生接受三角形的内角和是180°这一结论

北师大初中数学八年级上册三角形的外角1教案
探究点二:三角形内角和定理的推论2如图,P是△ABC内的一点,求证:∠BPC>∠A.解析:由题意无法直接得出∠BPC>∠A,延长BP交AC于D,就能得到∠BPC>∠PDC,∠PDC>∠A.即可得证.证明:延长BP交AC于D,∵∠BPC是△ABC的外角(外角定义),∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角).同理可证:∠PDC>∠A,∴∠BPC>∠A.方法总结:利用推论2证明角的大小时,两个角应是同一个三角形的内角和外角.若不是,就需借助中间量转化求证.三、板书设计三角形的外角外角:三角形的一边与另一边的延长线所组成的 角,叫做三角形的外角推论1:三角形的一个外角等于和它不相邻的两 个内角的和推论2:三角形的一个外角大于任何一个和它不 相邻的内角利用已经学过的知识来推导出新的定理以及运用新的定理解决相关问题,进一步熟悉和掌握证明的步骤、格式、方法、技巧.进一步培养学生的逻辑思维能力和推理能力,特别是培养有条理的想象和探索能力,从而做到强化基础,激发学习兴趣.

北师大初中数学八年级上册三角形的外角2教案
证法二:(1)延长BD交AC于E(或延长CD交AB于E),如图.则∠BDC是△CDE的一个外角.∴∠BDC>∠DEC.(三角形的一个外角大于任何一个和它不相邻的内角)∵∠DEC是△ABE的一个外角(已作)∴∠DEC>∠A(三角形的一个外角大于任何一个和它不相邻的内角)∴∠BDC>∠A(不等式的性质)(2)延长BD交AC于E,则∠BDC是△DCE的一个外角.∴∠BDC=∠C+∠DEC(三角形的一个外角等于和它不相邻的两个内角的和)∵∠DEC是△ABE的一个外角∴∠DEC=∠A+∠B(三角形的一个外角等于和它不相邻的两个内角的和)∴∠BDC=∠B+∠C+∠BAC(等量代换)活动目的:让学生接触各种类型的几何证明题,提高逻辑推理能力,培养学生的证明思路,特别是不等关系的证明题,因为学生接触较少,因此更需要加强练习.注意事项:学生对于几何图形中的不等关系的证明比较陌生,因此有必要在证明第2小题中,要引导学生找到一个过渡角∠ACB,由∠1>∠ACB,∠ACB>∠2,再由不等关系的传递性得出∠1>∠2。

北师大初中八年级数学下册多边形的内角和与外角和教案
方法总结:解题的关键是由题意列出不等式求出这个少算的内角的取值范围.探究点二:多边形的外角和定理【类型一】 已知各相等外角的度数,求多边形的边数正多边形的一个外角等于36°,则该多边形是正()A.八边形 B.九边形C.十边形 D.十一边形解析:正多边形的边数为360°÷36°=10,则这个多边形是正十边形.故选C.方法总结:如果已知正多边形的一个外角,求边数可直接利用外角和除以这个角即可.【类型二】 多边形内角和与外角和的综合运用一个多边形的内角和与外角和的和为540°,则它是()A.五边形 B.四边形C.三角形 D.不能确定解析:设这个多边形的边数为n,则依题意可得(n-2)×180°+360°=540°,解得n=3,∴这个多边形是三角形.故选C.方法总结:熟练掌握多边形的内角和定理及外角和定理,解题的关键是由已知等量关系列出方程从而解决问题.

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册正方形的判定1教案
∴OE=OF=OG=OH.又∵EG⊥FH,∴四边形EFGH为菱形.∵EO+GO=FO+HO,即EG=HF,∴四边形EFGH为正方形.方法总结:对角线互相垂直平分且相等的四边形是正方形.探究点二:正方形、菱形、矩形与平行四边形之间的关系填空:(1)对角线________________的四边形是矩形;(2)对角线____________的平行四边形是矩形;(3)对角线__________的平行四边形是正方形;(4)对角线________________的矩形是正方形;(5)对角线________________的菱形是正方形.解:(1)相等且互相平分(2)相等(3)垂直且相等(4)垂直(5)相等方法总结:从对角线上分析特殊四边形之间的关系应充分考虑特殊四边形的性质与判别,防止混淆.菱形、矩形、正方形都是平行四边形,且是特殊的平行四边形,特殊之处在于:矩形是有一个角为直角的平行四边形;菱形是有一组邻边相等的平行四边形;而正方形是兼具两者特性的更特殊的平行四边形,它既是矩形,又是菱形.







 QQ登录
QQ登录 微信登录
微信登录