-

北师大初中数学九年级上册比例的性质1教案
若a,b,c都是不等于零的数,且a+bc=b+ca=c+ab=k,求k的值.解:当a+b+c≠0时,由a+bc=b+ca=c+ab=k,得a+b+b+c+c+aa+b+c=k,则k=2(a+b+c)a+b+c=2;当a+b+c=0时,则有a+b=-c.此时k=a+bc=-cc=-1.综上所述,k的值是2或-1.易错提醒:运用等比性质的条件是分母之和不等于0,往往忽视这一隐含条件而出错.本题题目中并没有交代a+b+c≠0,所以应分两种情况讨论,容易出现的错误是忽略讨论a+b+c=0这种情况.三、板书设计比例的性质基本性质:如果ab=cd,那么ad=bc如果ad=bc(a,b,c,d都不等于0),那么ab=cd等比性质:如果ab=cd=…=mn(b+d+…+n≠0), 那么a+c+…+mb+d+…+n=ab经历比例的性质的探索过程,体会类比的思想,提高学生探究、归纳的能力.通过问题情境的创设和解决过程进一步体会数学与生活的紧密联系,体会数学的思维方式,增强学习数学的兴趣.

北师大初中数学九年级上册矩形的性质1教案
解:∵四边形ABCD是矩形,∴AD∥BC,∠A=90°,∴∠2=∠3.又由折叠知△BC′D≌△BCD,∴∠1=∠2.∴∠1=∠3.∴BE=DE.设BE=DE=x,则AE=8-x.∵在Rt△ABE中,AB2+AE2=BE2,∴42+(8-x)2=x2.解得x=5,即DE=5.∴S△BED=12DE·AB=12×5×4=10.方法总结:矩形的折叠问题是常见的问题,本题的易错点是对△BED是等腰三角形认识不足,解题的关键是对折叠后的几何形状要有一个正确的分析.三、板书设计矩形矩形的定义:有一个角是直角的平行四边形 叫做矩形矩形的性质四个角都是直角两组对边分别平行且相等对角线互相平分且相等经历矩形的概念和性质的探索过程,把握平行四边形的演变过程,迁移到矩形的概念与性质上来,明确矩形是特殊的平行四边形.培养学生的推理能力以及自主合作精神,掌握几何思维方法,体会逻辑推理的思维价值.

北师大初中数学九年级上册矩形的判定2教案
2.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形吗?说明理由。答案:四边形ACBE是矩形.因为CD是Rt△ACB斜边上的中线,所以DA=DC=DB,又因为DE=CD,所以DA=DC=DB=DE,所以四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形)。四、课堂检测:1.下列说法正确的是( )A.有一组对角是直角的四边形一定是矩形 B.有一组邻角是直角的四边形一定是矩形C.对角线互相平分的四边形是矩形 D.对角互补的平行四边形是矩形2. 矩形各角平分线围成的四边形是( )A.平行四边形 B.矩形 C.菱形 D.正方形3. 下列判定矩形的说法是否正确(1)有一个角是直角的四边形是矩形 ( )(2)四个角都是直角的四边形是矩形 ( )(3)四个角都相等的四边形是矩形 ( ) (4)对角线相等的四边形是矩形 ( )(5)对角线相等且互相垂直的四边形是矩形 ( )(6)对角线相等且互相平分的四边形是矩形 ( )4. 在四边形ABCD中,AB=DC,AD=BC.请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)

北师大初中数学九年级上册矩形的判定1教案
在△AEF和△DEC中,∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,∴△AEF≌△DEC(AAS),∴AF=DC.∵AF=BD,∴BD=DC;(2)当△ABC满足AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形.∴AB=AC,BD=DC,∴∠ADB=90°.∴四边形AFBD是矩形.方法总结:本题综合考查了矩形和全等三角形的判定方法,明确有一个角是直角的平行四边形是矩形是解本题的关键.三、板书设计矩形的判定对角线相等的平行四边形是矩形三个角是直角的四边形是矩形有一个角是直角的平行四边形是矩形(定义)通过探索与交流,得出矩形的判定定理,使学生亲身经历知识的发生过程,并会运用定理解决相关问题.通过开放式命题,尝试从不同角度寻求解决问题的方法.通过动手实践、合作探索、小组交流,培养学生的逻辑推理能力.

北师大初中数学九年级上册菱形的性质2教案
1. _____________________________________________2. _____________________________________________你会计算菱形的周长吗?三、例题精讲例1.课本3页例1例2.已知:在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=OH.四、课堂检测:1.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,菱形的边长是________cm.2.菱形ABCD的周长为40cm,两条对角线AC:BD=4:3,那么对角线AC=______cm,BD=______cm.3.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 4.已知菱形的面积为30平方厘米,如果一条对角线长为12厘米,则别一条对角线长为________厘米.5.菱形的两条对角线把菱形分成全等的直角三角形的个数是( ).(A)1个 (B)2个 (C)3个 (D)4个6.在菱形ABCD中,CE⊥AB,E为垂足,BC=2,BE=1,求菱形的周长和面积

北师大初中数学九年级上册菱形的判定2教案
方法三:一个同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?请你画一画。通过探究,得到: 的四边形是菱形。证明上述结论:三、例题巩固课本6页例2 四、课堂检测1、下列判别错误的是( )A.对角线互相垂直,平分的四边形是菱形. B、对角线互相垂直的平行四边形是菱形C.有一条对角线平分一组对角的四边形是菱形. D.邻边相等的平行四边形是菱形.2、下列条件中,可以判定一个四边形是菱形的是( )A.两条对角线相等 B.两条对角线互相垂直C.两条对角线相等且垂直 D.两条对角线互相垂直平分3、要判断一个四边形是菱形,可以首先判断它是一个平行四边形,然后再判定这个四边形的一组__________或两条对角线__________.4、已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F求证:四边形AFCE是菱形

北师大初中数学九年级上册菱形的判定1教案
(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC.又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形.又∵EF=BE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为23,∴菱形的面积为4×23=83.方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.三、板书设计菱形的判 定有一组邻边相等的平行四边形是菱形(定义)四边相等的四边形是菱形对角线互相垂直的平行四边形是菱形对角线互相垂直平分的四边形是菱形 经历菱形的证明、猜想的过程,进一步提高学生的推理论证能力,体会证明过程中所运用的归纳概括以及转化等数学方法.在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.

在高质量发展观摩总结会上的表态发言
对项目招引、建设中的难点、堵点、卡点问题,亲自上阵抓协调、抓督查、抓推进,千方百计促落地、促达产、促见效。三是学习借鉴,统筹谋划上再推进。坚持以提升本领为关键,狠抓项目招引建设业务培训和实践锻炼,着力从一切不合时宜的思维定式、固有模式、路径依赖中解放出来,以业务能力提升促进工作成效提升。同时,认真学习其他部门抓项目招引、建设的好经验、好做法,发扬“比学赶超”拼搏精神,在站位上再提升、思路上再调整、方法上再优化、措施上再加力,切实以拼的意识、抢的状态、实的作风推动办公室固定资产投资工作提质增效。我们将认真贯彻落实县委工作部署和此次会议精神,真正把项目建设抓在手里,把责任扛在肩上,全心全意谋划,不遗余力推动,坚决完成固定资产投资任务,向县委交上一份满意答卷。
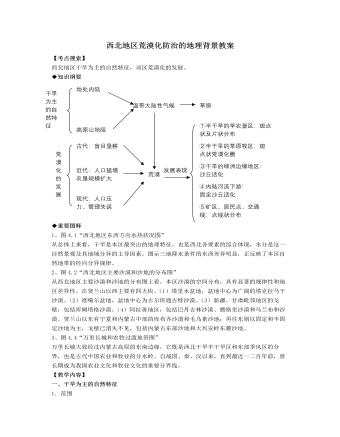
人教版高中地理选修2西北地区荒漠化防治的地理背景教案
【知能训练】一、选择题(第1-4题为单项选择题,第5-6题为双项选择题)1、斑点状土地荒漠化圈主要分布的地方是()A.塔里木河下游绿洲B.呼伦贝尔草原和锡林郭勒草原C.居民点、工矿区及交通线附近D.科尔沁沙地2、近年来,西北地区环境发展的趋势是A.随着人口增加和经济发展,绿洲环境总体趋于好转B.风沙活动增强,盐碱地面积增加C.绿洲经济以农业为主,无环境污染问题D.随着人类对环境影响的加强,绿洲环境向良性方向发展3、我国沙漠沙地所处纬度最高的是()A.科尔沁沙地B.呼伦贝尔沙地C.古尔班通古特沙漠D.乌兰布和沙漠4、我国西北地区干旱为主的自然景观的主要成因是()A.地处北半球亚洲高压的范围之内B.地处东南季风的背风坡C.深居内陆又隔崇山峻岭D.气候干旱、植被稀少、河短水少

人教版高中政治必修4第九课唯物辩证法的实质与核心教案
探究活动8(教材第72页):“结合生活事例,谈谈你在面对复杂事物时是如何分析和解决矛盾的?”这一探究活动是在学生还不了解主次矛盾的原理时,让他们回忆自己在生活中有没有遇到过面对许多矛盾时是如何解决的经历。比如,每天面对很多作业,先做哪门课作业后做哪门作业,你是如何考虑的?在学校面对学习、体育运动和社会工作,你是怎么安排的?在生活中,你遇到这样的情况都是怎样解决的?通过探究活动,使学生弄清主次矛盾的原理,学会用矛盾分析法分析问题。探究活动9(教材第73页):“你在生活中是如何分析具体问题的?”这一探究活动,强调的是“你”在生活中是如何运用分析法分析具体问题的,要紧紧围绕学生这一中心,首先强调具体问题具体分析的方法非常重要,这是马克思主义的一个原则,是马克思主义的活的灵魂。引导学生主动运用这种分析方法分析看待自己,分析看待社会。可以组织学生进行讨论、交流,还可以让学生撰写小论文,写出自己运用这种分析方法分析了哪些具体问题,有哪些感受。

人教版高中政治必修4第九课唯物辩证法的实质和核心精品教案
a矛盾的同一性是矛盾双方相互吸引、相互联结的属性和趋势。它有两方面的含义:一是矛盾双方相互依赖,一方的存在以另一方的存在为前提,双方共处于一个统一体中;同一事物都有对立面和统一面两个方面,一方的存在以另一方为条件,彼此谁都离不开谁(形影想随、一个巴掌拍不响、不是冤家不聚头)。【举例】P67漫画:他敢剪吗?悬挂在山崖上的两个人构成一种动态的平衡。【举例】磁铁(S极和N极);没有上就没有下、没有香就没有臭、没有福就无所谓祸;【举例】父子关系(父亲之所以是父亲,因为有儿子,儿子之所以是儿子,因为有父亲);师生关系;二是矛盾双方相互贯通,即相互渗透、相互包含,在一定条件下可以相互转化。 【相关衔接】P68生物变性现象,雌雄转化现象【举例】生产与消费具有直接统一性

人教版高中政治必修1全面建设小康社会的经济目标教案
3、城镇人口的比重大幅度提高,工农差别、城乡差别、地区差别扩大的趋势逐步扭转请同学们阅读下面材料,结合刚才列举的实例,思考它说明什么问题?2000年我国农村小康总体实现程度在93%左右,城乡收入差距在3:1以上。1999年西部地区小康实现程度为84.18%,中部和东部地区为93.18%、97.86%,人均GDP最高的上海市突破4000美元,最低的贵州省只有300多美元。4、社会保障体系比较健全,社会就业比较充分,家庭财产普遍提高,人民过上更加富足的生活教师活动:请同学们阅读教材102页虚框内材料,思考所提问题学生活动:积极思考,讨论发言。教师总结:说明我国的社会保障体系逐步完善,但是城镇居民保障水平较高,农村社会保障水平还比较低。这与我国的国情是不相适应的,因此,本世纪初20年,要不断健全、完善社会保障体系,集中力量发展经济,降低失业率,提高城乡居民文化教育娱乐等消费比例,让人民的吃穿住行达到更高水平的小康。三、小康社会的建设特点和要求

人教版高中政治必修2民主选举:投出理性的一票教案
教师活动:那种“选举与我无关”,“选谁都可以”的想法,是公民意识不强、主人翁意识不强的表现。那么,怎样才能行使好自己的选举权呢?请同学们根据上面的学习,谈谈自己的想法。学生活动:思考讨论教师点评:2、 如何行使好自己的选举权(1)要不断提高自己参与民主选举的素养,端正参加选举的态度,提高选举能力,选出切实能代表人民利益的人。(2)要增强主人翁责任感和公民参与意识,积极参加选举,认真行使自己的选举权。(3)要不断提高政治参与能力,在理性判断基础上,郑重投出自己的一票。(三)课堂总结、点评本节内容讲述了我国的选举方式以及如何珍惜自己的选举权利的有关知识,懂得我国是人民民主专政的社会主义国家,人民当家作主,应该增强主人翁责任感,自觉珍惜并运用好选举权,以促进我国的民主政治建设,维护人民的根本利益。

人教版高中政治必修4第六课求索真理的历程教案
农业科学的周期是以年为时间单位,一次实验就要等到一次花开、结果。就这样,几个实验误导了袁隆平好几年。这时登在《参考消息》上的一篇不起眼的文章像给迷途中的袁隆平以当头一棒:克里克、沃森和威尔金斯发现DNA螺旋结构,西方的遗传学研究进入分子水平。“我当时还在那里搞什么无性杂交,糟糕得很”。水稻是自花授粉植物,雄蕊雌蕊都在一朵花里面,雌雄同株,没有杂种优势一杂种优势是生物界的普遍现象,小到细菌,大到人,近亲繁殖的结果是种群的退化。但是水稻因为花小,其杂交是当时公认的世界难题,设在马尼拉的世界水稻研究中心就是因为困难重重,差点关闭。袁隆平偏不信这个邪,他突发灵感:专门培养一种特殊的水稻品种——雄花退化的雄性不育系,没有自己的花粉,这样不就可以做到杂种优势了吗?于是,漫长的寻找过程开始了,要找到这样一株雄花退化而且杂交之后产量猛增的“太监”水稻简直是大海捞针。

人教版高中政治必修4第六课求索真理的历程精品教案
二、分析题基于非典型肺炎防治的需要,武汉大学和中国科学院微生物研究所,集中优秀人才和先进的仪器设备,以科学的理论为指导,运用现代的知识与技术手段,对SARS病毒进行深入细致的研究。2003年5月,他们联合研制出抗击SARS病毒侵入细胞的多肽药物。经科学试验证明,它可以阻断SARS病毒侵入人体细胞,具有预防和治疗两种功效。这些药物的发明在非典型肺炎的预防和治疗发挥着重要的作用。上述材料体现了辩证唯物主义认识论的哪些观点?答案提示:体现了实践是认识的来源、实践是认识发展的动力、实践是检验认识的真理性的唯一标准、实践是认识的目的和归宿、认识对实践具有反作用等辩证唯物主义认识论的观点。三、辨析题1、“仁者见仁,智者见智”的说法否定了真理的客观性答案提示:(1)此观点错误。(2)“仁者见仁,智者见智”是说对同一事物不同的人有不同的见解。

人教版高中地理必修3荒漠化的防治—以我国西北地区为例说课稿
(设计意图: 通过这两个问题探究的形式可以了解学生对二、干旱为主的自然特征这一知识点的掌握情况,随堂练习有利于巩固强化学生的条例性知识。)三、荒漠化的成因1、自然因素:干旱、气候异常2、人为因素:(是荒漠化发生、发展的决定因素)自然原因启发学生利用已经学过的知识(干旱为主的自然特征)和给出的PPT资料来进行分析。人为原因以其危害结果用图表和图片的形式展示,使学生认识到人为因素是导致荒漠化最主要的因素。(设计意图:通过分析自然因素提供学生分析一区域环境建设的自然基础条件,而这也是较难的一点,再者,通过分析人为原因,是学生树立区域生态环境保护意识。)四、布置作业:书本课本20—22的活动—— 非洲萨赫勒地区荒漠化的自然、社会经济

人教版高中地理必修3第二章第一节荒漠化的防治教案
1.根据下面的图文资料,说明前苏联垦荒区土壤风蚀的潜在自然背景。并说明人们的生产活动怎样加剧了这个过程。点拨:对图2.16的分析,要知道”垦荒地区”处于亚欧大 陆的中部偏北的地方,虽处于西风带但远离水汽来源,故降水稀少。从其周边的内陆湖“里海”、“咸海”的分布特点,可以推断,这是一个半荒漠向干草原的过渡地带,是一个生态环境比较脆弱的地区,其自然地理状况必定是寒冷、干旱、大风。2.20世纪60年代中期以来,前苏联在总结大规模垦荒经验教训的基础上,采取了一系列综合防护措施。仔细分析这些措施,你认为该地区防治荒漠化(土壤风蚀)的主要方向是什么?点拨:要善于将所列四项保护措施逐条进行分析,而后进行归纳,不难找出它们之间的共同的东西,那就是“抗旱、防风、保水、保土、保肥”。3.根据所学知识,你认为前苏联垦荒区防治荒漠化的对策与措施可以被我国的哪些地区所借鉴。

北师大版小学数学五年级上册《3的倍数的特征》说课稿
一个数各个位上的数字之和如果是3的倍数,那么,这个数一定是3的倍数。否则,这个数就不是3的倍数。4、检验结论。(1)我们从100以内的数中发现了规律,得出了3的倍数的特征,如果是三位数甚至更大的数,3的倍数的特征是否也相同呢?(2)利用100以内数表来验证。(3)延伸到三位数或更大的数。如:573、753、999、1236、2244、7863……(4)学生自己写数并验证,然后小组交流,观察得出的结论是否相同。在本环节,我用充足的时间让小组代表上讲台展示成果,说出各自的思考过程,对学生的回答我给予充分的肯定和表扬,引导学生验证自己的发现是否正确,最后达成共识:一个数的各位上的数的和是3的倍数,这个数就3的倍数(板书)。这样便巧妙地突出本课的重点,突破了本课的难点。

北师大初中数学九年级上册一元二次方程的根与系数的关系1教案
方程有两个不相等的实数根.综上所述,m=3.易错提醒:本题由根与系数的关系求出字母m的值,但一定要代入判别式验算,字母m的取值必须使判别式大于0,这一点很容易被忽略.三、板书设计一元二次方程的根与系数的关系关系:如果方程ax2+bx+c=0(a≠0) 有两个实数根x1,x2,那么x1+x2 =-ba,x1x2=ca应用利用根与系数的关系求代数式的值已知方程一根,利用根与系数的关系求方程的另一根判别式及根与系数的关系的综合应用让学生经历探索,尝试发现韦达定理,感受不完全的归纳验证以及演绎证明.通过观察、实践、讨论等活动,经历发现问题、发现关系的过程,养成独立思考的习惯,培养学生观察、分析和综合判断的能力,激发学生发现规律的积极性,激励学生勇于探索的精神.通过交流互动,逐步养成合作的意识及严谨的治学精神.

北师大初中数学九年级上册一元二次方程的根与系数的关系2教案
3、一般地,对于关于 方程 为已知常数, ,试用求根公式求出它的两个解x1、x2,算一算x1+x2、x1?x2的值,你能得出什么结果?与上面发现的现象是否一致。【知识应用】 1、(1)不解方程,求方程两根的和两根的积:① ② (2)已知方程 的一个根是2,求它的另一个根及 的值。(3)不解方程,求一 元二次方程 两个根的①平方和;②倒数和。(4)求一元二次方程,使它的两个根是 。【归纳小结】【作业】1、已知方程 的一个根是1,求它的另一个根及 的值。2、设 是方程 的两个根,不解方程,求下列各式的值。① ;② 3、求一个一元次方程,使它的两 个根分别为:① ;② 4、下列方程两根的和与两根的积各是多少 ?① ; ② ; ③ ; ④ ;
