-

《原始狩猎图》教案
教学过程:1、情景创设、音乐表演:乐曲《原始狩猎图》展示了一幅远古时期人们在夜幕中狩猎的画面,刻画了先民们从发现猎物时的激动到捕获猎物后的狂喜场面。这些场面对我们的学生来说是陌生的,如果让学生去感受一些陌生的东西,容易产生隔膜,难以调动学习的主动性。针对这样存在的问题,我为学生创设了情景,然后请一些同学在音乐情景下表演。以音乐《原始狩猎图》的“引子”作为导入,随着我的描绘补充演绎出完整的远古人狩猎的场景,使学生感受出音乐的古朴音调、神秘和粗犷的音乐风格及独特的音响色彩。2、分段欣赏:乐曲《原始狩猎图》是一首情节性、故事性很强的作品。让同学们再认真聆听过作品后分段赏析每个部分的音乐带给我们的不同的感受。让同学们说出自己所听到的每个不同的部分所讲述的内容。3、学习演奏:让同学们选出大家都比较感兴趣的段子,在老师的带领下大家一起来学习用骨笛演奏。并让大家分析骨笛的声音与一般竹笛声音的不同之处。4、创编动作、情景复现:根据钱兆熹的骨哨与乐队《原始狩猎图》之“庆功”和“尾声”,以及壁画、岩刻上的舞蹈动作,请学生手拉手,老师带头,随着音乐,编创造型和动作,跳起欢庆狩猎成功的舞蹈。5、小结,结束本课。

《原始狩猎图》教案
教学过程:(一)创设情景、借景导入。以音乐《原始狩猎图》的“引子”作为导入,随着我的描绘补充演绎出完整的远古人狩猎的场景,使学生感受出音乐的古朴音调、神秘和粗犷的音乐风格及独特的音响色彩。(二)探访远古、艺术再现。1、欣赏关于远古时期的壁画、岩刻。内容包括:动物、放牧、舞蹈、战争等。绘画手法:壁画一般是勾线涂色;岩刻一般是敲凿和磨刻。绘画工具:壁画用的是苔藓类植物、兽毛,颜料是动物的脂肪和血调和的天然矿物;岩刻用的是石头。2、讨论:远古人为什么会将这些动物刻画在岩石或洞穴中呢?远古人或是为了了解生活中的动物,或是为了记录某一次打猎的过程,或是为了记录每次打猎的成绩,或是为了祈求明天能打到更多的猎物等等原因。3、了解古代的一些乐器(埙、骨哨、骨笛等,链接音频)。(三)欣赏音乐、探究讨论。1、聆听音乐骨哨与乐队《原始狩猎图》之“狩猎”。(1)想想音乐所表现的画面情景。(2)说说乐器“骨哨”和“埙”的音色特点。(3)谈谈听完音乐后的感受。

《原始狩猎图》教案
教学过程:(一)认真聆听这首音乐,配合老师展示的一些关于原始人类狩猎的图片逐渐进入情境。(二)完整欣赏、借景抒情。1、聆听钱兆熹的骨哨与乐队《原始狩猎图》之“庆功”和“尾声”,让学生根据音乐,描绘出想象中的狩猎后古人们跳舞欢庆和散去的场景。2、欣赏花山岩画、舞蹈纹彩陶盆。3、模仿古人的舞蹈动作,简单的举手、手拉手等动作。4、分析乐曲的结构:引子——狩猎——庆功——尾声。5、探究讨论、情感抒发。(1)音乐与情景内容是怎样结合在一起的?(2)古代人为什么要聚在一起狩猎?对我们有什么启发?(3)体会艺术与生活的关系、集体主义精神。(三)艺术拓展、电影与古乐。1、电影《菊豆》与陶埙。2、编钟、编磬。让学生观看影片中配有乐器音乐的片段,在声音与画面,音乐与内容的交互中熟悉古代乐器的声音、音乐的内涵及古乐的魅力。(四)师生总结、情感升华。乐曲采用简洁朴素的音乐语言,充分发挥了骨哨独特的音色和淳朴的艺术魅力,展示了一幅远古时期人们在夜幕中狩猎的画面,把先民们从发现猎物时的激动心情到捕获猎物后的狂喜场面刻画得栩栩如生。谁说国乐不如洋?中华五千年灿烂文明,中国古典音乐有着极高的艺术境界。热爱国乐吧!因为它是我们的母体文化之一!

《拯救地球》教案
教学过程:一、导入同学们,你们知道“迈克尔杰克逊”吗?迈克尔·杰克逊(Michael Jackson),1958年08月29日在美国印第安纳州加里市出生,美国歌手、词曲创作人、舞蹈家、表演家、慈善家、音乐家、人道主义者、和平主义者、慈善机构创办人。1982年12月,杰克逊音乐生涯最畅销的专辑《Thriller》发行。1987年9月,杰克逊展开个人首次全球巡演。通过舞台和视频的表演,杰克逊普及了一些像机械舞和太空步等舞蹈技术。杰克逊一生中两次入选的摇滚名人堂,获得了13个格莱美奖和26个全美音乐奖。在他单飞生涯中,他拥有13支美国冠军单曲。2000年吉尼斯世界纪录大全里认证他资助过39个慈善机构。二、新课教学1、播放《拯救地球》初次聆听,谈谈你的感受。2、简介歌曲来源及故事背景1991年创作,Heal The World 是为了配合迈克尔自己的同名慈善组织所作,Heal the world是一首呼唤世界和平的歌曲,相当优秀,歌词倡导人们保护和珍惜我们的环境,让战争远离,世界和平,我们的心中都有一个地方,那就是爱,让我们营造一个没有战争、没有荒地,生机勃勃,到处充满了温暖和关怀的世界,让孩子们可以自由的欢笑,让世界充满爱。

《月牙儿五更》教案
教学目标:欣赏《月牙儿五更》器乐和声乐曲各有什么特点?教学重、难点1、重点:欣赏《月牙儿五更》,感受民歌改编的器乐作品。2、难点:比较《月牙儿五更》器乐和声乐表现形式的特点。教学过程:一、导入1、根据课题《神州音韵》,导入我国幅员辽阔,拥有多样的地形地貌和复杂的地理环境。同时,我国还是个拥有五十六个民族的大家庭,人们在生活中创造了丰富多彩的民族民间音乐。本节课,我们所学习的音乐都是我们国家的民族音乐。2、同学们对我国的民歌有多少了解?同学讨论,老师补充。二、欣赏《月牙儿五更》1、本节所欣赏的是板胡独奏《月牙儿五更》,所以先了解乐器板胡,看图片,了解板胡的构造。2、聆听与思考:很多优秀的民歌被作曲家改编成了器乐曲,试比较《月牙儿五更》器乐和声乐表现形式各有什么特点?三、结束希望同学们在以后的生活中多了解、喜爱我们的民族音乐,感受民族音乐的独特魅力。

《月牙儿五更》教案
教学过程一、导入教师:同学们,今天老师要带领大家到东北地区,去欣赏东北民歌。二、新课教学1、教师:关东支脉音乐的体裁形式和风格特点与齐鲁燕赵支脉有许多相同之处,但又形成了自身的特点。接下来我们通过几首有代表性的作品来找出关东支脉音乐的风格特点。2、教师播放《月牙儿五更》,请学生思考这首歌曲属于音乐民歌中的哪一种。学生回答回忆上节的知识。3、教师:大家能不能说出这首《月牙儿五更》是由什么乐器演奏的呢?学生回答。教师:板胡是我国弓弦乐器。音箱不是蒙以皮革,而是盖上薄的木板或椰壳,形似碗状,琴干琴弓比二胡粗;音色高亢嘹亮。下面我们来听两段音乐,请大家分辨一下是二胡的音色还是板胡的音色。学生回答。4、教师:下面,老师给大家介绍一位男高音歌唱家郭颂,郭颂演唱了很多优秀的民歌,我们来欣赏一首由他演唱的《月牙儿五更》。学生欣赏乐曲教师:由此我们可以看出很多器乐作品都源于优秀的民歌,民歌是我们源于创作的源泉。让学生了解民歌是音乐创作的源泉。三、课堂小结教师:同学们,今天这节课我们欣赏了关东支脉地区的音乐,我们了解了它的风格特点,也了解了很多的音乐创作都来源于民歌。希望在课下,同学们能够多去了解欣赏民歌,让民歌的灿烂文化一直发扬光大。

大班美术教案:家
2、发展幼儿的想象力和初步的合作能力。二、活动重点:根据纸盒外形想象装饰。三、活动难点:用装饰、拼搭的形式表现出自己的家。

大班美术教案
一、导入。1. 组织游戏《猜猜我是谁》,请幼儿闭上眼睛用手触摸被猜幼儿的脸,然后说出被猜幼儿的姓名,并引导幼儿说说你是怎么发现的。(如,他的脸比较长、他的眼睛很大、她的嘴巴很小等。)2. 请幼儿说说你喜欢的人是谁,他长的什么样?引导幼儿说出人物的典型特征。3. 幼儿仔细观察自己喜欢的人的脸,再与画册中的人物相比较,看与哪一张脸相同。4. 请幼儿为自己喜欢的人画一张像,引导幼儿把人物的典型特征表现出来。二、作画。1. 幼儿开始作画,教师为作画有困难的幼儿做指导。2. 出示范画,请幼儿欣赏并说出范画中人物的典型特征。引导幼儿抓住典型特3. 征大胆表现。

北师大初中数学八年级上册二次根式的混合运算2教案
本节课开始时,首先由一个要在一块长方形木板上截出两块面积不等的正方形,引导学生得出两个二次根式求和的运算。从而提出问题:如何进行二次根式的加减运算?这样通过问题指向本课研究的重点,激发学生的学习兴趣和强烈的求知欲望。本节课是二次根式加减法,目的是探索二次根式加减法运算法则,在设计本课时教案时,着重从以下几点考虑:1.先通过对实际问题的解决来引入二次根式的加减运算,再由学生自主讨论并总结二次根式的加减运算法则。2.四人小组探索、发现、解决问题,培养学生用数学方法解决实际问题的能力。3.对法则的教学与整式的加减比较学习。在理解、掌握和运用二次根式的加减法运算法则的学习过程中,渗透了分析、概括、类比等数学思想方法,提高学生的思维品质和兴趣。

北师大初中数学八年级上册二次根式的运算2教案
1.关于二次根式的概念,要注意以下几点:(1)从形式上看,二次根式是以根号“ ”表示的代数式,这里的开方运算是最后一步运算。如 , 等不是二次根式,而是含有二次根式的代数式或二次根式的运算;(2)当一个二次根式前面乘有一个有理数或有理式(整式或分式)时,虽然最后运算不是开方而是乘法,但为了方便起见,我们把它看作一个整体仍叫做二次根式,而前面与其相乘的有理数或有理式就叫做二次根式的系数;(3)二次根式的被开方数,可以是某个确定的非负实数,也可以是某个代数式表示的数,但其中所含字母的取值必须使得该代数式的值为非负实数;(4)像“ , ”等虽然可以进行开方运算,但它们仍属于二次根式。2.二次根式的主要性质(1) ; (2) ; (3) ;(4)积的算术平方根的性质: ;(5)商的算术平方根的性质: ;
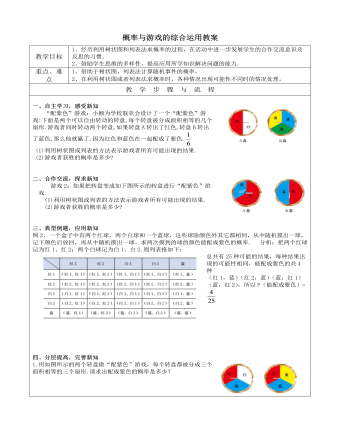
北师大初中数学九年级上册概率与游戏的综合运用2教案
三、典型例题,应用新知例2、一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率. 分析:把两个红球记为红1、红2;两个白球记为白1、白2.则列表格如下:总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),所以P(能配成紫色)= 四、分层提高,完善新知1.用如图所示的两个转盘做“配紫色”游戏,每个转盘都被分成三个面积相等的三个扇形.请求出配成紫色的概率是多少?2.设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为 五、课堂小结,回顾新知1. 利用树状图和列表法求概率时应注意什么?2. 你还有哪些收获和疑惑?

北师大初中七年级数学上册截一个几何体教案1
解析:当截面与轴截面平行时,得到的截面的形状为长方形;当截面与轴截面斜交时,得到的截面的形状是椭圆;当截面与轴截面垂直时,得到的截面的形状是圆,所以截面的形状不可能是三角形.故选A.方法总结:用平面去截圆柱时,常见的截面有圆、椭圆、长方形、类似于梯形、类似于拱形等.探究点三:截圆锥问题一竖直平面经过圆锥的顶点截圆锥,所得到的截面形状与下图中相同的是()解析:经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线.如图,由图可知得到的截面是一个等腰三角形.故选B.方法总结:用平面去截圆锥,截面的形状可能是三角形、圆、椭圆等.三、板书设计教学过程中,强调学生自主探索和合作交流,经历操作、抽象、归纳、积累等思维过程,从中获得数学知识与技能,发展空间观念和动手操作能力,同时升华学生的情感态度和价值观.

北师大初中七年级数学上册有理数的乘法法则教案1
解:由题意得a+b=0,cd=1,|m|=6,m=±6;∴(1)当m=6时,原式=06-1+6=5;(2)当m=-6时,原式=0-6-1+6=5.故a+bm-cd+|m|的值为5.方法总结:解答此题的关键是先根据题意得出a+b=0,cd=1及m=±6,再代入所求代数式进行计算.探究点三:有理数乘法的应用性问题小红家春天粉刷房间,雇用了5个工人,干了3天完成;用了某种涂料150升,费用为4800元,粉刷的面积是150m2.最后结算工钱时,有以下几种方案:方案一:按工算,每个工100元;(1个工人干1天是一个工);方案二:按涂料费用算,涂料费用的30%作为工钱;方案三:按粉刷面积算,每平方米付工钱12元.请你帮小红家出主意,选择哪种方案付钱最合算(最省)?解析:根据有理数的乘法的意义列式计算.解:第一种方案的工钱为100×3×5=1500(元);第二种方案的工钱为4800×30%=1440(元);第三种方案的工钱为150×12=1800(元).答:选择方案二付钱最合算(最省).方法总结:解此题的关键是根据题意列出算式,计算出结果,比较得出最省的付钱方案.

北师大初中七年级数学上册有理数的除法教案1
解析:∵ab>0,根据“两数相除,同号得正”可知,a、b同号,又∵a+b<0,∴可以判断a、b均为负数.故选D.方法总结:此题考查了有理数乘法和加法法则,将二者综合考查是考试中常见的题型,此题的侧重点在于考查学生的逻辑推理能力.让学生深刻理解除法是乘法的逆运算,对学好本节内容有比较好的作用.教学设计可以采用课本的引例作为探究除法法则的过程.让学生自己探索并总结除法法则,同时也让学生对比乘法法则和除法法则,加深印象.并讲清楚除法的两种运算方法:(1)在除式的项和数字不复杂的情况下直接运用除法法则求解.(2)在多个有理数进行除法运算,或者是乘、除混合运算时应该把除法转化为乘法,然后统一用乘法的运算律解决问题.

北师大初中数学八年级上册认识勾股定理1教案
方法总结:题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.探究点二:利用勾股定理求面积如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中△ABE的面积为________,阴影部分的面积为________.解析:因为AE=BE,所以S△ABE=12AE·BE=12AE2.又因为AE2+BE2=AB2,所以2AE2=AB2,所以S△ABE=14AB2=14×32=94;同理可得S△AHC+S△BCF=14AC2+14BC2.又因为AC2+BC2=AB2,所以阴影部分的面积为14AB2+14AB2=12AB2=12×32=92.故填94、92.方法总结:求解与直角三角形三边有关的图形面积时,要结合图形想办法把图形的面积与直角三角形三边的平方联系起来,再利用勾股定理找到图形面积之间的等量关系.

北师大初中数学九年级上册相似三角形判定定理的证明1教案
当Δ=l2-4mn<0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个点P;当Δ=l2-4mn=0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个点P;当Δ=l2-4mn>0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个点P.方法总结:由于相似情况不明确,因此要分两种情况讨论,注意要找准对应边.三、板书设计相似三角形判定定理的证明判定定理1判定定理2判定定理3本课主要是证明相似三角形判定定理,以学生的自主探究为主,鼓励学生独立思考,多角度分析解决问题,总结常见的辅助线添加方法,使学生的推理能力和几何思维都获得提高,培养学生的探索精神和合作意识.
北师大初中七年级数学上册有理数的加法法则教案1
方法总结:股票每天的涨跌都是在前一天的基础上进行的,不要理解为每天都是在67元的基础上涨跌.另外熟记运算法则并根据题意准确列出算式也是解题的关键.三、板书设计加法法则(1)同号两数相加,取与加数相同的符号,把绝对 值相加.(2)异号两数相加,取绝对值较大加数的符号,并 用较大的绝对值减去较小的绝对值.(3)互为相反数的两数相加得0.(4)一个数同0相加,仍得这个数.本课时利用情境教学、解决问题等方法进行教学,使学生在情境中提出问题,并寻找解决问题的途径,因此不知不觉地进入学习氛围,把学生从被动学习变为主动想学.在本节教学中,要坚持以学生为主体,教师为主导,充分调动学生的兴趣和积极性,使他们最大限度地参与到课堂的活动中.

北师大初中数学八年级上册验证勾股定理1教案
探究点二:勾股定理的简单运用如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.解析:运用“两点之间线段最短”先确定出P点在A1B1上的位置,再利用勾股定理求出AP+BP的长.解:作点B关于MN的对称点B′,连接AB′,交A1B1于P点,连BP.则AP+BP=AP+PB′=AB′,易知P点即为到点A,B距离之和最短的点.过点A作AE⊥BB′于点E,则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).由勾股定理,得B′A2=AE2+B′E2=82+62,∴AB′=10(km).即AP+BP=AB′=10km,故出口P到A,B两村庄的最短距离和是10km.方法总结:解这类题的关键在于运用几何知识正确找到符合条件的P点的位置,会构造Rt△AB′E.三、板书设计勾股定理验证拼图法面积法简单应用通过拼图验证勾股定理并体会其中数形结合的思想;应用勾股定理解决一些实际问题,学会勾股定理的应用并逐步培养学生应用数学解决实际问题的能力,为后面的学习打下基础.

北师大初中数学八年级上册轴对称与坐标变化1教案
解析:从各点的位置可以发现A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),A6(2,2),A7(-2,2),A8(-2,-2),A9(3,-2),A10(3,3),A11(-3,3),A12(-3,-3),….仔细观察每四个点的横、纵坐标,发现存在着一定规律性.因为2015=503×4+3,所以点A2015在第二象限,纵坐标和横坐标互为相反数,所以A2015的坐标为(-504,504).故填(-504,504).方法总结:解决此类题常用的方法是通过对几种特殊情况的研究,归纳总结出一般规律,再根据一般规律探究特殊情况.三、板书设计轴对称与坐标变化关于坐标轴对称作图——轴对称变换通过本课时的学习,学生经历图形坐标变化与图形的轴对称之间的关系的探索过程,掌握空间与图形的基础知识和基本作图技能,丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维,激发数学学习的好奇心与求知欲.教学过程中学生能积极参与数学学习活动,积极交流合作,体验数学活动的乐趣.
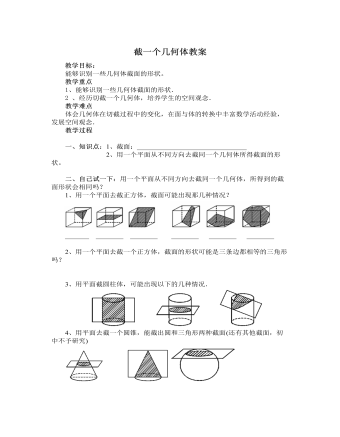
北师大初中七年级数学上册截一个几何体教案2
[例3]、用一个平面去截一个几何体,截面形状有圆、三角形,那么这个几何体可能是_________。四、巩固强化:1、一个正方体的截面不可能是( )A、三角形 B、梯形 C、五边形 D、七边形2、用一个平面去截五棱柱,边数最多的截面是_______形.3*、用一个平面去截几何体,若截面是三角形,这个几何体可能是__________________________________________________.4*、用一个平面截一个几何体,如果截面是圆,你能想象出原来的几何体可能是什么吗?如虹截面是三角形呢?5*、如果用一个平面截一个正方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?6*、几何体中的圆台、棱锥都是课外介绍的,所以我们就在这个栏目里继续为大家介绍这两种几何体的截面.(1)圆台用平面截圆台,截面形状会有_____和_______这两种较特殊图形,截法如下: