-
《黄土高坡》教案
(一)学生随《乡下的阳光》进教室,师生问好。(二)聆听《黄土高坡》、《洞庭鱼米乡》。1、引入:我们生活在江南,你有没有在电影或电视中看到我国黄土高原?出示地图,找一找黄土高坡的位置。(在我国西北)2、在《黄土高坡》背景音乐下,展示CAL课件中的黄土高原的风土人情的图片:(1)漫漫黄土,低矮的窑洞。(2)沙尘漫漫飞舞。(3)人们在劳动。3、师:是啊,虽然黄土高原自然条件恶劣,但世代居住在这里的人们依然热爱他们的家乡,热爱他们的这一片土地,让我们听听他们的歌《黄土高坡》。设问:这首歌曲给你什么感受?4、刚才我们到了黄土高坡,现在我们一起去有“鱼米之乡”的洞庭湖吧。一起在地图上找一找洞庭湖的位置。(在我国中南)(课件播放洞庭湖区秀丽风景和人们张网捕鱼的图片。(同时播放《洞庭鱼米乡》背景音乐。)

人教版高中地理必修3地理信息技术在区域地理环境研究中的应用说课稿
通过列表对比法、归纳法、、多媒体辅助法等教学方法,突破理论性强、不宜理解的“3S”原理与区别的知识难点。学生更是学会运用图表方法、高效记忆法、合作学习法等方法学习地理知识,增加学习能力。[幻灯片] “3S技术”的应用:地理信息技术的应用十分广泛,从实际身旁的社会生产生活,到地理学的区域地理环境研究。学生的年龄和认知范围决定,此部分的案例教学的运用,前者容易接触到、简单直观、易区分掌握“3S”技术特点和具体应用。而后者涉及地理学科的综合性和区域性的特点,难度较大。针对学情特点,我多以前者案例入手学习,以后者案例加以补充。案例:遥感:(1)视频 专家解说卫星遥感受灾影象(2)教材 图1.6 1998年8月28日洞庭湖及荆江地区卫星遥感图像(3)视频 2008年5月13日“北京一号”卫星提供汶川的灾区遥感图像(4)教材 阅读 遥感在农业方面的应用

大班社会教案:社会公开课关爱你我他
2、我们每个小朋友都有一个健康的身体,小朋友,你们想一想,这些残疾儿童和我们健康的儿童相比在生活中会遇到什么困难或是痛苦的事情?幼儿:眼睛不好的小朋友看不到美丽的世界。聋哑儿童听不到美妙的声音。手脚不好的儿童不能自己穿衣服,裤子不能和我们一样跳舞,游戏。………………3、如果你在生活中看到了残疾儿童,你会怎么样帮助他?幼儿:他们坐轮椅我会推他们去玩、我会扶他们上楼梯、我长大有钱一定会给他们些让他们过上幸福快乐的日子……教师:我们小朋友说的太好了,社会上的人也在关注这些残疾儿童。

大班社会教案:从古到今话交通(一堂公开课)
二、课前准备:1、在教师的指导下,让同学们按自己的兴趣,分成六个小组,参考教材提示的相关内容的学习方法搜集资料。分组情况:陆上交通小组(一至四组):分别查找有关路、桥、陆上交通工具(自行车组、机动车组)发展变化的资料。水上交通小组:查找有关船的发展变化的资料。空中交通小组:查找有关热气球、飞艇、飞机等飞行器发展变化的资料。 2、教师准备相应课件与资料。

幼儿园中班社会教案:乘坐公共汽车
2、了解公共汽车给人带来了很多的方便。3、体验乘坐公共汽车的快乐。活动准备:与客运站联系好、幼儿带好一元钱。活动过程:一、带领幼儿来到站台,体验乘车。1、等候汽车的到来,提醒幼儿要遵守站台秩序,上车先下后上或前门上后门下的道理。2、指导幼儿有序上车及投币上车。3、注意乘车礼貌,给老人及抱小孩的人让座。

中班语言课件教案: 蒲公英妈妈和小蚂蚁
2、进一步培养幼儿的口语表达能力。二、活动准备: 背景图一张;磁性教具:四只蚂蚁 树叶 小船 一条大青虫 四个小伞兵;蚂蚁头饰数量和幼儿人数一样多;蒲公英、青虫头饰各一个;配乐故事磁带。活动过程:(一)出示“蚂蚁”,引出主题。1、看,它是谁?(小蚂蚁)你们喜欢小蚂蚁吗?2、今天我就来讲一个小蚂蚁的故事。故事的名字叫蒲公英妈妈和小蚂蚁。(二)欣赏故事《蒲公英妈妈和小蚂蚁》。1、教师有表情的讲述故事。讲述故事后提问:1)故事的名字叫什么?2)故事里有谁和谁?2、出示背景图,教师边演示教具边讲故事。讲述过程中提问:1)小河的对岸住着谁?2)一阵大风吹来,小蚂蚁坐的树叶小船怎么了?3)野地里有什么?它是什么样子的?4)蒲公英是怎样对待小蚂蚁的?5)小蚂蚁说了些什么?蒲公英妈妈又说了些什么?6)蒲公英妈妈为什么很感激小蚂蚁?7)小蚂蚁是怎样回到自己家的?8)这个故事告诉了我们一个什么道理?

公开课数学活动:我给他们排排队课件教案
2、尝试通过自己的排序活动,体验操作的乐趣。活动准备:项链一串、有规律的事物、幼儿在排序方面的生活经验以及开放性的材料活动过程:一、感受规律的存在,发现生活中的规律。教师出时传好的项链,进行提问:1、漂亮吗?为什么?2、在项链上你还发现了什么?3、它是按照什么规律串起来的?4、如果你来串,你会怎样做?二、引导幼儿联想生活中有规律的事物,使幼儿感受到规律在生活中是无处不在的。

部编版语文八年级上册《愚公移山》教案
3.结合课文说说智叟的形象特征。明确:智叟是一个自作聪明,鼠目寸光,安于现状,胸无大志的人。4.智叟的笑和质疑与愚公妻子的“献疑”有什么不同?明确:这两个人物所说的话,表面上有相似之处,但目的全然不同。愚公之妻是关心,她提问题,是从“献疑”的角度说的。“以君之力”带有关心的语气,“曾不能损魁父之丘,如太行、王屋何”,语气较轻,说的是她的真实想法。但她并不反对移山,所以接着就提出移山过程中必须解决的一个重要问题:“焉置土石?”智叟则显然是讥笑和责难愚公,阻止愚公移山,“甚矣,汝之不惠”是很严厉的责备口气,“残年余力”又显得十足的轻视,“曾不能毁山之一毛”是有意挖苦、讥笑和嘲讽,“其如土石何”反问语气很重。在智叟的眼里,愚公完全是一个愚蠢至极、不可救药的老头。

人教部编版语文八年级上册愚公移山教案
阴阳原是指日光的向背,向日为阳,背日为阴。我国古代地名中的“阴”和“阳”实际上是一种方位指示,“日之所照曰阳”,也就是说太阳所能照到的地方就称为阳。 山水阴阳是说古代以山南、水北为阳,以山北、水南为阴。 形成这种局面的原因是山峰高耸,日光能照射到的地方是山的南面;而河流位于地平面以下,所以太阳能照射到的地方其实是河流的北面。 故有“山南水北谓之阳,山北水南谓之阴”的说法。在我国历史上,很多地名及地理表述都与此关系密切,如江阴、衡阳、汉阳等。 《愚公移山》 中说:“指通豫南,达于汉阴。” 其中的“汉阴”是指汉水的南岸。 “泰山之阳,汶水西流;其阴,济水东流”(姚鼐《登泰山记》)、“所谓华山洞(南宋王象之《舆地纪胜》写为‘华阳洞’。 看正文下句,应为‘华阳洞’)者,以其乃华山之阳名之也”

关于某公司关于档案管理工作的总结报告
七、对辖内机构指导、监督、检查情况一是抓制度建设。指导系统各级参照集团公司档案管理制度,结合辖内工作实际,及时制定完善本机构档案管理制度,明确档案管理的机构、职责、归档范围、归档时间,规范档案的整理、归档、保管、利用以及鉴定、销毁、移交等各环节工作,确保档案工作有据可依。同时,要求系统各级根据国家法律法规变动情况以及工作实际需要,及时修订完善本机构档案管理制度。二是抓队伍建设。要求系统各级高度重视档案人员队伍建设,注重优化档案队伍年龄结构、学历结构,及时将能力强、作风好、业务熟的干部员工充实到本机构档案管理岗位,为档案工作提供坚实可靠的队伍保障。同时,指导系统各级高度重视档案人员能力提升工作,主动加强与当地档案管理部门的联系、沟通和对接,主动接受当地档案管理部门的业务指导,积极参加各类培训和学习,推动自身档案管理工作不断规范。

初中数学人教版二元一次方程组教学设计教案
(一)例题引入篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?方法一:(利用之前的知识,学生自己列出并求解)解:设剩X场,则负(10-X)场。方程:2X+(10-X)=16方法二:(老师带领学生一起列出方程组)解:设胜X场,负Y场。根据:胜的场数+负的场数=总场数 胜场积分+负场积分=总积分得到:X+Y=10 2X+Y=16

小学数学人教版六年级下册《第三课式与方程》教案说课稿
1.整理用字母表示数。(1)梳理知识:用字母表示数量关系:师:用字母可以表示什么?生:用字母表示运算定律用字母表示计算公式用字母表示计算方法师:你能举例说明吗?生:字母表示 数量关系路程=速度×时间 s=vt总价=单价×数量 c=an工作总量=工作效率×工作时间 c=at(2)字母表示计算方法:+=(3)用字母表示计算公式。师:用字母可以表示哪些平面图形的计算公式生:长方形 周长 c=(a+b) ×2 面积:s=ab 正方形 周长 c=4a 面积:s=a2 平行四边形 面积 s =ah三角形 面积 s=ah¸2 梯形 面积 s=(a+b)·h¸2 圆 周长c=πd=2πr 面积 s=πr2(4)用字母表示运算定律加法交换律 a+b=b+a 加法结合律 (a+b)+c=a+(b+c)乘法交换律 a×b=b×a乘法结合律 (a×b)×c=a×(b×c)乘法分配律 (a+b)×c=a×c+b×c2.在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意的问题。师:在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?生交流:(1)在含有字母的式子里,数和字母中间的乘号可以用“?”代替,也可以省略不写。(2)省略乘号时,应当把数写在字母的前面。(3)数与数之间的乘号不能省略。加号、减号、除号都不能省略。3. 典题训练(1)填一填。①李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电( )千瓦时。②如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。③小明今年m 岁,妈妈的岁数比她的3倍少6岁。妈妈的岁数是( )岁。如果m=12,妈妈今年是( )岁。④三个连续的自然数,最大的一个是n,那么最小的一个数是( )。(2)连 一 连。比a多3的数 a3比a少3的数 3a3个a相加的和 a+33个a相乘的积 a-3a的3倍 a的

北师大初中数学九年级上册一元二次方程的解及其估算2教案
探索1:上节我们列出了与地毯的花边宽度有关的方程。地毯花边的宽x(m),满足方程 (8―2x)(5―2x)=18也就是:2x2―13x+11=0你能估算出地毯花边的宽度x吗?(1)x可能小于0吗?说说你的理由;_____________________________.(2)x可能大于4吗?可能大于2.5吗?为什么?(3)完成下表x 0 0.5 1 1.5 2 2.52x2-13x+11 (4)你知道地毯花边的宽x(m)是多少吗?还有其他求解方法吗?与同伴交流。探索2:梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,也就是x2+12x―15=0(1)你能猜出滑动距离x(m)的大致范围吗?(2)x的整数部分是_____?十分位是_______?x 0 x2+12x-15 所以 ___<x<___进一步计算x x2+12x-15 所以 ___<x<___因此x 的整数部分是___,十分位是___.三、当堂训练:完成课本34页随堂练习四、学习体会:五、课后作业

北师大初中数学九年级上册一元二次方程2教案
三、课堂检测:(一)、判断题(是一无二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)1. 5x2+1=0 ( ) 2. 3x2+ +1=0 ( )3. 4x2=ax(其中a为常数) ( ) 4.2x2+3x=0 ( )5. =2x ( ) 6. =2x ( ) (二)、填空题.1.方程5(x2- x+1)=-3 x+2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.2.如果方程ax2+5=(x+2)(x-1)是关于x的一元二次方程,则a__________.3.关于x的方程(m-4)x2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程。四、学习体会:五、课后作业

人教版新课标小学数学五年级上册简易方程教案2篇
(1) 你是用什么方法解方程的?要求学生独立完成。请一位同学在黑板上计算。学生交流:等式的两边同时加上同一个数,等式仍然成立。也就是方程 x-9=15的两边同时加上9,抵消掉等式左边的9,这样等式的左边只剩下x。(2) 你会检验方程的解是否正确吗?指导学生把方程的解代入方程进行检验。2.出示:64页第2题的第2小题。提问:你是根据哪个等量关系列出方程的?(1) 标准体重+超出标准的重量=胖胖的体重(2) 标准体重-低于标准的重量=小明的体重提问:他们标准体重的计算方法有什么不同?学生交流:一个是等式两边同时减去同一个数,一个是等式两边同时加上同一个数。三、拓宽应用。1.解方程:x-5.3=10 75-x=402.65页第4题提问:你是怎样选出各方程的解的?把未知数的值代入方程,看看左右是否相等。3.65页第5题提示学生认真读题,注意选择题中所给出的条件是否有用。

人教版新课标小学数学三年级下册位置与方向教案2篇
【教学目标】1、知识目标:结合具体情境,使学生认识东、南、西、北四个方向,能够用给定的一个方向辨认其余的三个方向,并能用这些词语描述物体所在的方位。2、能力目标:培养学生良好的观察能力和空间想象能力。3、情感目标:体验数学与现实生活的密切关系,增强学生学数学、用数学的意识。【教学重难点】使学生认识东、南、西、北四个方向,并能根据学生自身的方位辨认东、南、西、北这四个方向。【教学准备】1、挂图、指南针2、学具准备:准备主题图中相关的学具卡片或实物。【教学过程】一、创设情境,引入新知:同学们,你们想去北京吗?今天我们去参观参观吧?二、愉快体验,探究新知1、认识方向:出示主题图:我们来到了北京的天安门广场,你们看见了哪些建筑物?愿意当小导游为大家介绍一个吗?(先同桌之间互相练习解说,师出示教学挂图,介绍天安门的地理位置)引出例1)

北师大初中数学九年级上册正方形的性质1教案
在Rt△ABC中,AC=AB2+BC2=12+12=2(cm),∴FC=AC-AF=2-1(cm),∴BE=2-1(cm).方法总结:正方形被对角线分成4个等腰直角三角形,因此在正方形中解决问题时常用到等腰三角形的性质与直角三角形的性质.【类型三】 利用正方形的性质证明线段相等如图,已知过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.解析:由PE⊥BC,PF⊥CD知四边形PECF为矩形,故有EF=PC,这时只需说明AP=CP,由正方形对角线互相垂直平分可知AP=CP.证明:连接AC,PC,如图.∵四边形ABCD为正方形,∴BD垂直平分AC,∴AP=CP.∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴PC=EF,∴AP=EF.方法总结:(1)在正方形中,常利用对角线互相垂直平分证明线段相等;(2)无论是正方形还是矩形,经常连接对角线,这样可以使分散的条件集中.

北师大初中九年级数学下册二次函数与一元二次方程2教案
教学目标:1.知道二次函数与一元二次方程的联系,提高综合解决问题的能力.2.会求抛物线与坐标轴交点坐标,会结合函数图象求方程的根.教学重点:二次函数与一元二次方程的联系.预设难点:用二次函数与一元二次方程的关系综合解题.☆ 预习导航 ☆一、链接:1.画一次函数y=2x-3的图象并回答下列问题(1)求直线y=2x-3与x轴的交点坐标; (2)解方程2x-3=0(3)说出直线y=2x-3与x轴交点的横坐标和方程根的关系2.不解方程3x2-2x+4=0,此方程有 个根。二、导读画二次函数y= x2-5x+4的图象1.观察图象,抛物线与x轴的交点坐标是什么?2.求一元二次方程x2-5x+4=0的解。3.抛物线与x轴交点的横坐标与一元二次方程x2-5x+4=0的解有什么关系?(3)一元二次方程ax2+bx+c=0是二次函数y=ax2+bx+c当函数值y=0时的特殊情况.二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?

北师大初中七年级数学上册从三个方向看物体的形状教案1
1.经历从不同方向观察物体的活动过程,发展空间观念.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的形状.3.能识别从三个方向看到的简单物体的形状,会画立方体及简单组合体从三个方向看到的形状,并能根据看到的形状描述基本几何体或实物原型.一、情境导入观察图中不同方向拍摄的庐山美景.你能从苏东坡《题西林壁》诗句:“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”体验出其中的意境吗?你能挖掘出其中蕴含的数学道理吗?让我们一起探索新知吧!二、合作探究探究点一:从不同的方向看物体如图所示的几何体是由一些小正方体组合而成的,从上面看到的平面图形是()解析:这个几何体从上面看,共有2行,第一行能看到3个小正方形,第二行能看到2个小正方形.故选D.
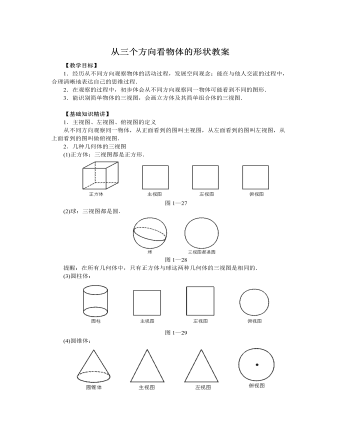
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

