-

北师大初中七年级数学上册数据的收集教案1
新建成的红星中学,首次招收七年级新生12个班共500人,学校准备修建一个自行车车棚.请问需要修建多大面积的自行车车棚?请你设计一个调查方案解决这个问题.解析:决定自行车车棚面积的因素有两个,即自行车的数量与每辆自行车的占地面积.因此收集数据的重点应围绕这两个因素进行.解:调查方案如下:(1)对全体新生的到校方式进行问卷调查.调查问卷如下:你到校的方式是骑自行车吗?A.经常是 B.不经常是C.很少是 D.从不是(2)根据调查问卷结果分类统计骑自行车的人数;(3)实际测量或估计存放1辆自行车的大约占地面积;(4)根据学校的建设规划、财力等因素确定自行车车棚的面积.方法总结:确定调查方案时必须明确两个问题:(1)需要收集哪些数据?(2)采用什么方式进行调查可以获得这些数据?探究点三:从图表中获取信息小冰就公众对在餐厅吸烟的态度进行了调查,并将调查结果制作成如图所示的统计图,请根据图中的信息回答下列问题:

北师大初中七年级数学下册积的乘方教案
【类型一】 逆用积的乘方进行简便运算计算:(23)2014×(32)2015.解析:将(32)2015转化为(32)2014×32,再逆用积的乘方公式进行计算.解:原式=(23)2014×(32)2014×32=(23×32)2014×32=32.方法总结:对公式an·bn=(ab)n要灵活运用,对于不符合公式的形式,要通过恒等变形转化为公式的形式,运用此公式可进行简便运算.【类型二】 逆用积的乘方比较数的大小试比较大小:213×310与210×312.解:∵213×310=23×(2×3)10,210×312=32×(2×3)10,又∵23<32,∴213×310<210×312.方法总结:利用积的乘方,转化成同底数的同指数幂是解答此类问题的关键.三、板书设计1.积的乘方法则:积的乘方等于各因式乘方的积.即(ab)n=anbn(n是正整数).2.积的乘方的运用在本节的教学过程中教师可以采用与前面相同的方式展开教学.教师在讲解积的乘方公式的应用时,再补充讲解积的乘方公式的逆运算:an·bn=(ab)n,同时教师为了提高学生的运算速度和应用能力,也可以补充讲解:当n为奇数时,(-a)n=-an(n为正整数);当n为偶数时,(-a)n=an(n为正整数)

北师大初中七年级数学下册幂的乘方教案
方法总结:本题考查了幂的乘方的逆用及同底数幂的乘法,整体代入求解也比较关键.【类型三】 逆用幂的乘方结合方程思想求值已知221=8y+1,9y=3x-9,则代数式13x+12y的值为________.解析:由221=8y+1,9y=3x-9得221=23(y+1),32y=3x-9,则21=3(y+1),2y=x-9,解得x=21,y=6,故代数式13x+12y=7+3=10.故答案为10.方法总结:根据幂的乘方的逆运算进行转化得到x和y的方程组,求出x、y,再计算代数式.三、板书设计1.幂的乘方法则:幂的乘方,底数不变,指数相乘.即(am)n=amn(m,n都是正整数).2.幂的乘方的运用幂的乘方公式的探究方式和前节类似,因此在教学中可以利用该优势展开教学,在探究过程中可以进一步发挥学生的主动性,尽可能地让学生在已有知识的基础上,通过自主探究,获得幂的乘方运算的感性认识,进而理解运算法则

北师大初中七年级数学下册频率的稳定性教案
解析:(1)根据表中信息,用优等品频数m除以抽取的篮球数n即可;(2)根据表中数据,优等品频率为0.94,0.95,0.93,0.94,0.94,稳定在0.94左右,即可估计这批篮球优等品的概率.解:(1)570600=0.95,744800=0.93,9401000=0.94,11281200=0.94,故表中依次填0.95,0.93,0.94,0.94; (2)这批篮球优等品的概率估计值是0.94.三、板书设计1.频率及其稳定性:在大量重复试验的情况下,事件的频率会呈现稳定性,即频率会在一个常数附近摆动.随着试验次数的增加,摆动的幅度有越来越小的趋势.2.用频率估计概率:一般地,在大量重复实验下,随机事件A发生的频率会稳定到某一个常数p,于是,我们用p这个常数表示随机事件A发生的概率,即P(A)=p.教学过程中,学生通过对比频率与概率的区别,体会到两者间的联系,从而运用其解决实际生活中遇到的问题,使学生感受到数学与生活的紧密联系

北师大初中七年级数学下册平行线的性质教案
解析:平行线中的拐点问题,通常需过拐点作平行线.解:(1)∠AED=∠BAE+∠CDE.理由如下:过点E作EG∥AB.∵AB∥CD,∴AB∥EG∥CD,∴∠AEG=∠BAE,∠DEG=∠CDE.∵∠AED=∠AEG+∠DEG,∴∠AED=∠BAE+∠CDE;(2)同(1)可得∠AFD=∠BAF+∠CDF.∵∠BAF=2∠EAF,∠CDF=2∠EDF,∴∠BAE+∠CDE=32∠BAF+32∠CDF,∴∠AED=32∠AFD.方法总结:无论平行线中的何种问题,都可转化到基本模型中去解决,把复杂的问题分解到简单模型中,问题便迎刃而解.三、板书设计平行线的性质:性质1:两条平行线被第三条直线所截,同位角相等;性质2:两条平行线被第三条直线所截,内错角相等;性质3:两条平行线被第三条直线所截,同旁内角互补.平行线的性质是几何证明的基础,教学中注意基本的推理格式的书写,培养学生的逻辑思维能力,鼓励学生勇于尝试.在课堂上,力求体现学生的主体地位,把课堂交给学生,让学生在动口、动手、动脑中学数学

北师大初中七年级数学下册图形的全等教案
解析:根据“全等三角形的对应角相等”,可知∠EAD=∠CAB,故∠EAB=∠EAD+∠CAD+∠CAB=2∠CAB+10°=120°,即∠CAB=55°.然后在△ACB中利用三角形内角和定理来求∠ACB的度数.解:∵△ABC≌△ADE,∴∠CAB=∠EAD.∵∠EAB=120°,∠CAD=10°,∴∠EAB=∠EAD+∠CAD+∠CAB=2∠CAB+10°=120°,∴∠CAB=55°.∵∠B=∠D=25°,∴∠ACB=180°-∠CAB-∠B=180°-55°-25°=100°.方法总结:本题将三角形内角和与全等三角形的性质综合考查,解答问题时要将所求的角与已知角通过全等及三角形内角之间的关系联系起来.三、板书设计1.全等形与全等三角形的概念:能够完全重合的图形叫做全等形;能够完全重合的三角形叫做全等三角形.2.全等三角形的性质:全等三角形的对应角、对应线段相等.首先展示全等形的图片,激发学生兴趣,从图中总结全等形和全等三角形的概念.最后总结全等三角形的性质,通过练习来理解全等三角形的性质并渗透符号语言推理.通过实例熟悉运用全等三角形的性质解决一些简单的实际问题

北师大初中数学九年级上册矩形的判定1教案
在△AEF和△DEC中,∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,∴△AEF≌△DEC(AAS),∴AF=DC.∵AF=BD,∴BD=DC;(2)当△ABC满足AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形.∴AB=AC,BD=DC,∴∠ADB=90°.∴四边形AFBD是矩形.方法总结:本题综合考查了矩形和全等三角形的判定方法,明确有一个角是直角的平行四边形是矩形是解本题的关键.三、板书设计矩形的判定对角线相等的平行四边形是矩形三个角是直角的四边形是矩形有一个角是直角的平行四边形是矩形(定义)通过探索与交流,得出矩形的判定定理,使学生亲身经历知识的发生过程,并会运用定理解决相关问题.通过开放式命题,尝试从不同角度寻求解决问题的方法.通过动手实践、合作探索、小组交流,培养学生的逻辑推理能力.

北师大初中数学九年级上册菱形的性质2教案
1. _____________________________________________2. _____________________________________________你会计算菱形的周长吗?三、例题精讲例1.课本3页例1例2.已知:在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=OH.四、课堂检测:1.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,菱形的边长是________cm.2.菱形ABCD的周长为40cm,两条对角线AC:BD=4:3,那么对角线AC=______cm,BD=______cm.3.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 4.已知菱形的面积为30平方厘米,如果一条对角线长为12厘米,则别一条对角线长为________厘米.5.菱形的两条对角线把菱形分成全等的直角三角形的个数是( ).(A)1个 (B)2个 (C)3个 (D)4个6.在菱形ABCD中,CE⊥AB,E为垂足,BC=2,BE=1,求菱形的周长和面积

北师大初中数学九年级上册菱形的判定2教案
方法三:一个同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?请你画一画。通过探究,得到: 的四边形是菱形。证明上述结论:三、例题巩固课本6页例2 四、课堂检测1、下列判别错误的是( )A.对角线互相垂直,平分的四边形是菱形. B、对角线互相垂直的平行四边形是菱形C.有一条对角线平分一组对角的四边形是菱形. D.邻边相等的平行四边形是菱形.2、下列条件中,可以判定一个四边形是菱形的是( )A.两条对角线相等 B.两条对角线互相垂直C.两条对角线相等且垂直 D.两条对角线互相垂直平分3、要判断一个四边形是菱形,可以首先判断它是一个平行四边形,然后再判定这个四边形的一组__________或两条对角线__________.4、已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F求证:四边形AFCE是菱形

北师大初中数学九年级上册菱形的判定1教案
(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC.又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形.又∵EF=BE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为23,∴菱形的面积为4×23=83.方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.三、板书设计菱形的判 定有一组邻边相等的平行四边形是菱形(定义)四边相等的四边形是菱形对角线互相垂直的平行四边形是菱形对角线互相垂直平分的四边形是菱形 经历菱形的证明、猜想的过程,进一步提高学生的推理论证能力,体会证明过程中所运用的归纳概括以及转化等数学方法.在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.

幼儿园中班安全教案:阳台上的安全
活动过程1、幼儿根据已有经验谈谈阳台的主要功能。"小朋友家里是不是都有阳台?你们都在阳台上做些什么?"小结:阳台是一个伸向屋外的平台,它可以接触到更多的空气和阳光。有的人家在阳台上晒衣服,养花,养鱼,有的人在阳台上活动身体,锻炼。夏天,还可在阳台上乘凉。大家都需要它。2、观看录像,讨论在阳台上哪些行为是对的,哪些是错误的。片段一:小朋友在阳台上看书、折纸。片段二:小朋友在阳台上锻炼身体。片段三:一幼儿将头和身体伸向阳台外喊楼下的小朋友。片段四:一幼儿往阳台外抛东西。片段五:一幼儿将身体伸向阳台外拿手帕。片段六:一小朋友在阳台上玩,忽然风将阳台门吹上了,怎么办?教师引导幼儿分段观看录像片,每看完一段,建议提问:这位小朋友的行为哪里对,哪里错,为什么?应该怎样做?

幼儿园中班安全教案:有趣的交通标志
活动准备:各种交通标志、画有标志或无标志的拼板若干、立体骰子若干、带有交通标志的礼物若干、磁带、录音机、有交通标志的牌子 活动过程: 一、 随音乐跳兔子舞进入活动场地。二、 你说我翻 “小朋友,你们知道哪些交通标志啊?你们所说的可能会在后面的黑板上哦!”

幼儿园中班安全教案:安全、愉快的过假期
考虑到幼儿未真正懂得暑假的含义,于是,在活动的前端,便设计了让幼儿了解“暑假”这个词语的含义。以便在接下来的活动中,让幼儿对暑假这个词汇容易理解和接受。由于幼儿大多是在家里过暑假,这便需要家长对安全知识有深刻的认识,需要家长认真配合做好安全教育工作。于是,我便设计了让家长填写一份《暑假安全知识调查表》,借助家长的力量帮助加强孩子们的安全意识。活动目标:1、使幼儿了解暑假中应注意的安全和卫生,增强幼儿的自我保护意识。2、通过讨论,激发幼儿向往过暑假的情感,教育幼儿愉快、合理地过暑假。3、培养幼儿完整、连贯地表达能力和对事物的判断能力。
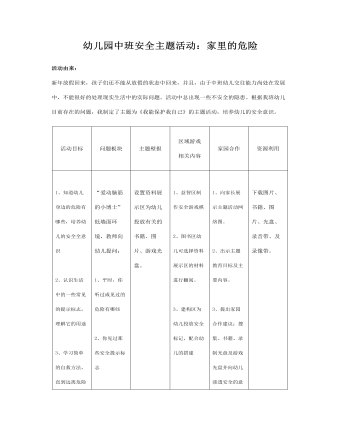
中班安全主题活动教案:家里的危险
1、知道幼儿身边的危险有哪些,培养幼儿的安全全意识2、认识生活中的一些常见的提示标志,理解它的用途3、学习简单的自救方法,直到远离危险

幼儿园中班健康教案:谁的牙齿最干净
2、通过观察阅读画面,初步认识牙齿的好坏,了解刷牙的正确方法。 3、懂得牙齿的用处很大,要注意保护好自己的牙齿。 活动准备: 洗好、切好的苹果若干 幼儿用书——我的牙齿用处大,铅笔人手一支。 活动过程: 1、每一位小朋友吃一块苹果,说说牙齿的用处。 教师:请小朋友慢慢吃苹果,吃完后告诉大家,你是怎样把苹果吃下去的? 引导幼儿说出需要牙齿咬和嚼,帮助我们把食物吃下去。 2、认识牙齿的构造。 请小朋友把嘴巴张开,互相看一看,牙齿是什么样子的? 使幼儿知道每个人嘴巴里有许多牙齿,我们的牙齿有上下两排,嘴里牙齿的形状和大小不一样,牙齿是白白的 3、组织幼儿讨论:牙齿有什么用? (1)、鼓励幼儿根据自己以有的知识经验,大胆地参与讲述活动。通过讨论使幼儿知道牙齿可以帮助我们将大块的食物嚼碎变成小块的食物。 (2)、启发幼儿想一想:牙齿除了可以帮助我们吃食物,他还有什么作用呢? 教师请小朋友先试一试发“四”这个音,让幼儿感受到,如果没有牙齿不能发出“四”,再试一试发“师”、“自己”等音,没有牙齿行吗? 小结:牙齿还可以帮助我们讲话,帮助我们发准音。 组织幼儿讨论:怎样保护自己的牙齿呢? 教师小结:每天早晚要漱口、刷牙。睡觉前,不吃零食、少吃甜食和坚硬的食物。

幼儿园中班健康教案:保护我们的皮肤
2、通过观察,了解皮肤,注意保护皮肤的清洁并使皮肤尽量不受到损伤。 3、能大胆地在集体面前表述自己的想法。 活动准备 1、教学挂图一张。 2、放大镜人手一个。 活动过程 1.通过提问,引导幼儿观察认识皮肤。 (1)教师:你们知道我们身体最外面一层表皮是什么吗?请你找一找,我们身体的哪些地方有皮肤? (2)观察认识皮肤。 提问:皮肤摸上去有什么感觉?皮肤看上去是什么样子的?皮肤上有什么?(汗毛)用放大镜看一看,皮肤又是什么样子的?你的皮肤是什么颜色的,你见过什么颜色的皮肤? 出示挂图,观察皮肤的剖面图以及不同肤色的儿童,直观感受皮肤组织的构成和不同人种的肤色。

幼儿园中班歌唱教案:迷路的小花鸭
2、尝试创编歌词及制作图谱,体验歌唱活动的乐趣。 3、感受人与动物间和谐美好的关系,培养幼儿关心、爱护小动物的情感。二、活动准备: 图片《迷路的小花鸭》(一)(二),图谱(一)(二),哭笑脸谱各一个。三、活动过程: 1、练声:我爱我的小动物(5个音阶) (评析:开始部分的练声,既是为下面的歌唱活动作好准备,同时,也让幼儿在歌唱喜爱的小动物时自然地表达对动物的热爱之情。) 2、故事导入,激发幼儿的兴趣。 出示图片(一),师:你看到了什么? 幼A:我看到有一天,一只小鸭子在池塘边玩。 幼B:我看到小鸭子哭了。因为它想妈妈了。 幼C:我还看到了柳树。 师讲述故事:有一天,小花鸭在池塘边的柳树下玩,玩着玩着它迷路了,找不到家也找不到妈妈了,它哭了,哭着喊着叫它的妈妈。 (评析:这是一个开放性的问题,它打破了传统提问“这是什么地方?有谁?”等问题带来的局限性,它使幼儿能充分表达他们对画面意思的理解,使图片变活,也便于幼儿理解教师讲述的故事。)

北师大初中数学九年级上册比例的性质2教案
请写出 推理过程:∵ ,在两边同时加上1得, + = + .两边分别通分得: 思考:请仿照上面的方法,证明“如果 ,那么 ”.(3) 等比性质:猜想 ( ),与 相等吗?能 否证明你的猜想?(引导学生从上述实例中找出证明方法)等比性质:如果 ( ),那么 = .思考:等比性质中,为什么要 这个条件?三、 巩固练习:1.在相同时刻的物高与影长成比例,如果一建筑在地面上影长为50米,高为1.5米的测竿的影长为2.5米 ,那么,该建筑的高是多少米?2.若 则 3.若 ,则 四、 本课小结:1.比例的基本性质:a:b=c:d ;2. 合比性质:如果 ,那么 ;3. 等比性质:如果 ( ),五、 布置作业:课本习题4.2

北师大初中七年级数学上册数据的收集教案2
1. 小明的脚长23.6厘米,鞋号应是 号。2.小亮的脚长25.1厘米,鞋号应是 号。3.小王选了25号鞋,那么他的脚长约是大于等于 厘米且小于 厘米。小结:刚才同学们都体会到了分组编码使原来繁多,无叙的数据简化、有序。因此分组、编码是整理数据的一种重要的方法,在工商业、科研等活动中有广泛的应用(四)反馈练习课内练习以下是某校七年级南,女生各10名右眼裸视的检测结果:0.2,0.5,0.7(女),1.0,0.3(女),1.2(女),1.5,1.2,1.5(女),0.4(女),1.5,1.1,1.2(女),0.8(女),1.5(女),0.6(女),1.0(女),0.8,1.5,1.2(1)这组数据是用什么方法获得的?(2)学生右眼视力跟性别有关吗?为了回答这个问题,你将怎样处理这组数据?你的结论是什么?(五). 归纳小结,体味数学快乐通过本节课的学习,你有那些收获?(课堂小结交给学生)数据收集的方法:直接观察、测量、调查、实验、查阅文献资料、使用互连网等。整理数据的方法:分类、排序、分组编码等。(学生可能还会指出鞋码和脚长之间的关系等)

北师大初中八年级数学下册不等式的解集教案
【类型二】 根据数轴求不等式的解关于x的不等式x-3<3+a2的解集在数轴上表示如图所示,则a的值是()A.-3 B.-12 C.3 D.12解析:化简不等式,得x<9+a2.由数轴上不等式的解集,得9+a=12,解得a=3,故选C.方法总结:本题考查了在数轴上表示不等式的解集,利用不等式的解集得关于a的方程是解题关键.三、板书设计1.不等式的解和解集2.用数轴表示不等式的解集本节课学习不等式的解和解集,利用数轴表示不等式的解,让学生体会到数形结合的思想的应用,能够直观的理解不等式的解和解集的概念,为接下来的学习打下基础.在课堂教学中,要始终以学生为主体,以引导的方式鼓励学生自己探究未知,提高学生的自我学习能力.