-

北师大初中数学九年级上册一元二次方程的根与系数的关系2教案
3、一般地,对于关于 方程 为已知常数, ,试用求根公式求出它的两个解x1、x2,算一算x1+x2、x1?x2的值,你能得出什么结果?与上面发现的现象是否一致。【知识应用】 1、(1)不解方程,求方程两根的和两根的积:① ② (2)已知方程 的一个根是2,求它的另一个根及 的值。(3)不解方程,求一 元二次方程 两个根的①平方和;②倒数和。(4)求一元二次方程,使它的两个根是 。【归纳小结】【作业】1、已知方程 的一个根是1,求它的另一个根及 的值。2、设 是方程 的两个根,不解方程,求下列各式的值。① ;② 3、求一个一元次方程,使它的两 个根分别为:① ;② 4、下列方程两根的和与两根的积各是多少 ?① ; ② ; ③ ; ④ ;

北师大初中数学九年级上册用公式法求解一元二次方程2教案
二、填空题1.一元二次方程ax2+bx+c=0(a≠0)的求根公式是________,条件是________.2.当x=______时,代数式x2-8x+12的值是-4.3.若关于x的一元二次方程(m-1)x2+x+m2+2m-3=0有一根为0,则m的值是_____.三、综合提高题1.用公式法解关于x的方程:x2-2ax-b2+a2=0.2.设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,(1)试推导x1+x2=- ,x1·x2= ;(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.3.某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时 元收费.(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)(2)下表是这户居民3月、4月的用电情况和交费情况
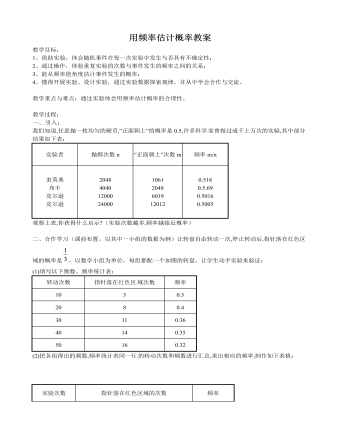
北师大初中数学九年级上册用频率估计概率2教案
(1)填写表格中次品的概率.(2)从这批西装中任选一套是次品的概率是多少?(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装?六、课堂小结:尽管随机事件在每次实验中发生与否具有不确定性,但只要保持实验条件不变,那么这一事件出现的频率就会随着实验次数的增大而趋于稳定,这个稳定值就可以作为该事件发生概率的估计值。七、作业:课后练习补充:一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球与10的比值,再把球放回袋中摇匀。不断重复上述过程5次,得到的白求数与10的比值分别为:0.4,0.1,0.2,0.1,0.2。根据上述数据,小亮可估计口袋中大约有 48 个黑球。

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册用公式法求解一元二次方程2教案
二、填空题1.一元二次方程ax2+bx+c=0(a≠0)的求根公式是________,条件是________.2.当x=______时,代数式x2-8x+12的值是-4.3.若关于x的一元二次方程(m-1)x2+x+m2+2m-3=0有一根为0,则m的值是_____.三、综合提高题1.用公式法解关于x的方程:x2-2ax-b2+a2=0.2.设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,(1)试推导x1+x2=- ,x1·x2= ;(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.3.某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时 元收费.(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)(2)下表是这户居民3月、4月的用电情况和交费情况

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示
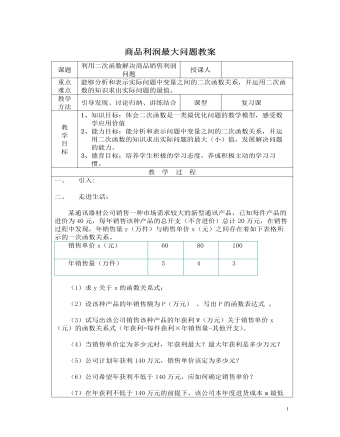
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业

北师大初中九年级数学下册三角函数的计算2教案
解在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.例5 已知cot x=0.1950,求锐角x.(精确到1′)分析根据tan x= ,可以求出tan x的值,然后根据例4的方法就可以求出锐角x的值.四、课堂练习1. 使用计算器求下列三角函数值.(精确到0.0001)sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.2. 已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)(1)sin a=0.2476; (2)cos a=0.4174;(3)tan a=0.1890; (4)cot a=1.3773.五、学习小结内容总结不同计算器操作不同,按键定义也不一样。同一锐角的正切值与余切值互为倒数。在生活中运用计算器一定要注意计算器说明书的保管与使用。方法归纳在解决直角三角形的相关问题时,常常使用计算器帮助我们处理比较复杂的计算。

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?
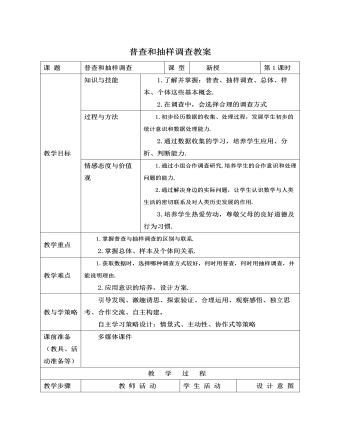
北师大初中七年级数学上册普查和抽样调查教案2
1.举例说明什么时候用普查的方式获得数据较好,什么时候用抽样调查的方式获得数据较好?2、下列调查中分别采用了那些调查方式?⑴为了了解你们班同学的身高,对全班同学进行调查.⑵为了了解你们学校学生对新教材的喜好情况,对所有学号是5的倍数的同学进行调查。3、说明在以下问题中,总体、个体、样本各指什么?⑴为了考察一个学校的学生参加课外体育活动的情况,调查了其中20名学生每天参加课外体育活动的时间.⑵为了了解一批电池的寿命,从中抽取10只进行实验。⑶为了考察某公园一年中每天进园的人数,在其中的30天里对进园的人数进行了统计。通过本节课的学习,同学们有什么收获和疑问?1、基本概念:⑴.调查、普查、抽样调查.⑵.总体、个体、样本.2、何时采用普查、何时采用抽样调查,各有什么优缺点?
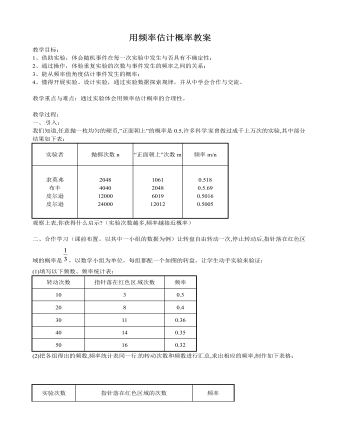
北师大初中数学九年级上册用频率估计概率2教案
(4)议一议:频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何?结论:从上面的试验可以看到:当重复实验的次数大量增加时,事件发 生的频率就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率。三、做一做:1.某运动员投篮5次, 投中4次,能否说该运动员投一次篮,投中的概率为4/5?为什么?2.回答下列问题:(1)抽检1000件衬衣,其中不合格的衬衣有2件,由 此估计抽1件衬衣合格的概率是多少?(2)1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少?
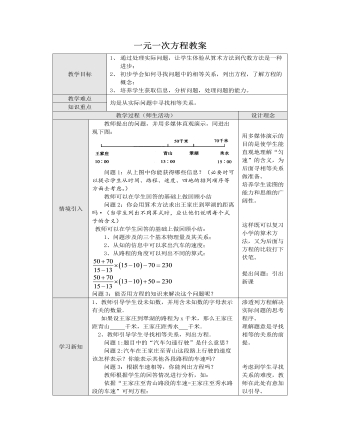
北师大初中七年级数学上册一元一次方程教案2
1、突出问题的应用意识.教师首先用一个学生感兴趣的实际问题引人课题,然后运用算术的方法给出解答。在各环节的安排上都设计成一个个的问题,使学生能围绕问题展开思考、讨论,进行学习.2、体现学生的主体意识.本设计中,教师始终把学生放在主体的地位:让学生通过对列算式与列方程的比较,分别归纳出它们的特点,从而感受到从算术方法到代数方法是数学的进步;让学生通过合作与交流,得出问题的不同解答方法;让学生对一节课的学习内容、方法、注意点等进行归纳.3、体现学生思维的层次性.教师首先引导学生尝试用算术方法解决间题,然后再逐步引导学生列出含未知数的式子,寻找相等关系列出方程.在寻找相等关系、设未知数及作业的布置等环节中,教师都注意了学生思维的层次性.4、渗透建模的思想.把实际间题中的数量关系用方程形式表示出来,就是建立一种数学模型,教师有意识地按设未知数、列方程等步骤组织学生学习,就是培养学生由实际问题抽象出方程模型的能力.

北师大初中七年级数学上册有理数乘法的运算律教案2
分析:(1)(2)用乘法的交换、结合律;(3)(4)用分配律,4.99写成5-0.01学生板书完成,并说明根据什么?略例3、某校体育器材室共有60个篮球。一天课外活动,有3个班级分别计划借篮球总数的 , 和 。请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?解:=60-30-20-15 =-5答:不够借,还缺5个篮球。练习巩固:第41页1、2、7、探究活动 (1)如果2个数的积为负数,那么这2个数中有几个负数?如果3个数的积为负数,那么这3个数中有几个负数?4个数呢?5个数呢?6个数呢?有什么规律? (2)逆用分配律 第42页 5、用简便方法计算(三)课堂小结通过本节课的学习,大家学会了什么?本节课我们探讨了有理数乘法的运算律及其应用.乘法的运算律有:乘法交换律:a×b=b×a;乘法结合律:(a×b)×c=a×(b×c);分配律:a×(b+c)=a×b+a×c.在有理数的运算中,灵活运用运算律可以简化运算.(四)作业:课本42页作业题

北师大初中数学八年级上册二次根式的混合运算2教案
本节课开始时,首先由一个要在一块长方形木板上截出两块面积不等的正方形,引导学生得出两个二次根式求和的运算。从而提出问题:如何进行二次根式的加减运算?这样通过问题指向本课研究的重点,激发学生的学习兴趣和强烈的求知欲望。本节课是二次根式加减法,目的是探索二次根式加减法运算法则,在设计本课时教案时,着重从以下几点考虑:1.先通过对实际问题的解决来引入二次根式的加减运算,再由学生自主讨论并总结二次根式的加减运算法则。2.四人小组探索、发现、解决问题,培养学生用数学方法解决实际问题的能力。3.对法则的教学与整式的加减比较学习。在理解、掌握和运用二次根式的加减法运算法则的学习过程中,渗透了分析、概括、类比等数学思想方法,提高学生的思维品质和兴趣。

北师大初中数学八年级上册认识二元一次方程组2教案
第一环节:情境引入内容:(一) 情境1实物投影,并呈现问题:在一望无际的呼伦贝尔大草原上,一头老牛和一匹小马驮着包裹吃力地行走着,老牛喘着气吃力地说:“累死我了”,小马说:“你还累,这么大的个,才比我多驮2个.”老牛气不过地说:“哼,我从你背上拿来一个,我的包裹就是你的2倍!”,小马天真而不信地说:“真的?!”同学们,你们能否用数学知识帮助小马解决问题呢?请每个学习小组讨论(讨论2分钟,然后发言).教师注意引导学生设两个未知数,从而得出二元一次方程.这个问题由于涉及到老牛和小马的驮包裹的两个未知数,我们设老牛驮x个包裹,小马驮y个包裹,老牛的包裹数比小马多2个,由此得方程 ,若老牛从小马背上拿来1个包裹,这时老牛的包裹是小马的2倍, 得方程: .

北师大初中数学九年级上册反比例函数的应用2教案
补充题:为了预防“非典”,某学校对教室采用药熏消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如右图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后,y关于x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?答案:(1)y= x, 010,即空气中的含药量不低于3毫克/m3的持续时间为12分钟,大于10分钟的有效消毒时间.

北师大初中数学九年级上册正方形的性质2教案
1)正方形的边长为4cm,则周长为( ),面积为( ) ,对角线长为( );2))正方形ABCD中,对角线AC、BD交于O点,AC=4 cm,则正方形的边长为( ), 周长为( ),面积为( )3)在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,OA= ,AC= 。4) 1、正方形具有而矩形不一定具有的性质是( ) A、四个角相等 B、对角线互相垂直平分 C、对角互补 D、对角线相等. 5)、正方形具有而菱形不一定具有的性质( ) A、四条边相等 B对角线互相垂直平分 C对角线平分一组对角 D对角线相等. 6)、正方形对角线长6,则它的面积为_________ ,周长为________. 7)、顺次连接正方形各边中点的小正方形的面积是原正方形面积的( )A.1/2 B.1/3 C.1/4 D.1/ 5四:范例讲解:1、(课本P21例1)学生自己阅读课本内容、注意证明过程的书写2、 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE

北师大初中数学九年级上册一元二次方程的根与系数的关系2教案
2、猜想 一元二次方程的两个根 的和与积和原来的方程有什么联系?小组交流。3、一般地,对于关于 方程 为已知常数, ,试用求根公式求出它的两个解x1、x2,算一算x1+x2、x1?x2的值,你能得出什么结果?与上面发现的现象是否一致。【知识应用】 1、(1)不解方程,求方程两根的和两根的积:① ② (2)已知方程 的一个根是2,求它的另一个根及 的值。(3)不解方程,求一 元二次方程 两个根的①平方和;②倒数和。(4)求一元二次方程,使它的两个根是 。【归纳小结】【作业】1、已知方程 的一个根是1,求它的另一个根及 的值。2、设 是方程 的两个根,不解方程,求下列各式的值。① ;② 3、求一个一元次方程,使它的两 个根分别为:① ;② 4、下列方程两根的和与两根的积各是多少 ?① ; ② ; ③ ; ④ ;

中班语言课件教案:鼠宝宝学外语
2. 理解词:眉开眼笑、调皮。3. 在欣赏、分析过程中感受故事的幽默、诙谐。重点:要求理解鼠妈妈教鼠宝宝学外语的原因。难点:鼠宝宝从不愿学的动态表现到肯学的思想转变过程。环境创设、材料准备:图片设计思路:这个故事生动有趣,诙谐幽默,能激起幼儿的学习兴趣。一开始以照片的形式出现,吸引了幼儿的注意力,让幼儿加深了对鼠宝宝一家的喜爱之情。接着一系列的提问,例:“第二个生的叫什么?”发展了幼儿 <BR><P></P>的想象力和发展性思维能力,接着引导幼儿进入下一环节,当故事将到一半时停止讲述,给幼儿留下了遐想的空间,让幼儿运用已有的知识经验来理解“外语”一词,通过悬念式的提问,激发幼儿的好奇性心和学习欲望。听完故事,通过感受故事中有趣的词句,对幼儿的倾听能力提出了要求。接着教师的提问“为什么鼠宝宝一开始不愿学外语,可后来却抢着说‘学外语真好呢’”?这个问题具有较强的开发性,幼儿可以从多个角度来回答,充分发展了幼儿的思维。同时,很自然地渗透了品德教育,避免了空洞的说教。