-

莞韶对口帮扶指挥部高质量推进招商引资工作综述
以产业链共建促进合作共赢,重点加强大数据电子信息、先进装备制造等产业合作。目前,共建合作园区华南装备园一期已全面实现“六通一平”,园区综合服务中心、污水处理中心、燃气项目等配套服务设施已建成投入使用,表面处理站、新型多功能产业园一期已竣工。已累计引进工业项目87个,计划总投资153.47亿元,包括明阳、南兴、易事特等上市企业。现有规上企业28家,累计完成固定资产投资78.99亿元,其中工业投资累计完成57.08亿元,现正加快推进园区二期、三期建设。截至今年上半年,市主平台现有规上工业企业149家,实现规上工业增加值24.73亿元,同比增长5.1%,增速实现扭负为正。精准施策引凤来,巧借外力促发展。优质的营商环境、畅通的政策服务,吸引了一大批国内知名企业在我市落户发展,有力促进了我市产业转型升级、提质增效,招商引资的丰硕成果在粤北韶关这块沃土上不断开花结果。

莞韶对口帮扶指挥部高质量推进招商引资工作综述
今年7月,走进广东金志利科技股份有限公司二期5万吨产能项目建设现场,只见机械轰鸣、车辆穿梭,工人们有序施工,一派繁忙景象。“项目达产后,销售将不低于10亿元、净利润规模不低于1.5亿元,整体实力和水平将进入行业前十。”刘国兵笑称。该项目自2017年转移至韶关以来,已获得省、市各级奖补共计6848.43万元,其中,莞韶共建政策建厂补助1200万元,贷款贴息523万元。这是莞韶指挥部抢抓产业有序转移机遇,推动重点项目增资扩产的一个生动缩影。今年以来,借省推动产业有序转移的东风,在韶关市委市政府的坚强指导下,莞韶指挥部抓实抓好合作共建这一抓手,积极推动产业有序转移主平台建设,成效初显。建立完善园区帮扶机制、运营管理机制和长效资金保障机制,延续优质企业项目落户莞韶产业园同时叠加享受东莞市给予的建厂补助、租金补助、贷款贴息和平台建设补助等4个1000万元奖补政策。

XX市公共资源交易中心2024年上半年工作总结和下半年工作谋划
(四)强化新技术应用。持续推进大数据分析等新技术在公共资源交易领域的应用,依靠科技创新破解公共资源交易发展中遇到的重大问题和突出矛盾。持续探索“大数据分析系统”“智能电子档案归集系统”“监控视频自动刻录系统”“手机移动端系统”等功能模块建设,推进公共资源交易由“电子交易”向“智慧交易”升级。持续完善不见面、远程异地评标系统建设,不断提升全市公共资源交易电子化水平。(五)加强公共资源交易智慧大数据分析平台在招标投标领域的运用。启用市公共资源交易智慧大数据分析平台,建立公共资源交易数据模型,强化数据融通和价值挖掘,提升交易中心围标串标风险预警及监测能力。(六)加强系统安全防护。开展系统、机房网络的安全检测,在原有平台系统定期维护更新的基础上,全面优化升级信息系统的上云方案,不断满足全市公共资源电子系统安全建设要求。

2024年区公共资源交易中心上半年工作总结和下半年工作计划
一是强化服务理念,创新服务方式,深化作风建设,提高工作效能,进一步增强大局意识、责任意识和服务意识。坚持以优质服务、高效服务为工作标准,以熟练的业务技能、热情的服务态度、规范的服务行为、公正的办事作风和最大的社会效益,树立诚实守信的社会形象,打造优质高效的服务品牌。二是进一步落实交易项目的提前介入、主动服务工作机制,提前、主动与招标人联系,提供政策咨询、程序引导、业务指导等服务,帮助解决招标和采购中遇到的一些困难和问题。(三)坚持奋发进取,突出创新创优,不断创新公共资源交易中心工作。一是积极与上级相关行业主管单位沟通协调,加强投标人交易行为监管,维护公共资源交易市场秩序。二是密切与纪检监察等有关职能部门的沟通联系,加强项目进场交易情况督查,加强对交易各环节监管,及时纠正交易过程中存在的问题,不断提升交易服务水平,努力实现阳光交易。

xx市绿色农业投资开发有限公司2024上半工作总结和下半年工作计划
谋划专项债项目9个,其中:重点项目2个,总投资68.6亿元。目前,已完成9个项目的立项、财政储备库入库等工作;2个重点项目已完成立项、可研批复、财政评审、“三评一案”编制等工作。(五)做好土地种植方面探索,为农业标准化生产,土地规模化流转摸清道路应对市场变化,探索种植红缨子高粱、泛麦8号等优质农作物的种植推广工作。积极与上游终端企业联合合作,打通产业链终端,扩大订单种植,提升技术含量,增加比较效益,形成区域特色,在巩固原有托管土地面积的前提下,不断探索新的多元化合作、管理模式探索路子。(七)稳步推进亿嘉问题楼盘建设积极申报“保交楼”项目资金,妥善化解xx问题楼盘遗留问题,确保群众利益。(八)积极围绕白芝麻、强弱筋小麦、红高粱等特色农产品种植、深加工项目进行谋划,为打造优质农产品和有机农业品牌不断努力

某区公共资源交易中心2024年上半年工作总结和下半年工作计划
(二)提高服务意识,创新服务方式,树立公共资源交易平台良好形象。一是强化服务理念,创新服务方式,深化作风建设,提高工作效能,进一步增强大局意识、责任意识和服务意识。坚持以优质服务、高效服务为工作标准,以熟练的业务技能、热情的服务态度、规范的服务行为、公正的办事作风和最大的社会效益,树立诚实守信的社会形象,打造优质高效的服务品牌。二是进一步落实交易项目的提前介入、主动服务工作机制,提前、主动与招标人联系,提供政策咨询、程序引导、业务指导等服务,帮助解决招标和采购中遇到的一些困难和问题。(三)坚持奋发进取,突出创新创优,不断创新公共资源交易中心工作。一是积极与上级相关行业主管单位沟通协调,加强投标人交易行为监管,维护公共资源交易市场秩序。二是密切与纪检监察等有关职能部门的沟通联系,加强项目进场交易情况督查,加强对交易各环节监管,及时纠正交易过程中存在的问题,不断提升交易服务水平,努力实现阳光交易。

2024年某区公共资源交易中心上半年工作总结和下半年工作计划
一是强化服务理念,创新服务方式,深化作风建设,提高工作效能,进一步增强大局意识、责任意识和服务意识。坚持以优质服务、高效服务为工作标准,以熟练的业务技能、热情的服务态度、规范的服务行为、公正的办事作风和最大的社会效益,树立诚实守信的社会形象,打造优质高效的服务品牌。二是进一步落实交易项目的提前介入、主动服务工作机制,提前、主动与招标人联系,提供政策咨询、程序引导、业务指导等服务,帮助解决招标和采购中遇到的一些困难和问题。(三)坚持奋发进取,突出创新创优,不断创新公共资源交易中心工作。一是积极与上级相关行业主管单位沟通协调,加强投标人交易行为监管,维护公共资源交易市场秩序。二是密切与纪检监察等有关职能部门的沟通联系,加强项目进场交易情况督查,加强对交易各环节监管,及时纠正交易过程中存在的问题,不断提升交易服务水平,努力实现阳光交易。

人教版新课标小学数学二年级下册万以内的加法和减法(一)整理和复习说课稿
三、估算度的把握。《标准》在计算教学方面强调的内容之一是重视估算,培养估算意识。我们认为重视估算,就是对学生数感的培养,具体体现在能估计运算的结果,并对结果的合理性作出解释。本节课的设计就是让学生在具体情境中,学会两种估算方法,结合具体情况作出合理解释。四、教会学生单元整理与复习的方法,使学生终身受益。我们知道授人以渔而非鱼的道理。在本节课中,老师设计了引导学生学会整理与复习的方法,如:带着问题看书,将算式分类、归纳、总结出本单元所学内容,计算方法,注意地方,最后进行有针对性的练习。如果我们的老师从小就有意识地对学生进行学习方法的培养,学生将终身受益。我想我们教学研讨活动就是为了实现教育的最高境界:今天的教是为了明天的不教。

有理数教案
(一)旧知回顾(老师提出问题,同学回答。红色部分为学生回答后,老师给出的答案。)1、通过上节课的学习,你知道除了正数还有哪些数?答:1)0和负数。2)0既不是正数,也不是负数。2、用正数和负数表示具有相反意义的量。举例:如果把一个物体向后移动5m,记作移动-5m;那么这个物体向前移动5m,记作移动5m。原地不动,记作移动0m。

北师大版小学数学五年级下册《包装的学问》说课稿
将三盒磁带包成一包,共有几种方案?怎样包装才能节约包装纸?(接口处不计)这道题,我会组织每一位学生进行摆一摆、想一想、算出最优方案。此时,学生对于包装的问题已经有了从感性到理性的认识,因此,可以让学生将前面总结出来的规律进行完善,突出了教学重点。教师板书:重叠面积大的面,会节约包装纸。(四)综合实践,提高能力。在这一环节,我设计了一道题。如果把4盒磁带包装成一大盒。怎样包装才最节约包装纸?此题让学生小组合作动手摆一摆。学生汇报时,教师多媒体演示:学生根据前面总结出来的规律,会立刻回答出是第一种方案。此环节的设计,使学生在运用规律的基础上能够解决实际问题,得到最优方案,也突破了教学难点。(五)课堂总结。这一环节,我会让学生说一说自己的学习体会。然后送给学生两条名言。

初中化学人教版九年级上册《实验活动1氧气的实验室制取与性质》教案
【学习目标】1.知识与技能:知道氧气的制取及检验方法,复习巩固氧气的相关性质。2.过程与方法:通过“探究能使带火星木条复燃所需氧气的最低体积分数”的探究性学习,学习科学探究的基本方法。3.情感态度与价值观:提高实验设计的能力和合作意识,复习巩固相关的基本操作,培养学习化学的兴趣。【学习重点】氧气的实验室制取操作步骤和性质检验。【学习难点】实验操作过程中的注意事项。【课前准备】《精英新课堂》:预习学生用书的“早预习先起步”。《名师测控》:预习赠送的《提分宝典》。情景导入 生成问题1.复习引入:实验室用高锰酸钾制取氧气的反应原理是什么?操作步骤有哪些?2.明确学习目标,由学生对学习目标进行解读。合作探究 生成能力阅读课本P45~P46的内容。提出问题:实验室加热高锰酸钾制取氧气的实验中,使用了哪些仪器?哪部分是气体发生装置?哪部分是气体收集装置?为什么可用排水法收集气体?讨论交流:结合化学实验基本操作和氧气的性质讨论归纳。

北师大版初中数学九年级下册何时获得最大利润说课稿
(1)写出平均每天销售(y)箱与每箱售价x(元)之间的函数关系式.(注明范围)(2)求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数关系式(每箱的利润=售价-进价).(3)求出(2)中二次函数图象的顶点坐标,并求当x=40,70时W的值.在坐标系中画出函数图象的草图.(4)由函数图象可以看出,当牛奶售价为多少时,平均每天的利润最大?最大利润为多少?解:(1)当40≤x≤50时,则降价(50-x)元,则可多售出3(50-x),所以y=90+3(50-x)=-3x+240.当50<x≤70时,则升高(x-50)元,则可少售3(x-50)元,所以y=90-3(x-50)=-3x+240.因此,当40≤x≤70时,y=-3x+240.(2)当每箱售价为x元时,每箱利润为(x-40)元,平均每天的利润为W=(240-3x)(x-40)=-3x2+360x-9600.

北师大版初中数学九年级上册图形的放大与缩小说课稿
说教学难点:图形的放大与缩小的原理是“大小改变,形状不变“。针对小学生的年龄和认知特点,教材中“图形的放大与缩小”从对应边的比相等来进行安排,而对应角的不变也是形状不变必备的条件,是学生体会图形的相似所必需的。学生在学习的过程中很有可能会质疑到这一问题。(为什么直角三角形只需要同时把两条直角边放大与缩小?)所以我把“学生在观察、比较、思考和交流等活动中,感受图形放大、缩小,初步体会图形的相似。(对应边的比相等,对应角不变)”做为本节课的难点。说教法、学法:通过直观演示,情景激趣,结合生活让学生形成感性认识;引导学生经过观察、猜想、分析、操作、质疑、小组交流、合作学习、验证等过程形成理性认识。教学过程:(略)

北师大版初中数学九年级下册最大面积是多少说课稿
当然,在讨论的过程中,对个别学生要及时点拨利用相似三角形对应边的关系来求AD,至于S与x的关系式自然是水到渠成了。接着让同学们以小组为单位,派出代表展示自己的讨论成果。然后我进一步抛出重点问题3)这里S与x是一种什么函数关系?当x 取何值时,S的值最大?最大值是多少?这个例题和刚才的做一做非常相似。那么要求矩形的面积 就必须知道矩形的长和宽,通过学生的思考、讨论、大家都明白了S与x的关系一定是二次函数,要求面积的最大值,也就是求二次函数的最大值,这样就将实际问题转化为数学问题了.简单的小组交流过后,同学们争先恐后表达自己的观点:有的小组利用的是配方法,有的小组直接利用二次函数的顶点坐标求出了最大面积。 ,我及时的鼓励学生:大家真的很棒,老师为你们骄傲,请再接再厉。
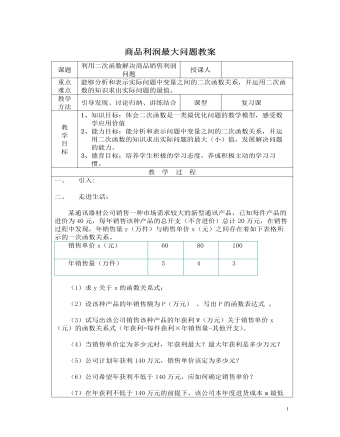
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值

在农产品(食品)深加工高成长企业产品推荐启动活动上的致辞讲话发言
在经济社会跨越发展的同时,这些年,x农业发展也呈现出乘风破浪、阔步前行的良好态势。2020年全省农业增加值增长x%,由全国第x位上升到第x位。我到x工作半年多,深刻感到x既是“美丽公园省”,也是“美食大观园”,真切感受到x农产品和特色食品等“x货”的独特魅力。可以说,“x货”是x自然风光、民族风情、特色风物的完美结晶和集大成者,今天集中推荐展示的x个单品、x个企业及x个公共品牌是“x货”的名优产品和优强品牌。

初三誓师大会学生发言讲话稿3分钟
三年前,我们怀着对未来的美好憧憬,带着家人与老师的殷殷期盼,兴奋地跨进了心仪已久的美丽的邗中校园。春来春去,杨柳依依,书写无悔年华;燕离燕归,白云点点,唱响人生奋斗的凯歌。微冷的春风淡去了烟尘与伤痛,沉淀在内心的,是缤纷的梦想和那收获前的耕耘与奋斗。蓦然回首,三年寒窗苦读,一千多个日日夜夜,铸就了我们必胜的信念与坚不可摧的意志。我们的目光,从来没有像今天这般坚定执着;我们的思想,从来没有像现在这般成熟饱满;我们的心灵,从来没有眼前这般激荡燃烧。






