-

(老师稿)国旗下讲话:庆祝“五一”国际劳动节
100多年前,世界上的劳动人民饱受资产阶级的剥削和压迫,工人每天工作的时间长达14到16个小时,尽管这样,他们还是经常不得温饱。1886年5月1日,在美国芝加哥,20万工人举行大罢工,要求实行8小时工作制。这一斗争得到世界各国人民的支持。 后来,国际工人组织为了纪念这个有意义的日子,就把这天定为国际劳动节。“五一”国际劳动节,是所有劳动人民的节日。在我国,各行各业的劳动者在自己平凡的岗位上辛勤劳动着,为我们创造了今天这样的幸福生活:时传祥伯伯是一名掏粪工人,它以主人翁的精神做好清洁工作,宁可一人脏,换来万人净,受到大家的尊敬;“铁人”王进喜不顾身体的虚弱,以“铁人”的精神奋斗在大庆油田几十年,为我国石油工业的发展建功立业;张秉贵,一个普普通通的售货员,几十年如一日,以自己胸中的“一团火”精神,为顾客热情报务,做出了不平凡的业绩;

(老师稿)国旗下讲话:以诚实守信为荣
一天,樵夫在河边砍树,不小心把斧子掉进了水里。可怜的樵夫瞪大双眼,想看清河底的情况,但河水太深了。“我可怎么办啊?” 樵夫喊道,“失去了斧子,我以后怎么养活孩子们?”他的话让龙王听见了。转瞬,龙王拿着一把斧子给樵夫看:“这是你的吗?”龙王问道。樵夫摇头道,说:“这不是。我的斧子是钢制的。”龙王再次潜入水中。一会儿,手里拿着一把斧子给樵夫看:“这是你的吧?”樵夫回答道:“这把也不是。”它是用金子做的,比我的要贵许多倍!”龙五把金斧子放到岸上,又一次潜入水中。这次浮出水面时,他拿的才是樵夫的斧子。“这个是我的!”樵夫兴奋地喊道。“那就好,另外两把现在也属于你了。它们是河水送给你的礼物,因为你刚才说了实话。”龙王笑着说。

(老师稿)国旗下讲话:如何冬季锻炼身体
同学们,这几天气温骤降,阵阵寒风袭来让我们感受到冬天已来到我们身边,同时我们也发现教室里感冒发烧的同学也多起来了,这都是我们的身体无法抵御寒冷结果。冬天可是个锻炼身体的好时候,我们可以积极参加体育锻炼,增强体质。一千多年前,在古希腊山岩上刻着这样一句格言:“如果你想聪明,跑步吧,如果你想强壮,跑步吧,如果你想健美,跑步吧。”这句格言向我们揭示了一个哲理——健壮体魄人人都可得到,那就得积极运动,坚持锻炼身体。同学们,相信你们每个人都有自己的理想,想当科学家,想当医生,军人,老师……可在实现这些理想的同时,得要有一个重要的前提,那就是你必须要有一个健康强壮的身体。如果你没有健全的身体,当了科学家也就谈不上创造与发明了,当了医生不但不能给病人看病,反而要人家来照顾你。所以,有一个健全的体魄对于我们的学习,长大为祖国建设有着很大的关系。我们应该从小做起,积极锻炼身体,为今后的工作、学习打下结实的基础。

(老师稿)国旗下讲话:如何面对挫折
在我们的成长过程中,既充满了成功的愉快,也会遇到各种各样的挫折。比如早上因起床晚,上学迟到而被老师批评;期末考试,尽管做了比较充分的准备可成绩却不理想;参加班干部竞选,自以为很有希望,结果却意外落选;课堂上没能回答出老师的提问;明明做了好事却被同学老师误会等等。这时,我们往往会产生焦虑、失望、忧虑、担心、痛苦等情绪反应。挫折是每个人都会遭遇的,我们不能绕它而行,无论是直面正视,还是迂回躲闪,都不能真正地摆脱它。因此,我们必须用积极的态度去面对挫折。下面,老师讲一个桑兰的故事,也许会给每一位同学以启示。桑兰,是我国一位著名的体操运动员,曾获得1995年全国城市运动会全能冠军,跳马冠军,自由体操亚军;1995年全国冠军赛跳马冠军;1996年全国锦标赛跳马亚军;1997年第八届全运会跳马冠军,全国锦标赛跳马亚军;1998年全国冠军赛跳马第二。 而然在第四届友好运动会体操赛场的一次赛前训练,一次偶然,桑兰的一个没有完成的手翻转体动作,头部着地,造成中枢神经严重损伤,双手和胸以下失去知觉。从她苏醒过来以后,她就没有流一滴眼泪;从她重新面对公众的目光那一刻起,她的面容就永远浮现着灿烂的微笑。

(母亲节)老师在国旗下的讲话:感恩父母
亲爱的少先队员们:你们知道吗,5月第二个星期日是什么节?(母亲节)6月第三个星期日又是什么节?(父亲节)那你知道为什么要有这两个节日吗?这是因为在人的一生中,对自己恩情最深的莫过于父母,是父母给予了我们生命,是父母辛勤地养育着我们,我们的成长凝结着父母的心血,每一个人都是在父母的悉心关怀、百般爱护和辛苦抚养下慢慢长大的。父母的亲子之爱只能用两个词语来形容——无私、伟大。他们可以为子女付出一切,也甘愿付出一切。所以说,父母之爱位于人世间各种各样的爱之上。但是我们有的队员很少知道父母的辛苦,总是伸手向父母要这要那,认为父母给孩子吃好、穿好、用好是天经地义的,在父母不满足他的要求时还耍脾气。要知道,感恩父母,孝敬父母是我们中华民族的传统美德。那么,今天的我们应该怎样孝敬父母呢?

国旗下讲话:爱红领巾,爱国旗(老师讲话)
各位老师,各位同学:大家早上好!刚才,我们都经历了一个庄严而神圣的时刻:伴随着初升的朝阳,五星红旗在雄壮嘹亮的国歌声中冉冉升起,猎猎飘扬。是的,这就是我们的国旗,象征着浴血奋战中的力量和勇气,象征着外交活动时的形象与尊严,象征着和平年代的理智与激情。每一次五星红旗的升起,都会在中国人的心灵深处升腾起一股热浪,这是一份自豪和中国人的尊严,是一股油然而生充满力量的爱国情怀。当奥运会领奖台上的五星红旗伴随着国歌声一次次升起的时候,全世界的炎黄子孙都为之欢呼雀跃;当登山健儿把五星红旗插上世界顶峰——珠穆朗玛峰时,全世界的华人都为之骄傲;当嵌着五星红旗的人造卫星和“神舟”号宇宙飞船升入太空的时候,中国让世界各国刮目相看;当中国综合国力日渐强大的时候,全世界把目光投向了中国——站在国旗下,我为祖国骄傲。这份炽热燃烧、薪火相传的民族情怀是庄严和神圣的,却也是平凡和普通的。我们每周一次的升旗仪式上,在雄壮的国歌声中,队员们都庄严的敬着少先队队礼,神情专注,这也无疑是一种爱国的表现。曾经,抛头颅、洒热血是烈士们表达对祖国热爱的方式。而生活在今天和平年代的我们如何表达对祖国的热爱呢?那就是先从佩戴好红领巾开始。

国旗下的讲话:珍惜自己(老师讲话)
国旗下的讲话:珍惜自己(老师讲话)同学们:早上好!今天集体晨会的题目是:珍惜自己。老师先给大家讲个故事吧!一个生长在孤儿院中的小男孩,常常悲观地问院长:“像我这样的没人要的孩子,活着究竟有什么意思?”院长总是笑而不答。一天,院长交给孩子一块石头,让他拿到市场上去卖,但无论别人出多少钱,绝对不能卖。第二天,孩子惊奇地发现,不少人好奇地对他的石头感兴趣,且价钱越出越高。第三天,在黄金市场上,石头的价钱高了10倍。最后,当石头被拿到宝石市场上时,石头的身价又涨了10倍,更由于男孩怎么都不卖,竟被传扬为“稀世珍宝”。后来,院长是这样说的:“生命的价值就像这块石头一样,在不同的环境下就会有不同的意义。一块不起眼的石头,由于你的珍惜而提升了它的价值,竟被传为稀世珍宝。你不就像这块石头一样?只要自己看重自己,自我珍惜,生命就有意义,有价值”。

人教A版高中数学必修二简单随机抽样教学设计
知识探究(一):普查与抽查像人口普查这样,对每一个调查调查对象都进行调查的方法,称为全面调查(又称普查)。 在一个调查中,我们把调查对象的全体称为总体,组成总体的每一个调查对象称为个体。为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,每一个调查对象的相应指标作为个体。问题二:除了普查,还有其他的调查方法吗?由于人口普查需要花费巨大的财力、物力,因而不宜经常进行。为了及时掌握全国人口变动状况,我国每年还会进行一次人口变动情况的调查,根据抽取的居民情况来推断总体的人口变动情况。像这样,根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和判断的方法,称为抽样调查(或称抽查)。我们把从总体中抽取的那部分个体称为样本,样本中包含的个体数称为样本量。

精编中学教师个人顶岗实习心得体会与感受八篇
在萃文中学实习已经两个多月了,从第一周的听课到现在上课的收放自如,说没有付出努力是不可能的。但现在一步步走来,看到这群初一的孩子们越来越听话,上课时越来越认真,作业交的越来越及时,心里就像有朵花悄然开放,感觉每节课都是美滋滋的。但是总有这么一个孩子觉得中考不考生物,在我的课上一开始调皮捣蛋的,后来我跟他谈过几次心,他说对于我是没有意见的,知识单纯的不喜欢生物这个学科,于是我跟他定下协议,认认真真的听我几节课,我会让他知道就算中考不考,学些生物知识在生活中引物很有用。以这个学生为起点,我设计了“我们都是大医生”这节课,让学生们感受到生活中处处是科学。
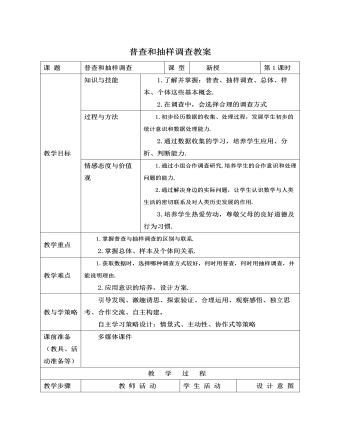
北师大初中七年级数学上册普查和抽样调查教案2
1.举例说明什么时候用普查的方式获得数据较好,什么时候用抽样调查的方式获得数据较好?2、下列调查中分别采用了那些调查方式?⑴为了了解你们班同学的身高,对全班同学进行调查.⑵为了了解你们学校学生对新教材的喜好情况,对所有学号是5的倍数的同学进行调查。3、说明在以下问题中,总体、个体、样本各指什么?⑴为了考察一个学校的学生参加课外体育活动的情况,调查了其中20名学生每天参加课外体育活动的时间.⑵为了了解一批电池的寿命,从中抽取10只进行实验。⑶为了考察某公园一年中每天进园的人数,在其中的30天里对进园的人数进行了统计。通过本节课的学习,同学们有什么收获和疑问?1、基本概念:⑴.调查、普查、抽样调查.⑵.总体、个体、样本.2、何时采用普查、何时采用抽样调查,各有什么优缺点?

北师大初中数学九年级上册复杂图形的三视图2教案
教学目标:1.会画直棱柱(仅限于直三棱柱和直四棱柱)的三种视图,体会这几种几何体与其视图之间的相互转化。2. 会根据三视图描述原几何体。教学重点:掌握直棱柱的三视图的画法。能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法一、实物观察、空间想像观察:请同学们拿出事先准备好的直三棱柱、直四棱柱,根据你所摆放的位置经过 想像,再抽象出这两个直棱柱的主视图,左视图和俯视图。绘制:请你将抽象出来的三种视图画出来,并与同伴交流。比较:小亮画出了其中一个几何体的主视图、左视图和俯视图,你认为他画的对不对?谈谈你的看法。拓展:当你手中的两个直棱柱摆放的角度变化时,它们的三种视图是否会随之改变?试一试。
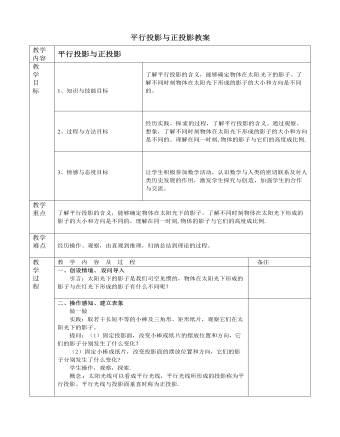
北师大初中数学九年级上册平行投影与正投影2教案
四、范例学习、理解领会例2 某校墙边有甲、乙两根木杆。已知乙木杆的高度为1.5m.(1)某一时刻甲木杆在阳光下的影子如图5-6所示,你能画出此时乙木杆的影子吗?(用线段表示影子)(2)在图中,当乙木杆移动到什么位置时,其影子刚好不落在墙上?(3)在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗?学生画图、 实验、观察、探索。五、随堂练习课本随堂练习 学生观察、画图、合作交流。六、课堂总结本节课通过各种实践活动,促进大家对内容的理解,本课内容,要体会物体在太阳光下形成的不同影子,在操作中观察不 同时刻影子的方向和大小变化特征。在同一时刻,物体的影子与它们的高度成比 例.

北师大初中数学九年级上册一元二次方程的解及其估算2教案
探索1:上节我们列出了与地毯的花边宽度有关的方程。地毯花边的宽x(m),满足方程 (8―2x)(5―2x)=18也就是:2x2―13x+11=0你能估算出地毯花边的宽度x吗?(1)x可能小于0吗?说说你的理由;_____________________________.(2)x可能大于4吗?可能大于2.5吗?为什么?(3)完成下表x 0 0.5 1 1.5 2 2.52x2-13x+11 (4)你知道地毯花边的宽x(m)是多少吗?还有其他求解方法吗?与同伴交流。探索2:梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,也就是x2+12x―15=0(1)你能猜出滑动距离x(m)的大致范围吗?(2)x的整数部分是_____?十分位是_______?x 0 x2+12x-15 所以 ___<x<___进一步计算x x2+12x-15 所以 ___<x<___因此x 的整数部分是___,十分位是___.三、当堂训练:完成课本34页随堂练习四、学习体会:五、课后作业

北师大初中数学九年级上册一元二次方程2教案
三、课堂检测:(一)、判断题(是一无二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)1. 5x2+1=0 ( ) 2. 3x2+ +1=0 ( )3. 4x2=ax(其中a为常数) ( ) 4.2x2+3x=0 ( )5. =2x ( ) 6. =2x ( ) (二)、填空题.1.方程5(x2- x+1)=-3 x+2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.2.如果方程ax2+5=(x+2)(x-1)是关于x的一元二次方程,则a__________.3.关于x的方程(m-4)x2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程。四、学习体会:五、课后作业
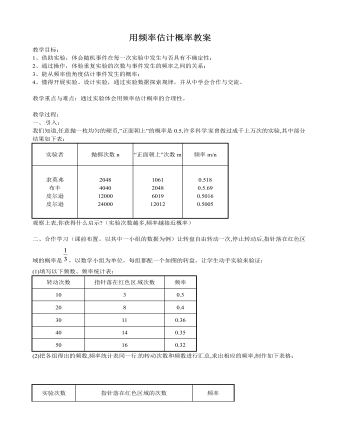
北师大初中数学九年级上册用频率估计概率2教案
(4)议一议:频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何?结论:从上面的试验可以看到:当重复实验的次数大量增加时,事件发 生的频率就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率。三、做一做:1.某运动员投篮5次, 投中4次,能否说该运动员投一次篮,投中的概率为4/5?为什么?2.回答下列问题:(1)抽检1000件衬衣,其中不合格的衬衣有2件,由 此估计抽1件衬衣合格的概率是多少?(2)1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少?
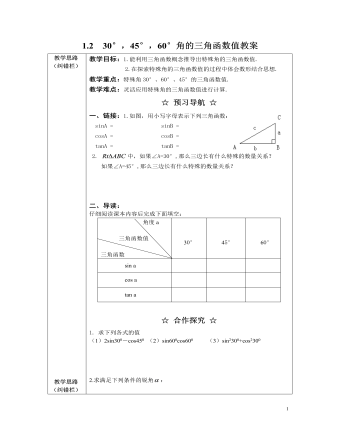
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中数学九年级上册正方形的性质1教案
在Rt△ABC中,AC=AB2+BC2=12+12=2(cm),∴FC=AC-AF=2-1(cm),∴BE=2-1(cm).方法总结:正方形被对角线分成4个等腰直角三角形,因此在正方形中解决问题时常用到等腰三角形的性质与直角三角形的性质.【类型三】 利用正方形的性质证明线段相等如图,已知过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.解析:由PE⊥BC,PF⊥CD知四边形PECF为矩形,故有EF=PC,这时只需说明AP=CP,由正方形对角线互相垂直平分可知AP=CP.证明:连接AC,PC,如图.∵四边形ABCD为正方形,∴BD垂直平分AC,∴AP=CP.∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴PC=EF,∴AP=EF.方法总结:(1)在正方形中,常利用对角线互相垂直平分证明线段相等;(2)无论是正方形还是矩形,经常连接对角线,这样可以使分散的条件集中.

北师大初中九年级数学下册二次函数与一元二次方程2教案
教学目标:1.知道二次函数与一元二次方程的联系,提高综合解决问题的能力.2.会求抛物线与坐标轴交点坐标,会结合函数图象求方程的根.教学重点:二次函数与一元二次方程的联系.预设难点:用二次函数与一元二次方程的关系综合解题.☆ 预习导航 ☆一、链接:1.画一次函数y=2x-3的图象并回答下列问题(1)求直线y=2x-3与x轴的交点坐标; (2)解方程2x-3=0(3)说出直线y=2x-3与x轴交点的横坐标和方程根的关系2.不解方程3x2-2x+4=0,此方程有 个根。二、导读画二次函数y= x2-5x+4的图象1.观察图象,抛物线与x轴的交点坐标是什么?2.求一元二次方程x2-5x+4=0的解。3.抛物线与x轴交点的横坐标与一元二次方程x2-5x+4=0的解有什么关系?(3)一元二次方程ax2+bx+c=0是二次函数y=ax2+bx+c当函数值y=0时的特殊情况.二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?

北师大初中七年级数学上册多边形和圆的初步认识教案2
1、 如图4-25,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流2、 画一个半径是2cm的圆,并在其中画一个圆心为60º的扇形,你会计算这个扇形的面积吗?与同伴交流。教师对答案进行汇总,讲解本题解题思路:1、 因为一个圆被分成了大小相同的扇形,所以每个扇形的圆心角相同,又因为圆周角是360º,所以每个扇形的圆心角是360º÷3=120º,每个扇形的面积为整个圆的面积的三分之一。2、 先求出这个圆的面积S=πR²=4π,60÷360=1/6扇形面积=4π×1/6=2π/3【设计意图】运用小组合作交流的方式,既培养了学生的合作意识和能力,又达到了互帮互助以弱带强的目的,使学习比较吃力的同学也能参与到学习中来,体现了学生是学习的主体。

北师大初中七年级数学上册比较线段的长短教案1
1.了解“两点之间,线段最短”.2.能借助尺、规等工具比较两条线段的大小,能用圆规作一条线段等于已知线段.3.了解线段的中点及线段的和、差、倍、分的意义,并能根据条件求出线段的长.一、情境导入爱护花草树木是我们每个人都应具备的优秀品质.从教学楼到图书馆,总有少数同学不走人行道而横穿草坪(如图),同学们,你觉得这样做对吗?为了解释这种现象,学习了下面的知识,你就会知道.二、合作探究探究点一:线段长度的计算【类型一】 根据线段的中点求线段的长如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.(1)求线段MN的长;(2)根据(1)中的计算过程和结果,设AB=a,其它条件不变,你能猜出MN的长度吗?请用简洁的话表达你发现的规律.