-

人教部编版七年级语文上册如何突出中心教案
我们一家乘车行驶在黄土高原上,眺望远处云朵,尽情享受着清风的洗礼……因为我们要回老家喽!倘若乖乖地欣赏美景,是坐不住的。虽说有起伏不定的高原,波涛汹涌的黄河,不时从石缝里“蹦”出来的水丝帘,一望澄澈的蓝天,悠然飘过的白云……可当这一切的美景同时“刷”在你的眼前,且接连不断地出现时,还是会让你感到几分乏味。因为,这可是八小时的长途跋涉啊!每到这时候,车里的人们就疯狂了起来。虽说只有区区四人,可还是组成了一个超级合唱团。不信你看爸爸已经兴奋起来。只见他清清嗓子,扭动身子,接着便“肆无忌惮”地高声唱起来。妈妈则是一副欲唱又止的样子,最终也只是淡淡地笑了笑。在这一刹那,妈妈神情是最复杂也是最可爱的。是快乐还是骄傲?是幸福还是羞涩?总之,略有些放不开。后来,她也开始有节奏地在车门上敲击,敲出一串美妙又兴奋的声音。好像她所有的快乐都被谱成了一首无拘无束的歌。

人教部编版七年级语文上册学会记事教案
家是圆心,我们都是圆内的点,爸爸、妈妈和我,我们围着圆心在走,走出一个圆满的家。(开篇点题。)清风摇曳梧桐树的小时候——(独立成段,设置场景,富有意境。)月亮又悄悄爬上了窗外的梧桐树,我靠在床头,该是听妈妈讲故事的时候了,可是妈妈又晚督班去了。妈妈是一名老师,每天兢兢业业,总有忙不完的事情。每次回家,总是带着匆匆的脚步,充斥着紧张的氛围,有时怀里还抱着几本厚厚的书。“妈妈,你不爱我了吗?为什么不在我身边?”我握住妈妈的手,她的手上还有白色的粉笔灰。“孩子……”妈妈哽住了,转过头去,眼里含着透明的水珠。她摸了摸我的头,指了指窗外的月亮:“月儿圆的时候,妈妈就会回来。”我蹦蹦跳跳跑到窗前,每个夜晚不停地寻找那圆圆的月亮——那是妈妈回来的希望。在梧桐摇曳,月儿圆圆缺缺的岁月里,充满了等待的苦涩、团聚的欢乐。

人教部编版语文八年级上册白杨礼赞教案
【设计意图】帮助学生理解象征手法,明确本体与象征体的联系,体会作者的情感。通过朗读加深学生对重点句子的理解,让这种精神内化为个人力量。三、练习象征手法的运用请同学们说一说这些形象可以象征什么?课件出示:落叶、荷花、蜡烛、梅花、翠竹、鹰、太阳、孔雀、牛生答:蜡烛燃烧自己照亮别人,可以象征舍己为人的品质,可以象征教师。……师:大家的思路逐渐被打开了,请同学们拿出纸和笔开始写作。注意:本文前半部分是对白杨树的自身形象进行描绘,再通过联想和想象赋予它一定的象征意义,所以同学们不要一开始就写什么物象征什么。结束语:同学们,一篇优秀的散文,就如一幅无形的画,又恰似一首读不尽的诗,茅盾先生的散文达到了如诗如画的艺术境界,白杨树在特定的历史时期被赋予了特定的内涵。让我们再次以茅盾先生写的小诗《题白杨图》作结,向白杨树的精神致敬,向中华儿女身上的正直、质朴、紧密团结、力求上进、坚强不屈的精神和意志致敬!(师生同读教材P81《题白杨图》一诗)

人教部编版语文八年级上册背影教案
一提到朱自清,大家脑海里闪现出的便是《荷塘月色》《背影》《匆匆》等美文。位于昆明司家营的朱自清旧居,这座“一颗印”老宅不仅承载着七十多年前以朱自清为代表的清华文科研究所师生的家国情怀,也记录着朱自清那些不为人知的故事。这些故事,将撕开朱自清身上“散文家”“诗人”“学者”“民主战士”的标签,让大家看到一个不一样的朱自清!“时尚达人”朱自清1942年冬天,昆明天气格外寒冷,如何温暖过冬成了朱自清头疼的大问题。身上的旧皮袍已经缝补了许多次,早已抵挡不住瑟瑟寒风。掏掏口袋,发现生活费都够呛,更不要说缝制新棉袍,于是朱自清做了一个决定。趁着龙头街赶街的日子,朱自清给自己挑了一件赶马人穿的、制作粗糙、价格便宜的毡披风。朱自清一毡多用,出门时,他就将毡披风披在身上御寒,晚上睡觉时,毡披风一脱就当被褥。朱自清上街,里边穿西装,外边穿赶马人的毡披风,给联大师生留下了深刻的印象。这件毡披风由于太过显眼,被誉为“联大三绝”,也成了他教授生活清贫的标志,以至于后来多次出现在回忆朱自清的朋友的笔下。

人教部编版语文八年级上册三峡教案
此外,多种形式的朗读,为学生在朗读中理解字词、内容、情感打下了基础。素养提升《三峡》中的修辞手法1.并提为了使句子紧凑、文笔简练,古人常用并提法行文,把本来应该写成两个短语或两个句子的话,合并为形式上的一个短语或一个句子,把相同的语句成分放在一起并提,但表意上仍然必须按照两个短语或句子的组合关系来分别相承,这种修辞手法就叫并提。这种句子翻译时应分为两句。如:(1)“自非亭午夜分,不见曦月。”“亭午”“夜分”是两个不并存的时间,“曦”和“月”是两种不同的自然现象,合起来是讲不通的,这句话应理解为“自非亭午,不见曦;自非夜分,不见月”(如果不是在正午,就看不到太阳;如果不是在半夜,就看不到月亮)。(2)“素湍绿潭,回清倒影。”这句和上句一样,应理解为“素湍回清,绿潭倒影”(白色的急流中有回旋的清波,绿色的潭水中有倒映着的各种景物的影子)。

人教部编版语文八年级上册愚公移山教案
阴阳原是指日光的向背,向日为阳,背日为阴。我国古代地名中的“阴”和“阳”实际上是一种方位指示,“日之所照曰阳”,也就是说太阳所能照到的地方就称为阳。 山水阴阳是说古代以山南、水北为阳,以山北、水南为阴。 形成这种局面的原因是山峰高耸,日光能照射到的地方是山的南面;而河流位于地平面以下,所以太阳能照射到的地方其实是河流的北面。 故有“山南水北谓之阳,山北水南谓之阴”的说法。在我国历史上,很多地名及地理表述都与此关系密切,如江阴、衡阳、汉阳等。 《愚公移山》 中说:“指通豫南,达于汉阴。” 其中的“汉阴”是指汉水的南岸。 “泰山之阳,汶水西流;其阴,济水东流”(姚鼐《登泰山记》)、“所谓华山洞(南宋王象之《舆地纪胜》写为‘华阳洞’。 看正文下句,应为‘华阳洞’)者,以其乃华山之阳名之也”

人教部编版语文八年级上册与朱元思书教案
吴均是一位善写山水的大家,他自小好学而又才智出众,但“家世寒贱”,性格耿直。在门阀制度相当严格的南朝梁,出身于庶族寒门的人,想要在政治上得到重用,着实不易,再加上他性格直来直去,口无遮拦,更是会四处碰壁。所幸的是,起先著名文史学家沈约看中了吴均的文章,“颇相称赏”。接着,吴均得到了刺史柳恽的赏识,提拔他当了郡主簿,常在一起赋诗答对。他的诗文“清拔有古气”,自成一家,时人纷纷效仿,称为“吴均体”。书信内容为何是山水游记魏晋六朝是中国历史上政治最混乱、社会最痛苦的时代,然而却是精神上极自由、极富智慧和艺术精神的时代。大自然成了情趣高雅之士审美活动的重要背景和舞台,移情山水成了当时的社会风尚。在书信中描画山水,寄托情志,成为好友间交流的一种流行方式,文人们通过书信内敛地表露自己的人生取向,他们的文学经历给后世留下了宝贵的文化遗产。吴均的《与朱元思书》《与施从事书》和《与顾章书》,以及陶弘景的《答谢中书书》皆是如此。

人教部编版七年级语文上册女娲造人教案
【设计亮点】这是一篇自读课文,依据统编教材“教读—自读—课外阅读”的“三位一体”的阅读教学体系的特点和单元整体教学要求,我将本课设计为自读指导课型。我以学生自我阅读实践为主线,设计了四个循序渐进的学生阅读实践活动:初读,激发学生的阅读兴趣,了解学生的阅读认知水平;速读,落实单元能力目标,初步体会神话大胆的想象以及离奇而又合情合理的情节,初步感知女娲的形象;美读,深入品悟女娲形象,进一步体会课文想象奇特而又合情合理的特点;联读,激活学生思维,引导学生深入开展阅读实践活动,深入理解课文中丰富的想象是根植于现实的,而且是合情合理的。通过“四步”阅读,引导学生逐步自求自得,使教读课所学知识、方法和能力得到有效的迁移和拓展。最后,通过布置作业板块将阅读引向课外,实现课内外的有机勾连。【资料链接】袁珂和《中国古代神话》

人教部编版七年级语文上册植树的牧羊人教案
【设计意图】结合资料,多角度、多层次地探讨文章的主题,拓展学生对文章主题认识的深度。四、联系自身,畅谈感悟启示师:牧羊人的精神启迪了世人,也启迪着我们,如何在现实生活中学习他的精神?如何对待自己的人生,创造自己的人生奇迹呢?请结合自己的生活体验,谈谈你从中得到的启示。预设(1)牧羊人几十年只重复做一件事——植树,但是他改变了人们的生存环境,更改变了世界,他代表了那些为改变人类命运而不断奋斗的人,我们就应该做这样的人,做对社会有益的事。不管事情多么地简单,把它做到极致,持续不断地努力去做,就一定可以为人类做出贡献,创造奇迹!(2)牧羊人虽然是一个普通人,但他心怀大爱,几十年默默无闻、不计回报地植树,给众人创造了幸福。启发我即使是最普通的人,也有能力创造,只要我们心怀大爱,就能创造幸福,给予他人幸福。不必去求回报,因为创造就体现出人生的价值。

北师大初中数学九年级上册一元二次方程的解及其估算2教案
探索1:上节我们列出了与地毯的花边宽度有关的方程。地毯花边的宽x(m),满足方程 (8―2x)(5―2x)=18也就是:2x2―13x+11=0你能估算出地毯花边的宽度x吗?(1)x可能小于0吗?说说你的理由;_____________________________.(2)x可能大于4吗?可能大于2.5吗?为什么?(3)完成下表x 0 0.5 1 1.5 2 2.52x2-13x+11 (4)你知道地毯花边的宽x(m)是多少吗?还有其他求解方法吗?与同伴交流。探索2:梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,也就是x2+12x―15=0(1)你能猜出滑动距离x(m)的大致范围吗?(2)x的整数部分是_____?十分位是_______?x 0 x2+12x-15 所以 ___<x<___进一步计算x x2+12x-15 所以 ___<x<___因此x 的整数部分是___,十分位是___.三、当堂训练:完成课本34页随堂练习四、学习体会:五、课后作业
北师大初中数学九年级上册概率与游戏的综合运用2教案
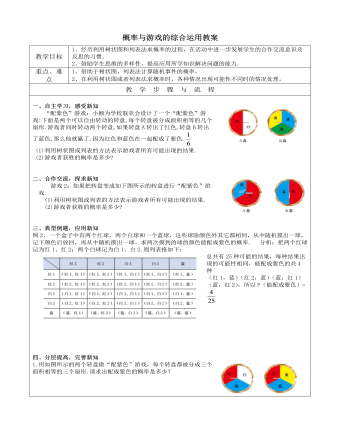
三、典型例题,应用新知例2、一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率. 分析:把两个红球记为红1、红2;两个白球记为白1、白2.则列表格如下:总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),所以P(能配成紫色)= 四、分层提高,完善新知1.用如图所示的两个转盘做“配紫色”游戏,每个转盘都被分成三个面积相等的三个扇形.请求出配成紫色的概率是多少?2.设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为 五、课堂小结,回顾新知1. 利用树状图和列表法求概率时应注意什么?2. 你还有哪些收获和疑惑?

北师大初中数学九年级上册简单图形的三视图2教案
教学目标:1.经历由实物抽象出几何体的过程,进一步发展空间观念。2.会画圆柱、圆锥、球的三视图,体会这几种几何体与其视图之间的相互转化。3.会根据三视图描述原几何体。教学重点:掌握部分几何体的三视图的画法,能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法教学过程设计一、实物观察、空间想像设置:学生利用准备好的大小相同的正方形方块,搭建一个立体图形,让同学们画出三视图。而后,再要求学生利用手中12块正方形的方块实物,搭建2个立体图形,并画出它们的三视图。学生分小组合作交流、观察、作图。议一议1.图5-14中物体的形状分别可以看成什么样的几何体?从正面、侧面、上面看这些几何体,它们的形状各是什么样的?2.在图5-15中找出图5-14中各物体的主视图。3.图5-14中各物体的左视图是什么?俯视图呢?

北师大初中数学九年级上册利用相似三角形测高2教案
[想一想]同学们经历了上述三种方法,你还能想出哪些测量旗杆高度的方法?你认为最优化的方法是哪种?思路点拔:1、如果旗杆周围有足够地空地使旗杆在太阳光照射下影子都在平地上,并能测出影子的长度,那么,可以在平地垂直树一根小棒,等到小棒的影子恰好等于棒高时,再量旗杆的影子,此时旗杆的影子长度就是这个旗杆的高度.2、可以采用立一个已知长度的参照物在旗杆旁照相后量出照片中旗杆与参照物的长度根据线段成比例来进行计算.3、拿一根知道长度的直棒,手臂伸直,不断调整自己的位置,使直棒刚好完全挡住旗杆,量出此时人到旗杆的距离、人手臂的长度和棒长,就可以利用三角形相似来进行计算.等等.第四环节 课堂小结1、本节课你学到了哪些知识?2、在运用科学知识进行实践过程中,你是否想到最优的方法?3、在与同伴合作交流中,你对自己的表现满意吗?第五环节 布置作业,反思提炼

北师大初中数学九年级上册复杂图形的三视图2教案
教学目标:1.会画直棱柱(仅限于直三棱柱和直四棱柱)的三种视图,体会这几种几何体与其视图之间的相互转化。2. 会根据三视图描述原几何体。教学重点:掌握直棱柱的三视图的画法。能根据三视图描述原几何体。教学难点:几何体与视图之间的相互转化。培养空间想像观念。课型:新授课教学方法:观察实践法一、实物观察、空间想像观察:请同学们拿出事先准备好的直三棱柱、直四棱柱,根据你所摆放的位置经过 想像,再抽象出这两个直棱柱的主视图,左视图和俯视图。绘制:请你将抽象出来的三种视图画出来,并与同伴交流。比较:小亮画出了其中一个几何体的主视图、左视图和俯视图,你认为他画的对不对?谈谈你的看法。拓展:当你手中的两个直棱柱摆放的角度变化时,它们的三种视图是否会随之改变?试一试。
北师大初中数学九年级上册平行投影与正投影2教案
四、范例学习、理解领会例2 某校墙边有甲、乙两根木杆。已知乙木杆的高度为1.5m.(1)某一时刻甲木杆在阳光下的影子如图5-6所示,你能画出此时乙木杆的影子吗?(用线段表示影子)(2)在图中,当乙木杆移动到什么位置时,其影子刚好不落在墙上?(3)在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗?学生画图、 实验、观察、探索。五、随堂练习课本随堂练习 学生观察、画图、合作交流。六、课堂总结本节课通过各种实践活动,促进大家对内容的理解,本课内容,要体会物体在太阳光下形成的不同影子,在操作中观察不 同时刻影子的方向和大小变化特征。在同一时刻,物体的影子与它们的高度成比 例.

北师大初中数学九年级上册一元二次方程2教案
三、课堂检测:(一)、判断题(是一无二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)1. 5x2+1=0 ( ) 2. 3x2+ +1=0 ( )3. 4x2=ax(其中a为常数) ( ) 4.2x2+3x=0 ( )5. =2x ( ) 6. =2x ( ) (二)、填空题.1.方程5(x2- x+1)=-3 x+2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.2.如果方程ax2+5=(x+2)(x-1)是关于x的一元二次方程,则a__________.3.关于x的方程(m-4)x2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程。四、学习体会:五、课后作业
北师大初中数学九年级上册用频率估计概率2教案
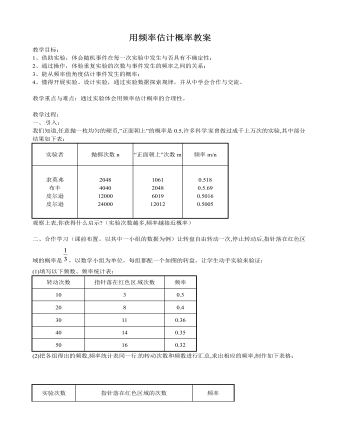
(4)议一议:频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何?结论:从上面的试验可以看到:当重复实验的次数大量增加时,事件发 生的频率就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率。三、做一做:1.某运动员投篮5次, 投中4次,能否说该运动员投一次篮,投中的概率为4/5?为什么?2.回答下列问题:(1)抽检1000件衬衣,其中不合格的衬衣有2件,由 此估计抽1件衬衣合格的概率是多少?(2)1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少?

北师大初中数学九年级上册反比例函数的图象2教案
观察 和 的图象,它们有什么相同点和不同点?学生小组讨论,弄清上述两个图象的异同点。交流讨论反比 例函数图象是中心对称图形吗?如果是,请找出对称中心.反比例函数图象是轴对称图形吗?如果是,请指出它的对称轴.二、随堂练习课本随堂练习 [探索与交流]对于函数 , 两支曲线分别位于哪个象限内?对于函数 ,两支曲线又分别位于哪个象限内?怎样区别这两个函数的图象。学生分四人小组全班探索。 三、课堂总结在进行函数的列表,描点作图的活动中,就已经渗透了反比例函数图象的特征,因此在作图象的过程中,大家要进行积极的探索 。另外,(1)反比例函数的图象是非线性的,它的图象是双曲线;(2)反比例 函数y= 的图像,当k>0时,它的图像位于一、三象限内,当k<0时,它的图像位于二、四象限内;(3)反比例函数既是中心对称图形,又是轴对称图形。

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册利用两角判定三角形相似2教案
合探2 与同伴合作,两个人分别画△ABC和△A′B′ C′,使得∠A和∠A′都等于∠α,∠B和∠B′都等于∠β,此时,∠C与∠C′相等吗?三边的比 相等吗?这样的两个三角形相似吗?改变∠α,∠β的大小,再试一试.四、导入定理判定 定理1:两角分别相等的两个三角形相似.这个定理的 出 现为判定两三角形相似增加了一条新的途径.例:如图,D ,E分别是△ABC的边AB,AC上的点,DE∥BC,AB= 7,AD=5,DE=10,求B C的长。解:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC(两角分别相等的两 个三角形相似).∴ ADAB=DEBC.∴BC=AB×DEAD = 7×105=14.五、学生练习:1. 讨论随堂练 习第1题有一个锐角相等的两个直角三角形是否相似?为什么?2.自己独立完成随堂练习第2题六、小结本节主要学习了相似三角形的定义及相似三角形的判定定理1,一定要掌握好这个定理.七、作业:








