-

部编版语文八年级下册《写作:学写故事》教案
【目标导航】1.通过多个故事的学习,能够选择有波折的典型材料,并学会画故事情节图;2.交流阅读故事的心得体会,掌握创写故事的基础知识,激发学生的联想与想象,并合理的运用到写作中;3.通过多个故事的训练,培养写作兴趣,能够多问“为什么”“怎么样”,写出比较精彩的故事。在创编故事中学会尊重他人的爱,学会关爱他人。一、以小组为单位,围绕一个话题,同学自由发挥想象,开展故事接龙活动。二、在你的身边或社会上,每天都在发生着各种各样有趣的或有意义的事。以某一件事为素材,展开合理的想象,自拟题目,写一篇故事。不少于600字。三、我们熟悉的各种事物,都可能引发故事,比如眼睛、头发、嘴巴,比如书包、校服、手机,又比如军训、旅游、社会实践活动,等等。这些物或事一定有不少值得挖掘的地方,有不少出人意外的富有戏剧性的故事。以《 的故事》为题,写一篇作文。不少于600字。

部编版语文八年级下册《写作:学写游记》教案
【目标导航】1.培养留心观察、勤于考证的意识,能初步认识到“行万里路”是增长人生见识和锻炼独立生活能力的必要途径。2.抓住特点描写景物,重点突出,详略得当。3.在写作活动中了解祖国大好河山,增强热爱家乡和祖国的情感,学写文情并茂的游记。【课时安排】2课时。【课时分配】建议第一课时进行作文指导与写作,第二课时进行批改、评讲、修改。了解作文文题,熟悉作文要求,搜集相关素材,为习作做准备。1.游记常常要对某处景物做定点观察,以写出景物的特点。选择你游览过的一个景点,围绕其中的一处风景,写一个片段。200字左右。2.我们应该都有过出游的经历。旅途中,我们不仅观赏自然风光,了解民风民俗,同时也会有许多新奇的感受,产生很多思考和遐想。自拟题目,写一篇游记。不少于600字。3.你一定看过一些展览,参观过一些纪念馆或博物馆,请选择一次这样的经历,以《参观 》为题,写一篇参观记。不少于600字。

北师大初中九年级数学下册二次函数与一元二次方程1教案
解:(1)设第一次落地时,抛物线的表达式为y=a(x-6)2+4,由已知:当x=0时,y=1,即1=36a+4,所以a=-112.所以函数表达式为y=-112(x-6)2+4或y=-112x2+x+1;(2)令y=0,则-112(x-6)2+4=0,所以(x-6)2=48,所以x1=43+6≈13,x2=-43+6<0(舍去).所以足球第一次落地距守门员约13米;(3)如图,第二次足球弹出后的距离为CD,根据题意:CD=EF(即相当于将抛物线AEMFC向下平移了2个单位).所以2=-112(x-6)2+4,解得x1=6-26,x2=6+26,所以CD=|x1-x2|=46≈10.所以BD=13-6+10=17(米).方法总结:解决此类问题的关键是先进行数学建模,将实际问题中的条件转化为数学问题中的条件.常有两个步骤:(1)根据题意得出二次函数的关系式,将实际问题转化为纯数学问题;(2)应用有关函数的性质作答.

北师大初中九年级数学下册二次函数与一元二次方程2教案
教学目标:1.知道二次函数与一元二次方程的联系,提高综合解决问题的能力.2.会求抛物线与坐标轴交点坐标,会结合函数图象求方程的根.教学重点:二次函数与一元二次方程的联系.预设难点:用二次函数与一元二次方程的关系综合解题.☆ 预习导航 ☆一、链接:1.画一次函数y=2x-3的图象并回答下列问题(1)求直线y=2x-3与x轴的交点坐标; (2)解方程2x-3=0(3)说出直线y=2x-3与x轴交点的横坐标和方程根的关系2.不解方程3x2-2x+4=0,此方程有 个根。二、导读画二次函数y= x2-5x+4的图象1.观察图象,抛物线与x轴的交点坐标是什么?2.求一元二次方程x2-5x+4=0的解。3.抛物线与x轴交点的横坐标与一元二次方程x2-5x+4=0的解有什么关系?(3)一元二次方程ax2+bx+c=0是二次函数y=ax2+bx+c当函数值y=0时的特殊情况.二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
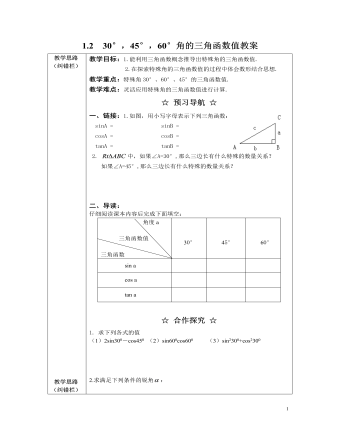
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示

北师大初中九年级数学下册切线的判定及三角形的内切圆教案
解析:(1)连接BI,根据I是△ABC的内心,得出∠1=∠2,∠3=∠4,再根据∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,得出∠BIE=∠IBE,即可证出IE=BE;(2)由三角形的内心,得到角平分线,根据等腰三角形的性质得到边相等,由等量代换得到四条边都相等,推出四边形是菱形.解:(1)BE=IE.理由如下:如图①,连接BI,∵I是△ABC的内心,∴∠1=∠2,∠3=∠4.∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,∴∠BIE=∠IBE,∴BE=IE;(2)四边形BECI是菱形.证明如下:∵∠BED=∠CED=60°,∴∠ABC=∠ACB=60°,∴BE=CE.∵I是△ABC的内心,∴∠4=12∠ABC=30°,∠ICD=12∠ACB=30°,∴∠4=∠ICD,∴BI=IC.由(1)证得IE=BE,∴BE=CE=BI=IC,∴四边形BECI是菱形.方法总结:解决本题要掌握三角形的内心的性质,以及圆周角定理.

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业

北师大初中九年级数学下册利用三角函数测高2教案
问题2、如何用测角仪测量一个低处物体的俯角呢?和测量仰角的步骤是一样的,只不过测量俯角时,转动度盘,使度盘的直径对准低处的目标,记下此时铅垂线所指的度数,同样根据“同角的余角相等”,铅垂线所指的度数就是低处的俯角.活动三:测量底部可以到达的物体的高度.“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.要测旗杆MN的高度,可按下列步骤进行:(如下图)1.在测点A处安置测倾器(即测角仪),测得M的仰角∠MCE=α.2.量出测点A到物体底部N的水平距离AN=l.3.量出测倾器(即测角仪)的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).根据测量数据,就能求出物体MN的高度.在Rt△MEC中,∠MCE=α,AN=EC=l,所以tanα= ,即ME=tana·EC=l·tanα.又因为NE=AC=a,所以MN=ME+EN=l·tanα+a.

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

北师大初中九年级数学下册三角函数的计算2教案
解在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.例5 已知cot x=0.1950,求锐角x.(精确到1′)分析根据tan x= ,可以求出tan x的值,然后根据例4的方法就可以求出锐角x的值.四、课堂练习1. 使用计算器求下列三角函数值.(精确到0.0001)sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.2. 已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)(1)sin a=0.2476; (2)cos a=0.4174;(3)tan a=0.1890; (4)cot a=1.3773.五、学习小结内容总结不同计算器操作不同,按键定义也不一样。同一锐角的正切值与余切值互为倒数。在生活中运用计算器一定要注意计算器说明书的保管与使用。方法归纳在解决直角三角形的相关问题时,常常使用计算器帮助我们处理比较复杂的计算。

北师大初中九年级数学下册三角函数的应用1教案
然后,她沿着坡度是i=1∶1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度(参考数据:2≈1.41,结果精确到0.1米).解析:作辅助线EF⊥AC于点F,根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,通过平角减去其他角从而得到∠AEF=45°,即可求出AE的长度.解:作EF⊥AC于点F,根据题意,得CE=18×15=270(米). ∵tan∠CED=1,∴∠CED=∠DCE=45°.∵∠ECF=90°-45°-15°=30°,∴EF=12CE=135米.∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°-45°-60°-30°=45°,∴AE=2EF=1352≈190.4(米).所以,娱乐场地所在山坡AE的长度约为190.4米.方法总结:解决本题的关键是能借助仰角、俯角和坡度构造直角三角形,并结合图形利用三角函数解直角三角形.

人教部编版语文八年级下册阿西莫夫短文两篇教案
预设 示例1:“板块背上驮着许多大陆,当板块向一个或另一个方向运动时,大陆也随之一起运动。”“驮”字形象地写出了大陆漂移的样子,使抽象的理论变得生动、有趣、易懂。示例2:“位于南极中心部位的南极洲是全球的大冰箱。”运用了打比方的说明方法,形象地说明了南极洲寒冷的程度和南极洲在地球生态环境中的重要位置。 示例3:“一立方英寸被压扁的沙子比一立方英寸普通的沙子要重得多。”运用作比较的说明方法,说明同体积被压扁的沙子比普通沙子重得多的特点。【设计意图】本环节设计的三个层次的语言赏析,让学生深入文本体会、学习语言简明精练、逻辑性强、幽默风趣的特点,提高学生的语言鉴赏能力,为今后的说明文写作夯实基础。四、总结拓展,激发思维所选的两篇课文就同一对象——恐龙从不同角度思考,从而发现新的论据或得出新的结论。文章给了我们一些有益的启示:不同领域的科学发现可以互相启发,从而有新的发现;要学会从不同角度思考问题。选择下面两个探讨任务之一课外完成。

人教部编版语文八年级下册口语交际即席讲话教案
预设 示例:班上分享个人读书经验大家好!既然今天是交流读书体会,那么,我想结合自己的读书体会和大家聊聊读书。一个爱读书的民族,必定是一个文化素质较高的民族;一个爱读书的人,也必定是一个文化素质较高的人。读书能开阔我们的视野,提高我们的写作水平;读书能提升自身修养,丰富我们的人生底蕴。读书是我们精神的呼吸,能让人保持平淡的心境,变得博爱而无私。为了让我们的生活和心灵变得轻盈一些,我们需要读书。那么,应该怎样读书呢?其一,要择书而读。需要的才是最适合的,读适合的书才能有良多收获。如果没有特别需要的书要读,可以读经典。经典是经过岁月沉淀下来的人类智慧的结晶,可以让我们触摸先贤的思想,以充实自身。其二,要读而有术。要对好书反复品味,将其内化吸收,然后进行批判性阅读,有自己的思想主张和拓展探究价值判断;在读书过程中与作者进行辩论,最后形成自己的思想体系,为我所用,而不是让自己的脑袋成为别人思想的“跑马场”。

人教部编版语文八年级下册庆祝奥林匹克运动复兴25周年教案
(3)推荐男女生代表各一位在全班进行演讲展示。 (4)围绕“讲”和“演”两方面的技巧,点评演讲效果。(生开展演讲活动,师指导)【设计意图】本环节通过集中梳理演讲技巧,并设计演讲技巧进行演讲展示,引导学生将理论知识逐步运用于具体的演讲实践中,提高学生的演讲能力。五、总结存储1.教师总结现代奥林匹克运动的创始人顾拜旦面对世界政治格局剧变的局面,以战略家的视野指出奥林匹克精神的内涵与价值,用诗歌般的语言阐述了奥林匹克平和自信的内涵,提出了奥林匹克运动的宗旨是教育,是面向大众,是促进和平、公平、公正。他激情澎湃地畅想美好前景,确信奥林匹克精神必将如阳光般普照大地。整篇演讲词站位高、格局广,语言庄重、典雅,值得我们用心体会。2.布置作业学校即将举行春季运动会,如果你被邀请在运动会的开幕式上作为学生代表发言,你将如何演讲?结合你对奥林匹克运动的精神的理解,写一篇300字左右的演讲词,并适当设计一些演讲技巧。

人教部编版语文八年级下册《在长江源头各拉丹动》教案
预设 第一组:(1)语言精准又生动形象,首先用长句总写各拉丹冬的变化多端,然后接连用短句,简笔勾勒各拉丹冬巍峨高大、棱角分明的特点,张弛有度,富有音乐美感。(2)用语精简而准确,形象性强,短促的句子节奏,很好地表现出冰体形状之多令人目不暇接,最后部分节奏放缓,形成一种张弛有度的音乐美,让句子又融入段落主体比较舒缓的节奏中去。第二组:(1)将自己的身体不适比喻为“小震”“大地震”,描写自己由于病痛而行动迟缓的“犹如霹雳舞的‘太空步’”,幽默之中,透露出作者乐观、坚强的精神和对探险事业的热爱。 (2)用“分外利落”形容自己拍摄冰山时跌倒骨裂的情景,好似没有痛苦一般。这幽默调侃之中,透露出作者乐观、坚强的精神。第三组:(1)“眩晕”原指一种症状,感觉到自己或周围的东西旋转,这里指“浩浩苍苍”的美景令人目不暇接,令人不知该看什么;“卖弄”原指有意显示、炫耀,含贬义,这里指大自然的无穷创造力在各拉丹冬展现得淋漓尽致。

人教部编版语文八年级下册名著导读《傅雷家书》 选择性阅读教案
评价:这段话表明傅雷朋友的角色。他把孩子当成朋友,为人生得一知己而感到兴奋、自豪。在读这段话时声音应洪亮,感情应充沛。小结:我们组还发现傅雷对傅聪的称呼有很多,如聪、聪儿、孩子、亲爱的聪、亲爱的孩子。有时两个同时用,比如“聪,亲爱的孩子!”一直以来,我们都觉得父爱不善表达,可是傅雷的这些亲昵直白的称呼表达了他对傅聪的爱,是这么的温柔,如慈母一般。所以,读这些称呼时我们要读得轻柔深情些。【设计意图】这一环节不仅能展示学生的阅读成果,还能使学生感受到阅读的成就感,并在相互交流中产生更深刻的理解和感悟,在朗读和评价中体会父爱。二、感悟成长1.解读“虎爸”师:在同学们的阅读分享中,傅雷这样一个深爱儿子的父亲形象深入人心。其实,傅雷早期对傅聪的教育是很严苛的,是一个“虎爸”的形象。我们一起来看一则小故事。

人教部编版语文八年级下册课外古诗词诵读教案
预设 “海内存知己,天涯若比邻”一反送别诗伤感悲戚的格调,体现出高远的志趣和旷达的胸怀,表明诚挚的友谊可以超越时空。此句蕴含哲理,给人以莫大的安慰和鼓舞,因此成为远隔千里的朋友间表达深情厚谊的名句。设问3:“气蒸云梦泽,波撼岳阳城”中的“蒸”和“撼”换成“滋”和“摇”好不好?为什么?预设 不好。“蒸”是蒸腾的意思,形象地描绘了洞庭湖雾气蒸腾、湖面浩渺的画面;“撼”是摇撼的意思,描绘出了洞庭湖波涛汹涌似要撼动岳阳城的雄伟壮阔的景象,且“撼”还能传达出诗人面对湖水时心胸似乎也被震荡,从而想要建功立业的主观感受。如果换成“滋”和“摇”则显得境界小、力度弱,没有这样的气势和表达效果。【设计意图】此环节主要采用问题引领的方式,一步步引导学生品味诗歌中的名句和富有表现力的字词,感受古人炼字的智慧,从而更加深入地理解诗歌情感和艺术手法。

人教部编版语文八年级下册《一滴水经过丽江》教案
【设计意图】从诗意的语言入手,引导学生关注句式节奏、抒情性、叙事性、哲理性,品析语言,从而加深对文本的理解,体会作者对丽江的热爱、赞美之情,体会作者在景物描写中隐含的思想。五、总结存储1.教师总结作者虚构一个旅游者兼讲述者——“一滴水”,用它形成时空线索,串联起丽江的自然风光、历史文化、民俗风情,并着力表现景物背后的丽江的人文精神,来抒发作者对丽江古城与自然美妙融合的赞美之情,对丽江的醇美、和谐、沉静的赞美之情,对传统与现代文明和谐交融的赞美之情,对自然万物的热爱和生命平等的意识。诗意的语言中,有强烈的抒情,有厚重的历史感,有深邃的哲思。这“一滴水”折射出的,是阿来的思想、灵魂。2.布置作业(1)模仿本文的写法,写一篇不少于600字的随笔,选择一个恰当的视角,跨越时空,全面多角度展现家乡的自然风光、历史文化、风土人情。(2)课外阅读阿来的《大地的阶梯》,体会融景物、历史、感悟、思考于一体的游记风格。






