-

道德与法治八年级下册理解权利义务7作业设计
②积极参与国家事务和社会事务的管理③在享有劳动权利的同时,也履行了劳动的义务④既获得了劳动报酬,也为国家和社会作出了贡献 A.①② B.②③ C.①④ D.③④11.2020 年 6 月 19 日,国家林业和草原局、农业农村部发布通知,就《国家重点 保护野生动物名录》公开征求意见。画眉、啄木鸟、田螺等被增列入名录中,55 个鲸豚类和猛禽类等物种保护等级升级。作为中学生,保护野生动物是:( ) A.法律禁止做的,我们坚决不做 B.法律要求做的,我们必须去做C.道德要求做的,我们积极去做 D. 自觉自愿行为,可做也可不做 12.遇到交通肇事,不按照正常程序处理,而是采取极端的方式解决。陕西省榆 林市公安局榆阳分局镇川派出所,对涉嫌非法入侵他人住宅的 5 名嫌疑人刑拘。 这表明:( )①公民的住宅不受侵犯②禁止非法搜查或者非法侵入公民的住宅③公民权利如果受到损害,要懂得依照法定程序维护权利④我们在行使自由和权利的时候,不得损害其他公民的合法的自由和权利
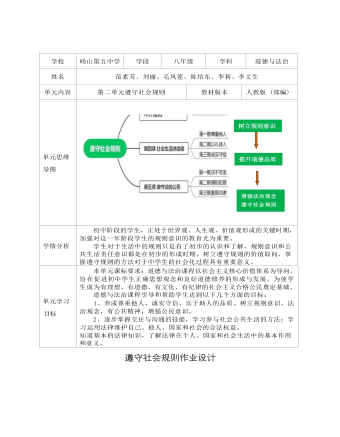
道德与法治八年级下册遵守社会规则作业设计
作业设计是老师布置给学生学习任务的设计,是教学设计的有机组 成部分。它以学习目标为起点,以学习内容为依托,以学习评价为保障, 以发展学生素养为最高标准。作业设计的要素包括作业内容、时间要求、 设计意图、作业分析及作业评价。我们八年级道德与法治组将单元作业 设计为三部分,第一部分是课时作业,本部分通过设置习题和活动,达 道巩固知识立德树人的目标。第二部分是单元作业,主要是为了检测学 生是否达到了单元学习目标,这部分重点考查学生对基础知识的掌握情 况。第三部分是特色作业,增强家国情怀,提高主人翁意识,更加注重 学生的能力提升。进入八年级,知识内容不断加深,同学们在学习方面面临着更大的 挑战,一部分学生因此产生畏难情绪,感觉学习吃力,如果在作业设置 方面,设置的作业量过大或过难,容易让学生彻底失去学习的兴趣,从 而放弃学习。

山东省泰安市2017年中考历史真题试题(毕业年级,含答案)
材料一 公元l世纪时,古罗马博物学家普林尼在其被誉为百科全书式的著作《自然史》中把中国叫做“丝之国”,古罗马的贵族都以穿着中国丝绸为荣。他还说中国出产的钢很硬,质地很好。17世纪以来,许多欧洲国家的宫廷和王公贵族更是竟相购藏中国的瓷器、漆器和丝绸、刹绣,甚至不惜重金到中国定做,运回国内珍藏起来。(l)材料一反映了古丝绸之路对罗马上层社会生活的影响。清指出汉代丝绷之路的起止点,并说明其开通的重大历史意义。(4分)

人教版新课标高中地理必修2第二章第二节不同等级城市的服务功能教案
1.了解我国城市等级划分的标准,知道不同国家和地区城市等级划分的标准是不同的。2.了解不同的城市等级其城市地域结构不同,提供的服务种类和服务范围是不同的。联系城市地域结构的有关理论,说明不同规模城市服务功能的差异。3.了解不同等级城市服务范围的嵌套理论,了解不同等级城市空间分布特点。教学重点:1.了解我国城市等级划分的标准2.了解不同的城市等级其城市地域结构不同,提供的服务种类和服务范围是不同的。教学难点::不同等级城市服务范围的嵌套理论教具准备:多媒体教学方法:比较分析法、图示法、讲述法、列表对比法教学过程:第一课时导入新课:我们生活在不同的城市,如广州、佛山、西樵等,我们知道,这些城市有大小之分,也就是说城市等级是是不同的,那么城市的等级是如何划分的呢?不同等级城市的服务功能如何呢?这就是我们今天要探讨的第二节

北师大初中九年级数学下册二次函数y=ax2+bx+c的图象与性质1教案
解析:(1)已知抛物线解析式y=ax2+bx+0.9,选定抛物线上两点E(1,1.4),B(6,0.9),把坐标代入解析式即可得出a、b的值,继而得出抛物线解析式;(2)求出y=1.575时,对应的x的两个值,从而可确定t的取值范围.解:(1)由题意得点E的坐标为(1,1.4),点B的坐标为(6,0.9),代入y=ax2+bx+0.9,得a+b+0.9=1.4,36a+6b+0.9=0.9,解得a=-0.1,b=0.6.故所求的抛物线的解析式为y=-0.1x2+0.6x+0.9;(2)157.5cm=1.575m,当y=1.575时,-0.1x2+0.6x+0.9=1.575,解得x1=32,x2=92,则t的取值范围为32<t<92.方法总结:解答本题的关键是注意审题,将实际问题转化为求函数问题,培养自己利用数学知识解答实际问题的能力.三、板书设计二次函数y=ax2+bx+c的图象与性质1.二次函数y=ax2+bx+c的图象与性质2.二次函数y=ax2+bx+c的应用

北师大初中九年级数学下册二次函数y=ax2+bx+c的图象与性质2教案
1.使学生掌握用描点法画出函数y=ax2+bx+c的图象。2.使学生掌握用图象或通过配方确定抛物线的开口方向、对称轴和顶点坐标。让学生经历探索二次函数y=ax2+bx+c的图象的开口方向、对称轴和顶点坐标以及性质的过程,理解二次函数y=ax2+bx+c的性质。用描点法画出二次函数y=ax2+bx+c的图象和通过配方确定抛物线的对称轴、顶点坐标理解二次函数y=ax2+bx+c(a≠0)的性质以及它的对称轴(顶点坐标分别是x=-b2a、(-b2a,4ac-b24a)一、提出问题1.你能说出函数y=-4(x-2)2+1图象的开口方向、对称轴和顶点坐标吗?(函数y=-4(x-2)2+1图象的开口向下,对称轴为直线x=2,顶点坐标是(2,1)。2.函数y=-4(x-2)2+1图象与函数y=-4x2的图象有什么关系?(函数y=-4(x-2)2+1的图象可以看成是将函数y=-4x2的图象向右平移2个单位再向上平移1个单位得到的)

北师大初中九年级数学下册二次函数y=x2和y=-x2的图象与性质2教案
【教学目标】(一)教学知识点能够利用描点法作出函数 的图象,并根据图象认识和理解二次函数 的性质;比较两者的异同.(二)能力训练要求:经历探索二次函数 图象的作法和性质的过程,获得利用图象研究函数性质的经验.(三)情感态度与价值观:通过学生自己的探索活动,达到对抛物线自身特点的认识和对二次函数性质的理解. 【重、难点】重点 :会画y=ax2的图象,理解其性质。难点:描点法画y=ax2的图象,体会数与形的相互联系。 【导学流程】 一、自主预习(用时15分钟)1.创设教学情境我们在教学了正比例函数、一次函数、反比例函数的定义后,都借助图像研究了它们的性质.而上节课我们所学的二次函数的图象是什么呢?本节课我们将从最简单的二次函数y=x2入手去研究

北师大初中九年级数学下册二次函数y=a(x-h)2+k的图象与性质1教案
(3)设点A的坐标为(m,0),则点B的坐标为(12-m,0),点C的坐标为(12-m,-16m2+2m),点D的坐标为(m,-16m2+2m).∴“支撑架”总长AD+DC+CB=(-16m2+2m)+(12-2m)+(-16m2+2m)=-13m2+2m+12=-13(m-3)2+15.∵此二次函数的图象开口向下,∴当m=3米时,“支撑架”的总长有最大值为15米.方法总结:解决本题的关键是根据图形特点选取一个合适的参数表示它们,得出关系式后运用函数性质来解.三、板书设计二次函数y=a(x-h)2+k的图象与性质1.二次函数y=a(x-h)2+k的图象与性质2.二次函数y=a(x-h)2+k的图象与y=ax2的图象的关系3.二次函数y=a(x-h)2+k的应用要使课堂真正成为学生展示自我的舞台,还学生课堂学习的主体地位,教师要把激发学生学习热情和提高学生学习能力放在教学首位,为学生提供展示自己聪明才智的机会,使课堂真正成为学生展示自我的舞台.充分利用合作交流的形式,能使教师发现学生分析问题、解决问题的独到见解以及思维的误区,以便指导今后的教学.

北师大初中九年级数学下册二次函数y=x2和y=-x2的图象与性质1教案
雨后天空的彩虹、河上架起的拱桥等都会形成一条曲线.问题1:这些曲线能否用函数关系式表示?问题2:如何画出这样的函数图象?二、合作探究探究点:二次函数y=x2和y=-x2的图象与性质【类型一】 二次函数y=x2和y=-x2的图象的画法及特点在同一平面直角坐标系中,画出下列函数的图象:(1)y=x2;(2)y=-x2.根据图象分别说出抛物线(1)(2)的对称轴、顶点坐标、开口方向及最高(低)点坐标.解析:利用列表、描点、连线的方法作出两个函数的图象即可.解:列表如下:x y) -2 -1 0 1 2y=x2 4 1 0 1 4 y=-x2 -4 -1 0 -1 -4 描点、连线可得图象如下:(1)抛物线y=x2的对称轴为y轴,顶点坐标为(0,0),开口方向向上,最低点坐标为(0,0);(2)抛物线y=-x2的对称轴为y轴,顶点坐标为(0,0),开口方向向下,最高点坐标为(0,0).方法总结:画抛物线y=x2和y=-x2的图象时,还可以根据它的对称性,先用描点法描出抛物线的一侧,再利用对称性画另一侧.

北师大初中九年级数学下册二次函数y=ax2和y=ax2+c的图象与性质1教案
变式训练:见《学练优》本课时练习“课堂达标训练”第5题【类型二】 在同一坐标系中判断二次函数和一次函数的图象在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为()解析:∵一次函数和二次函数都经过y轴上的点(0,c),∴两个函数图象交于y轴上的同一点,故B选项错误;当a>0时,二次函数的图象开口向上,一次函数的图象从左向右上升,故C选项错误;当a<0时,二次函数的图象开口向下,一次函数的图象从左向右下降,故A选项错误,D选项正确.故选D.方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.变式训练:见《学练优》本课时练习“课后巩固提升” 第4题【类型三】 二次函数y=ax2+c的图象与三角形的综合

大班装饰画教案:蝴蝶和鸟
活动准备: 1、幼儿用书人手一册 2、记号笔每人一支,油画棒每桌一盘。 3、轻音乐和“蝴蝶飞”的音乐。活动过程: 一、猜谜引题: 两根胡须头上翘, 身穿五彩花袍袍, 劳动辛苦我不怕, 跳起舞来我最好。(蝴蝶) 二、通过图片欣赏各种蝴蝶。 1、欣赏图片 提问,了解蝴蝶的外形特征: 1) 蝴蝶有几对翅膀?(两对翅膀)哪对翅膀大?(前翅大,后翅小) 2) 蝴蝶有没有眼睛?(有一双小眼睛)头上还有什么?(还有一对触角) 3) 蝴蝶的身体是怎样的?(细细长长的) 4) 蝴蝶有几只脚? 2、教师引导:蝴蝶身上还有五颜六色的花纹和图案呢,让我们一起来看看这些美丽的蝴蝶吧!找一找,你最喜欢哪一只!他们的图案是不是左右对称的?颜色呢? 幼儿欣赏图片。 3、幼儿自由讲述不同图案和颜色的蝴蝶。 三、幼儿装饰画:蝴蝶。 1、亲爱的小朋友们: 蝴蝶王国马上要举办一次化妆舞会,但是王国的蝴蝶们没有漂亮的衣服,现在想请你们小朋友帮助我们,你们愿意吗? 2、每人一只纸蝴蝶,请幼儿装饰。 1) 引导幼儿利用左右对称的方法装饰。 2) 鼓励幼儿大胆想象不同的线条装饰,并大胆用色。

大班美术教案:装饰盘子
1、学习中心及边缘连续装饰的技能,能用简单的图案装饰盘子。2、引导幼儿感受和表现连续对称的美。3、培养幼儿耐心、细致、整洁的习惯。活动重、难点:掌握边缘连续装饰方法。二、 活动准备:1、水彩笔、彩纸、废旧图书、雪花片、圆形纸盘若干。2、教师制作的盘子展。3、投影仪、各种盘子录像。

装扮舞台课件教案
2、积累使用剪刀的经验。3、幼儿在活动中愉快地进行创造、表演。活动准备:1、铅画纸、各色皱纹纸、蜡光纸、卡纸、即时贴。2、水粉颜料、各色油画棒、牙刷、杯托、纸杯、擦手的湿毛巾、剪刀、糨糊、双面胶、透明胶、小箩筐(人手一份)。3、音乐磁带、各种花盆等。活动过程:一、谈话,激发幼儿活动的兴趣最近我发现我们小朋友都很喜欢表演,今天幼儿园里来了许多客人老师,我们一起来装扮舞台,把你们的本领表演给他们看,好吗?让客人老师们看一看,哪位小朋友的手儿最灵巧,最能干。

装饰画 “手帕”课件教案
2会用花纹,格子或图样对手帕进行装饰,敢大胆的选色,装饰,自己设计手帕,注意色彩的多样.教学准备: 各式图案,花纹的手帕,作业纸(方形,手帕状),幼儿人手一盒蜡笔及颜料(红,黄,蓝,绿),毛笔.教学过程:一. 出示各式手帕,让幼儿欣赏.1. 这是什么?(手帕)它们有什么不一样的地方?(花纹不一样)2. 花纹什么地方不一样?(有的是围着手帕四周一圈,有的只有一个角上有花纹,有的在中间有图案;或是图案不一样,有的是动物,有的是花,有的是格子-----) 二. 装饰手帕,幼儿作业1. 我们今天也来画手帕,你喜欢什么样的手帕?(幼儿讲述).

人教版新课标小学数学一年级下册两位数减一位数和整十数(不退位)教案
一、教学内容:两位数减一位数和整十数(不退位)(课本第67页)。二、教学目标:1、知识与技能:让学生经历探索两位数减一位数和整十数(不退位)的计算方法的过程,掌握计算方法,能正确地口算。2、过程与方法:让学生经历自主探索、动手操作、合作交流等方式获得新知的过程,积累数学活动的经验,体会数学知识与日常生活的密切联系,增强应用意识。3、情感态度与价值观:进一步培养学生学习数学的热情,以及积极思考、动手实践并与同学合作学习的态度。三、教学重点:掌握两位数减一位数和整十数(不退位)的口算方法。四、教学难点:理解算理,把握两位数减一位数与两位数减整十位数在计算过程中的相同点与不同点。五、教具准备:课件、题卡、等。六、教学过程:(一)、创设情境,提出问题。

人教版新课标小学数学三年级下册一位数除三位数(商是两位数且有余数)教案2篇
二、互动交流,理解算法1.出示教科书第22页的情境图,提问:他们在干什么?你获得了什么信息?能提出什么问题?怎样列式?2.师:今天我们就学习一位数除三位数的计算方法。(板书课题:一位数除三位数)3.师:怎样计算238÷6呢?你能用估算的方法估计出大致结果吗?4.学生尝试独立完成例3的竖式计算。师:在这道题中被除数最高位上是2个百,2个百除以6,商不够1个百怎么办?师:谁能说一说商3个十的3写在商的什么位置上?为什么?教师边板演边说明:用除数6去乘3个十,积是18个十,表示被除数中已经分掉的数,写在23的下面。23减18得5,表示十位上还剩5个十。师:接下来该怎么办?(把被除数个位上的8落下来,与十位上的5合起来继续除。)师:最后结果是多少?5.启发学生想一想:如果一本相册有24页,一本相册能插得下这些照片吗?2本呢?

中班科学:水果里的图案课件教案
活动准备: 各种常见水果若干、布袋、塑料水果刀、盘子、猕猴桃、黄桃、圣女果活动过程:一、摸水果 教师出示装有各种幼儿熟悉的水果的自制摸宝袋,请幼儿摸摸、说说自己从袋里摸到的是什么水果,它的外形是怎样的?它的味道如何?有没有香味?二、出示水果图案 教师出示某一水果的切面,请幼儿观察它的图案。

频率的稳定性教案教学设计
活动内容:教师首先让学生回顾学过的三类事件,接着让学生抛掷一枚均匀的硬币,硬币落下后,会出现正面朝上、正面朝下两种情况,你认为正面朝上和正面朝下的可能性相同吗?(让学生体验数学来源于生活)。活动目的:使学生回顾学过的三类事件,并由掷硬币游戏培养学生猜测游戏结果的能力,并从中初步体会猜测事件可能性。让学生体会猜测结果,这是很重要的一步,我们所学到的很多知识,都是先猜测,再经过多次的试验得出来的。而且由此引出猜测是需通过大量的实验来验证。这就是我们本节课要来研究的问题(自然引出课题)。

角平分线的性质教案教学设计
这是本节课的重点。让同学们将∠aob对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,请同学们观察并思考:后折叠的二条折痕的交点在什么地方?这两条折痕与角的两边有什么位置关系?这两条折痕在数量上有什么关系?这时有的同学会说:“角的平分线上的点到角的两边的距离相等”.即得到了角平分线的性质定理的猜想。接着我会让同学们理论证明,并转化为符号语言,注意分清题设和结论。有的同学会用全等三角形的判定定理aas证明,从而证明了猜想得到了角平分线的性质定理。

平行线的判定定理教案教学设计
问题1:你能证明“两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行”这个命题的正确性吗?已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b. 问题2:你能证明“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题的正确性吗?已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b

