-
九年级上册道德与法治民主与法治1作业设计
2.认同民主是具体的, 能够根据本国的国情看待民主实现的方式, 积极主动 参与民主生活,培育民主意识,形式民主权利。3.体会法治在社会中的作用, 认同法治价值观, 感受法治中国的进步, 坚定 走中国特色社会主义法治道路的信念。4.感受见识法治中国是全体社会成员的共同责任, 并树立法治意识, 自觉尊 法学法守法用法,践行法治精神。四、单元作业设计思路(一) 单元作业设计基本原则1.作业设计应全面地反映知识与技能、过程与方法、情感与价值这个三维目 标。在有效作业设计中, 应重视教材学习材料的深度挖掘编写出相应题目, 以促 进学生从课堂学习中获取必要的认识经验, 通过过程获得感受, 通过活动得到一 定的体会,通过探索得一些感悟。2.作业设计应考虑学生的参与度。分层设计, 让不同层次的学生有选择地训 练,可有效地避免不做练习或抄作业现象,大大提高学生的参与度。3.控制作业的时间限度, 少时高效。控制课后作业时间, 关注学生身心健康, 促进学生全面发展。
九年级上册道德与法治富强与创新2作业设计
【作业分析】本题考查创新改变生活。防雨神器自动收晾衣服的灵感来源是下 雨忘记收衣服被批评,体现创新是来源于生活、来源于实践。“智能晴雨棚”打 破了传统的只能晾衣服的常规。而由教材内容可知,创新是改革开放的生命, 改革在不断创新中提升发展品质,所以②错误;故本题选 C2. (改编) 利用“安康码”自动定位,即可监测附近新冠肺炎感染病例发病点; 通过输入自己的手机号码,即可通过“通信大数据卡”判断自己是否到访过高 危地区;通过皖事通 APP“密接人员自查”即可查询自己是否曾与新冠肺炎感染 患者接触……疫情发生以来,大数据、健康码、无人机、机器人、测温仪等众 多科技创新成果纷纷登场,助力疫情防控,提高了抗击疫情的精准化水平。这 表明 ( )①标志着我国已经成为科技强国②实施创新驱动发展战略成效显著③创新应成为国家发展进步的中心工作④创新的目的是增进人类福祉,让生活更美好A.①② B.②③ C.①④ D.②④【评价实施主体】教师【评价标准】D【作业分析】本题考查科技创新改变生活中创新的重要性。我国现在还不是科 技强国,但科技自主创新能力不断增强,所以①说法错误。
九年级上册道德与法治富强与创新7作业设计
作业 2 观看视频设计分析:学生通过观看 2022 年中国冬奥会厨房机器人感 受到祖国充满创新的高科技风格, 感受祖国的强大, 激发学生的民族自豪感, 自 信心。作业 2 观看视频设计意图:激发学生的学习的热情, 培养创新精神, 提高创 新能力,树立远大的理想。(五) 作业实施与反思作业 1:通过新闻点评, 感受祖国的航天事业的蓬勃发展, 激发学生的爱国 情怀, 考查学生对于创新价值的理解, 对于国家创新文化的自豪感以及对于国家 创新发展的自信。考查学生辩证看待问题的能力和自觉践行创新的能力, 激励学 生有意识地在日常生活中培养自己的创新能力。作业 2:通过观看视频, 2022 年中国冬奥会厨房机器人,智能化运用到生 活中, 机器人学生更关注, 更有兴趣, 从而激发学生学习的热情, 培养学生创新 的热情, 提高创新的能力。感受中国创新成就中培养民族自豪感,形成国家观、 世界观,培养民族担当意识,树立远大理想。
九年级上册道德与法治和谐与梦想1作业设计
10.2022 年 4 月 16 日 9 时 56 分,太空“出差”的 3 名宇航员安全顺利出舱,重 回地球的怀抱,神舟十三号载人飞船实现了多个“首次”,不断刷新中国航天 科技的新纪录,展现了中国航天科技的新高度,再次向世界展现出自信和自强。 这份自信的根源是 ( )A.弘扬了中国精神 B.坚持了中国特色自主创新道路C.凝聚了中国力量 D.坚持了中国特色社会主义道路、理论、制度和文化二、非选择题【春晚传情 中华同心】11.“你是中国的母亲,孕育着中国的奇迹,牵系千百年的呼吸,澎湃着中国的 生命 … … ”,虎年春晚,来自海峡两岸暨香港、澳门的四位歌手共同演唱的歌曲 《黄河长江》,唱得大家心潮澎湃。歌曲中,情感深沉的歌词,字字饱含着对祖 国山河的热爱;高亢激昂的旋律,传递出黄河长江穿越古今的力量。(1) 海峡两岸和香港、澳门的四地歌手在春晚的舞台上携手共唱、深情演绎, 向我们传递了怎样的信息?(2) 为了促进海峡两岸和香港、澳门四地的文化相融,你可以提出哪些合理化 建议?
九年级上册道德与法治民主与法治4作业设计
法治与我同行。宿州市某校 901 班举行“法治头条”交流活动, 同学们分享 了许多法治新闻。◇2016 年 9 月 12 日, 国务院新闻办公室发布《中国司法领域人权保障的新 进展》白皮书。白皮书指出, 中国落实罪刑法定、疑罪从无、非法证据排除等法 律原则,积极防范和纠正冤假错案。◇2018 年 3 月 11 日, 十三届全国人大一次会议通过《中华人民共和国宪法 修正案》。◇2020 年 10 月 17 日,十三届人大常委会第二十二次会议通过《中华人民 共和国生物安全法》,使我国生物安全风险防控有法可依。◇2021年 8 月 20 日, 十三届全国人大常委会第三十次会议表决通过《中华 人民共和国个人信息保护法》,这部法律充分回应了社会关切,为破解个人信息 保护中的热点难点问题提供了强有力的法律保障。◇2022 年 1 月 1 日, 由十三届人大常委会第三十一次会议表决通过的《中 华人民共和国家庭教育促进法》正式实施。该法将家庭教育由传统的“家事”上 升为新时代的重要“国事”。1.探究与分享:请学生思考或分组讨论每一条法治新闻对社会生活的影响, 分析其进步之处,并交流分享自己的感悟。2.查找资料,说一说保护未成年人的法律有哪些。3.制作一份“法治与我同行”的手抄报,展示在学校或班级的法治栏内。要求: 在制作手抄报的过程中, 思考: (1) 法治的作用; (2) 优秀手抄报的 评判标准。

九年级上册道德与法治民主与法治3作业设计
(三) 学情分析初中阶段的学生正处在世界观、人生观、价值观形成的关键时期, 加强对这 一年龄段学生的法治教育尤为重要。随着学生生活范围的延展和能力的提升, 本课程的学习逐步扩展到国家和社 会。从生活经验看, 大部分中学生有参与班干竞选、给班级或学校提建议的经验。 从知识储备看, 学生在八年级下册已经学习了我国的根本政治制度、基本政治制 度, 故学习本课知识已经具备了一定的理论基础。但如何理解民主, 还需要通过 不断的学习来建立认同。另外七八年级也打下了一定的法律基础, 学生已经初步 了解个人的成长和参与社会生活必备的基本法律常识。本单元第三课通过介绍社会主义民主制度的确立过程, 中国特色社会主义民 主的本质和实现方式, 引领学生理解社会、参与公共生活, 帮助学生认同民主的 价值,引导学生做负责任的公民。第四课阐释法治是什么、回顾法治中国的历程、 明确为什么选择中国特色社会主义法治道路、怎样建设法治中国及初中生在法治 中国的建设中应扮演怎么样的角色等问题, 帮助学生认识法治中国的进程, 引导 学生正确看待法治中国建设进程中出现或可能出现的问题, 进而把法治作为基本 的生活方式,在实践中培育法治观念。

部编版语文七年级上册《从百草园到三味书屋》说课稿
2、教学目标根据新课程理念,根据单元要求与课文教材特点,我确定以下三大目标:⑴知识目标:掌握重点字词,了解、把握课文内容、品味语言。⑵能力目标:学会小组自主合作探究,学会分析散文与语段、语言的方法。⑶情感目标:体会童年生活的情趣,关注自身的生活与成长,同时增加学生学习语文的兴趣,全面提高学生语文综合素养。3、教学重难点:本课是学生本学期的第一篇课文,也是本册、本单元的的第一篇课文。在上学期的语文学习的基础上,根据单元语课文特点,因此要把指导学生养成语文学习习惯与掌握学习方法作为本课教学重点。从理解课文方面看,难点在于让学生理解作者是怎样将美好的童年生活内容与情趣表现出来的,所以要将此点作为难点来突破。由此可见,两者相辅相成,互相渗透,而利用课件为学生提供形象生动的画面与针对性的探讨,创设情境加强对学生学习方法的指导与学生主体自主学习、合作探讨是突破本课教学重难点的关键。

部编版语文七年级上册《赫尔墨斯和雕像者》说课稿
一、说教材《赫尔墨斯和雕像者》选自人教版七年级上册第六单元《寓言四则》中的第一则寓言,本单元主要是一些有趣的故事,通过故事揭示道理。学情分析:学生在小学已经学过一些寓言故事的基础上,能够联系自己的生活体验积极思考和表达自己的观点。(根据新课标要求、寓言的特征和学生的实际情况)二、说教学目标知识与能力目标:了解寓言以及《伊索寓言》的知识;过程与方法目标:品味描写人物心理变化等细节描写,分析赫尔墨斯的性格特征;情感态度与价值观目标:正确理解寓意,树立正确的人生处事态度。三、说重难点(本单元要求:学习《伊索寓言》时重在让学生揣摩人物的语言、表情。)重点:揣摩人物的心理变化等细节描写。难点:多元理解寓意,培养学生发散思维。

部编版语文七年级下册《外国诗两首(假如生活欺骗了你 未选择的路)》教案
写作背景这首诗写于普希金被沙皇流放的日子里,是以赠诗的形式写在他的邻居奥希泊娃的女儿叶甫勃拉克西亚·尼古拉耶夫娜·伏里夫纪念册上的。那里俄国革命正如火如荼,诗人却被迫与世隔绝。在这样的处境下,诗人却没有丧失希望与斗志,他热爱生活,执着地追求理想,相信光明必来,正义必胜。(三)、问题探究1、“假如生活欺骗了你”指的是什么?指在生活中因遭遇艰难困苦甚至不幸而身处逆境。作者写这首诗时正被流放,是自己真实生活的写照。2、诗人在诗中阐明了怎样的人生态度?请结合你感受最深的诗句说说你曾有过的体验。诗中阐明了这样一种积极乐观的人生态度:当生活欺骗了你时,不要悲伤,不要心急;在苦恼的时候要善于忍耐,一切都会过去,我们一定要永葆积极乐观的心态;生活中不可能没有痛苦与悲伤,欢乐不会永远被忧伤所掩盖,快乐的日子终会到来。

关于自信自强的国旗下的讲话
第一篇:国旗下的讲话:人生应自信、自强矫健的苍鹰扇动着双翅,翱翔在高空,无畏的目光点亮前进的道路,寻找自己的天堂。它自信,得到诗人的讴歌;它自强,受到英雄的敬仰。苍鹰尚且如此,满腔热血的我们又该如何主宰自己的人生呢?生活中有这样一个故事:一位中国留学生以优异的成绩考入了美国一所著名的大学。怀揣着梦想,他告别了父母,远离了家乡。但是,入学不久,他就提出了退学。理由很简单:生活饮食不习惯,父母所给的生活费已经花完。回到家乡的机场,迎接他的是年近花甲的父亲,当他看到久违的父亲就高兴的扑过去,父亲一腿部,儿子扑了个空,一个趔趄摔倒在地。父亲看着尴尬的儿子深情的说:“孩子,这个世界上没有任何人可以做你的靠山,你若想在激烈的竞争中立于不败之地,任何时候都不能丧失那个叫自立、自信、自强的生命支点,一切全靠你自己。”说完,父亲塞给儿子一张返程机票。这位学生没跨进家门就直接登上了返回美国的航班,返校不久,他获得了学院里的最高奖学金,且有数篇论文陆续发表在有国际影响的刊物上。

国旗下的讲话:乐观自信我能行
各位老师,同学:大家早上好!我今天在国旗下讲话的题目是《乐观自信我能行》。有人说:乐观自信是一粒生命的种子,深藏在人心里,随时都可能发芽,并开出绚烂夺目的花朵。更有人说:乐观自信是一缕阳光,时刻照亮着我们的每一天,生活因此而幸福快乐。这些话语同学们或许不是很懂,老师我还是先给大家讲个故事吧!故事的题目叫———《小板凳》。世界著名大科学家爱因斯坦上小学时,有一次上劳动课,同学们都交上了自己的作品,像泥鸭子啊、布娃娃啊,小汽车啊等等。惟有爱因斯坦没有按时交上作品,直到第二天,他才送去一只做得很粗糙的小板凳。老师看了很不满意地说:“我想世上不会有比这更差的小板凳了。”爱因斯坦回答说:“有的。”他不慌不忙地从课桌里拿出两只小板凳,举起左手说:“这是我第一次做的。”又举起右手说:“这是我第二次做的,……刚才交的,是我第三次做的,虽然它不能使人满意,但总比这两只强一些。在我眼里,第三只小板凳是最漂亮的了!”这是一个多么伟大的回答啊!同学们,正是爱因斯坦拥有“一次比一次做得好”这样的乐观自信,才促使他成为一名伟大的科学家。
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
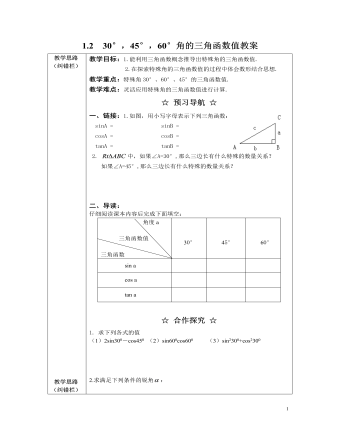
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中九年级数学下册弧长及扇形的面积教案
1.了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用;(重点)2.通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长l=nπR180和扇形面积S扇=nπR2360的计算公式,并应用这些公式解决一些问题.(难点)一、情境导入如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗(π 取3.14)?我们容易看出这段铁轨是圆周长的14,所以铁轨的长度l≈2×3.14×1004=157(米). 如果圆心角是任意的角度,如何计算它所对的弧长呢?二、合作探究探究点一:弧长公式【类型一】 求弧长如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()
北师大初中九年级数学下册商品利润最大问题2教案
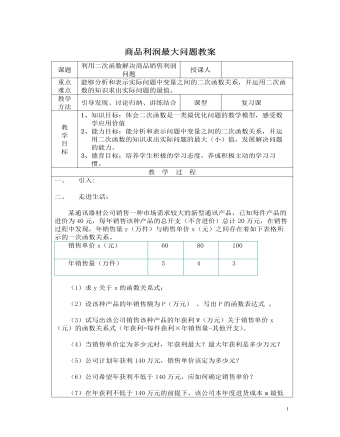
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册切线的判定及三角形的内切圆教案
解析:(1)连接BI,根据I是△ABC的内心,得出∠1=∠2,∠3=∠4,再根据∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,得出∠BIE=∠IBE,即可证出IE=BE;(2)由三角形的内心,得到角平分线,根据等腰三角形的性质得到边相等,由等量代换得到四条边都相等,推出四边形是菱形.解:(1)BE=IE.理由如下:如图①,连接BI,∵I是△ABC的内心,∴∠1=∠2,∠3=∠4.∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,∴∠BIE=∠IBE,∴BE=IE;(2)四边形BECI是菱形.证明如下:∵∠BED=∠CED=60°,∴∠ABC=∠ACB=60°,∴BE=CE.∵I是△ABC的内心,∴∠4=12∠ABC=30°,∠ICD=12∠ACB=30°,∴∠4=∠ICD,∴BI=IC.由(1)证得IE=BE,∴BE=CE=BI=IC,∴四边形BECI是菱形.方法总结:解决本题要掌握三角形的内心的性质,以及圆周角定理.

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册确定二次函数的表达式1教案
解析:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,根据对称轴是x=-3,求出b=6,即可得出答案;(2)根据CD∥x轴,得出点C与点D关于x=-3对称,根据点C在对称轴左侧,且CD=8,求出点C的横坐标和纵坐标,再根据点B的坐标为(0,5),求出△BCD中CD边上的高,即可求出△BCD的面积.解:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,∴c-4b=-19.∵对称轴是x=-3,∴-b2=-3,∴b=6,∴c=5,∴抛物线的解析式是y=x2+6x+5;(2)∵CD∥x轴,∴点C与点D关于x=-3对称.∵点C在对称轴左侧,且CD=8,∴点C的横坐标为-7,∴点C的纵坐标为(-7)2+6×(-7)+5=12.∵点B的坐标为(0,5),∴△BCD中CD边上的高为12-5=7,∴△BCD的面积=12×8×7=28.方法总结:此题考查了待定系数法求二次函数的解析式以及二次函数的图象和性质,注意掌握数形结合思想与方程思想的应用.

北师大初中九年级数学下册三角函数的计算2教案
解在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.例5 已知cot x=0.1950,求锐角x.(精确到1′)分析根据tan x= ,可以求出tan x的值,然后根据例4的方法就可以求出锐角x的值.四、课堂练习1. 使用计算器求下列三角函数值.(精确到0.0001)sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.2. 已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)(1)sin a=0.2476; (2)cos a=0.4174;(3)tan a=0.1890; (4)cot a=1.3773.五、学习小结内容总结不同计算器操作不同,按键定义也不一样。同一锐角的正切值与余切值互为倒数。在生活中运用计算器一定要注意计算器说明书的保管与使用。方法归纳在解决直角三角形的相关问题时,常常使用计算器帮助我们处理比较复杂的计算。

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值





