-

优秀班主任个人工作心得体会参考范文
第一:不要吝啬对学生的爱。爱是溶化剂,爱是桥梁。要想让学生爱你,首先你应该付出你的爱。为了做到这点,我把关爱渗透到平时。我从不吝啬我的爱。比如:帮学生整理衣领,拍拍学生的头,学生生病时温柔的目光,关切的话语,递上的一杯热水。天气变了,我会及时提醒学生添加衣物,注意用火、用电安全。特别是周一第四节课和周六学生该回家时,我都不忘提醒学生下楼慢点,路上注意安全,会说:周一我会迎接同学们返校的。我是老师也是母亲,我的关爱发自心底,出自真诚。我在尽力做到:随风潜入夜,润无心无声。

个人银行合规学习心得体会优质范文
第一,要把以"客户为中心"的理念贯穿于我们工作的始终。"基础牢固,稳如泰山;基础不牢,地动山摇"。风险的防范与控制,说到底是人的因素起着重要作用,客户创造市场,客户创造价值,客户是我们的效益之源,是我们的衣食父母,有了客户,我们的业务才有发展,员工的价值才能够体现。 如果每个岗位的员工都能严格要求、严格规范、严格标准、严格执行规章制度,业务操作中的风险就会得到有效的遏制。要在全体员工中大力倡导、深入宣传价值最大化、资本约束、全面风险管理、风险与收益平衡、内控优先等先进理念,让全体员工了解资产质量与经济增加值、与薪酬分配的关系,自觉转变观念,将自身工作作为第一道防线纳入到风险控制体系中,引导和带领全行员工形成规范操作,防范风险的良好氛围,真正把为前台、为基层、为客户服务当作提升风险与回报管理水平的出发点和归宿,就能有效提高我行风险管理和内控政策、法规、制度的执行和落实,全面加强风险管理和内控建设具有不可替代的重要作用。

个人奋进网上祭英烈心得体会例文8篇
如今的我们,沐浴着阳光,在明亮的教室里读书,在知识的殿堂中尽情遨游;如今的我们,生活在一个没有战争的和平世界中,孩子们,大人们脸上都展露会心的微笑;如今的我们,生活富裕,想买什么就买什么,零食、饮料样样不缺……大家可曾想过,如今的幸福生活,是如何得来的? 是战士们用自己的鲜血换来的!鲜血染红了五星红旗,染红了红领巾,染红了我们每一个人的心!战场上抛头颅,洒热血,勇往直前,将敌人全部消灭:黄继光用身体挡住敌人的子弹;狼牙山五壮士用生命换来了群众的安全;董存瑞舍身炸碉堡;刘胡兰面对刀架不屈服,未满14岁便光荣牺牲……革命先烈三天三夜也讲不完!

学生个人两红两优表彰大会心得精品例文
随着自己的不断长大,发现我们身上的责任也越来越大,因为我们是新时代的青年,我们要做好自己的责任,要努力学习。都说我们是垮掉的一代,实际上并不是,我们是抗疫的主力军,冲在最前面为国家人民保驾护航! 共青团建团百年作为新时代的的青年,我们要树立爱国主义精神,国家的前途,民族的命运,人民的幸福,是当代中国青年必须和必将承担的重任。 以便以后为国家和人民献上自己的一份力,在不远的将来我们国家会越来越好,中华民族屹立于世界民族之林,实现中华民族伟大复兴。

大学生弘扬五四精神学习个人心得体会例文
新时代青年应该立鸿鹄之志,展骐骥之跃,青年当系好人生第一粒扣。红日初升,其道大光;河出伏流,一泻汪洋。青春只有一次,谁也不应做青春的看客。中共一大召开时的13名代表平均只有28岁,而这支年轻的队伍却在风雨中迅速成长为中国人民和中华民族的主心骨。黎巴嫩的诗人纪伯伦说过,不要因为走的太远,而忘记了当初为什么出发。青年人更要扣“正”人生的第一粒扣,筑牢信仰之基,补足精神之钙,把稳思想之舵,走好人生的“每一步”。

关于学习新课标改革个人心得体会参考范文
传统的数学教学因为过分预设和封闭,使课堂教学变得机械沉闷,缺乏生气和乐趣,学生始终处于从属地位,成了教师灌输知识的容器,课堂上倦怠应付,与创造的喜悦无缘,师生都无法在课堂上焕发生命的活力。 教学过程是师生交往、积极互动、共同发展的过程,是为学而教,以学定教,互教互学,教学相长的过程。教师必须改变传统的压抑学生创造性的教学环境,通过教学模式的优化,改变教师独占课堂、学生被动接受的信息传递方式,促成师生间、学生间的多向互动和教学关系的形成。

初中生物说课稿范文《人类的起源与发展》
二、教学目标 <一>、知识目标: 1、能说出人类与现代类人猿共同起源于森林古猿。 2、知道人类是由于环境的变化,在与自然环境的艰苦斗争过程中逐渐进化来的。 3、概述人类在起源和发展过程中自身形态、使用工具等方面的变化。 <二>、能力目标: 1、通过指导学生课前收集有关人类的起源和进化的资料等,培养学生收集资料、获取信息的能力。 2、通过对人类的起源和进化的探究,打开学生思路,培养他们的观察能力、想象能力、分析能力、比较问题能力及口头表达能力。

敬老月慰问老人活动总结范文多篇
一、大力营造宣传氛围,增强居民敬老爱老意识。为了组织好我社区的“敬老月”活动,结合社区特点,开展各具特色的爱老敬老活动。 二、利用社区板报、宣传栏等各种宣传形式,大力营造爱老敬老的舆论氛围,强化了社区的爱老敬老意识。 三、开展系列敬老爱老活动,使活动落到实处。 1、20**年10月23日x商业银行x武侯支行还为xx街道各社区90岁以上老人、特困老人举办了慈善捐助活动。 2、xx街卫生服务中心免费为90岁以上老年进行体检。社区还组织健康讲座,受益人达200余人,深受老年人的欢迎。 3、社区还举办了一场大型游园活动。游园活动包括夹珠珠、套圈、扫篮球、猜谜语等项目,个个老人都乐开了怀。有100余名社区老年人参加了这此活动。 4、社区组织青年志愿者,对辖区特困、孤寡老年人进行家庭清洁、义务读报等服务,弘扬了中华民族尊老敬老的传统美德。 社区扎实开展走访慰问、志愿服务、结对帮扶等一系列敬老为老服务活动,积极为老人们办实事。做好事,提高老人的幸福指数,共享改革发展成果,让老人切实感受到关怀和温暖。开展“敬老月”活动是为了让更多的人关心老人,爱戴老人,社区一直都在弘扬尊老敬老的传统美德,通过今年的“敬老月”活动,更好的营造了关爱老年人的浓厚社会氛围。今后社区将在现有基础上继续深入开展老龄宣传活动。将尊老爱老先进事迹和先进人物即使作为典型宣传,加大尊老爱老,助老惠老的宣传力度,唤起大家尊老敬老的社会意识,为老年人实实在在地做好事,解决实际困难,充分发挥社区为老活动的实际作用。

护士个人工作报告总结范文多篇
之前常常为工作中的小事,因为不理解而情绪激动或是郁闷,但是随着时间的推移,我了解了也明白了许多:护士所做的工作就是护理患者,让患者受益,让患者满意,更要让患者尽快的康复!这就是我的工作!患者对我提出的意见那是我的不足,并不是他们无理的要求!如果连患者的需要我都没有了解到、没有及时地给予,那就是我的失职,更没有资格去谈工作的高尚了!只有患者的赞许才最高的荣誉! 在护理工作中我们应该是“做”和“说”同时进行的,甚至有些时候“说”要比“做”来得更为重要。在与病人沟通中技巧占据着很大的因素,我们科的责任护士在这方面有着很深的“功力”,让人不得不服。 从工作中使我意识到护理工作要顺利展开,首先要取得患者信任,信任是双方交往的基础,是人和人之间最美丽的语言。在交流过程中,要讲究语言的艺术性,避免套用生硬的医学术语,善于使用非语言沟通技巧,运用亲切的目光,良好的言行举止,缓和患者因紧张造成的紧张心理,使患者积极配合治疗,最后获得双羸。 “信任”是我们护士和病人之间最好的桥梁,让我们把这座桥梁搭得牢固些吧,用我们的细心,获取患者的舒心!

企业服装销售个人工作总结汇报范文3篇
一、顾客方面 我把进店的顾客分为两种: 第一种顾客,目的型的客人:逛商场怀有购物的目的,有比较明确的需求或者想法。她们可能开门见山或直奔主题索取自己喜欢的衣物,或者是半明确型的客人,是想买一件衬衫或外套,但是具体要买什么样貌还没有明确。 第二种顾客,闲逛型的顾客:此刻的商场里有太多消磨时光闲逛型的顾客,她们有的是纯粹打发时间,有的是情绪不好,到琳琅满目的商场里散心。闲逛型的顾客不必须是说不会购物,遇到她喜欢的和开心的货品时,下手也是毫不犹豫。目前商场里的顾客闲逛型的占多数,而对待闲逛型的顾客和有目的型顾客接待是不能完全相同的。闲逛型的顾客进店后,需要空间和时间来欣赏我们精心设计的漂亮陈列和货品。接待她们最忌讳的就是立刻接待,x%的时候你得到的回答是:我随便看看。显然这样的接待服务是有问题的。 二、工作方面 根据公司领导要求,做好店内的陈列及新款的展示,安排好人手更好的为公司的促销活动提升销售。定期及及时的做好竞争对手促销活动和款式变动的收集,第一时间反映到公司总部。做好会员基本资料的整理及定期跟踪,维护老客户,持续经常与老客户联系,了解客户对产品需求的动向,及时向店内的会员及老顾客反映公司的款式及店内的的优惠信息。合理的定货保证热卖及促销活动产品的库存,确保随时有货。 三、销售技巧方面 店员除了将服装展示给顾客,并加以说明之外,还要向顾客推荐服装,以引起顾客的购买的兴趣。推荐服装可运用下列方法: 首先推荐时要有信心,向顾客推荐服装时,营业员本身要有信心,才能让顾客对服装有信任感。适合于顾客的推荐。对顾客提示商品和进行说明时,应根据顾客的实际客观条件,推荐适合的服装。配合手势向顾客推荐。配合商品的特征。每类服装有不同的特征,如功能、设计、品质等方面的特征,向顾客推荐服装时,要着重强调服装的不同特征。 其次把话题集中在商品上。向顾客推荐服装时,要想方设法把话题引到服装上,同时注意观察顾客对服装的反映,以便适时地促成销售。准确地说出各类服装的优点。对顾客进行服装的说明与推荐时,要比较各类服装的不同,准确地说出各类服装的优点。

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
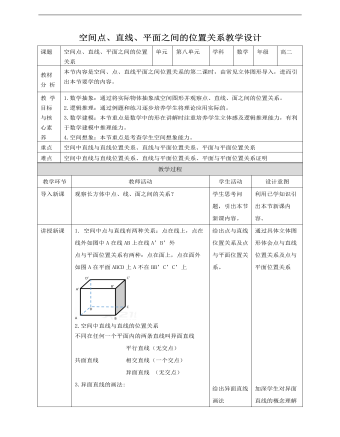
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
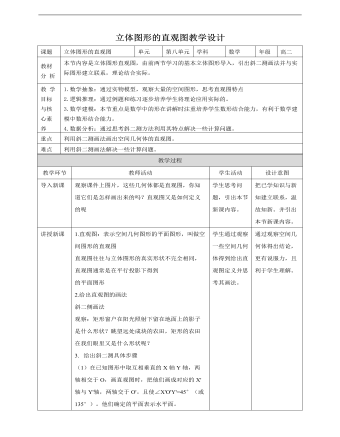
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
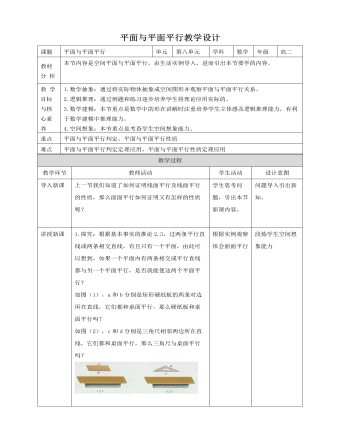
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
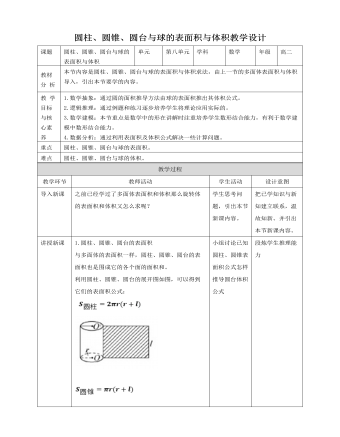
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.