-

2024年某镇在第二季度农村人居环境整治工作总结会上的讲话
人居环境整治工作既是攻坚战,也是持久战,需要我们常抓不懈、久久为功,各位要坚决克服厌战情绪和侥幸心理,牢固树立“逆水行舟,不进则退,慢进也是退”的理念,争分夺秒抓整治、全力以赴促整改,同时要保持工作韧性和连续性,杜绝“三天打鱼两天晒网”,确保长效管理不松懈、严抓共管不放松、清理彻底不反弹。同志们,人居环境整治工作既是一项民生工程,更是一项民心工程,我们既是建设者,更是受益者。希望大家回去后立即部署、迅速行动、精准发力、狠抓落实,让群众切实感受到人居环境整治的热潮,以时不我待的紧迫感、舍我其谁的使命感、造福一方的责任感推动农村人居环境整治工作再上新台阶,共同把这一事关农业农村高质量发展和群众幸福生活的大事、好事抓好抓实。

镇在2024年第二季度农村人居环境整治工作总结会上的讲话
三要继续强化督查检查,建立长效机制镇人居办要常态化开展督查检查,深入一线发现问题,做到早发现、早制止、早处置,防止小问题变成大麻烦。要明确部门责任、村(街)责任,责任到人,对思想上不重视、行动上不积极、整改上不彻底的单位和个人进行通报,对在上级考核中出现严重问题的将严肃处理。人居环境整治工作既是攻坚战,也是持久战,需要我们常抓不懈、久久为功,各位要坚决克服厌战情绪和侥幸心理,牢固树立“逆水行舟,不进则退,慢进也是退”的理念,争分夺秒抓整治、全力以赴促整改,同时要保持工作韧性和连续性,杜绝“三天打鱼两天晒网”,确保长效管理不松懈、严抓共管不放松、清理彻底不反弹。同志们,人居环境整治工作既是一项民生工程,更是一项民心工程,我们既是建设者,更是受益者。

经纪人与淘宝达人合作协议
1 甲方和手机淘宝进行战略合作,甲方负责组织淘宝达人的工作。2 乙方自身拥有良好的条件和天赋,具有成为淘宝达人的重要潜质,委托甲方扶持乙方在淘宝不断发展。双方本着自愿,平等 互惠互利,诚实信用的原则,经成分友好协商,订立如下合同条款,以资共同恪守履行:一,定义:1 淘宝达人:是指通过淘宝达人平台认证可享有淘宝达人权限的提供淘宝导购服务的推广者。2, 支付宝:第三方支付平台,公司全称为支付宝(中国)网络技术有限公司,提供网络上,转账,还款,缴费等服务,域名 alipay.com.3 推广费用:是指达人成功推广商品之后,卖家应支付的各项费用总和。推广费用=推广基数*推广费用比率(由卖家自行设置,淘宝无限制规定)。推广基数指达人推广商品被成功购买时的实际成交价格(支付宝支付金额,不包含运费及其它阿里妈妈规定不包含在内的费用)。4 阿里妈妈:指杭州阿里妈妈软件服务有限公司。

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?
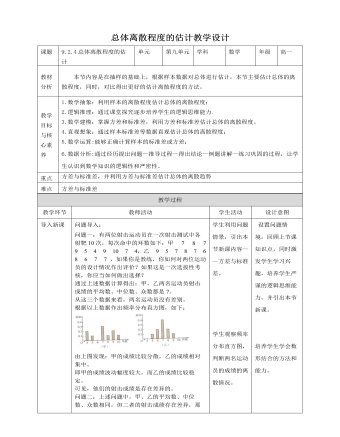
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
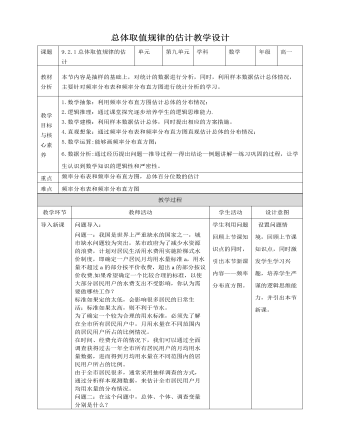
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。
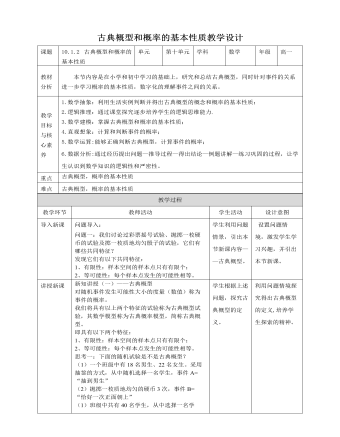
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
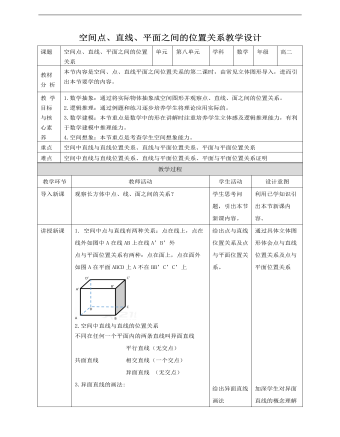
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
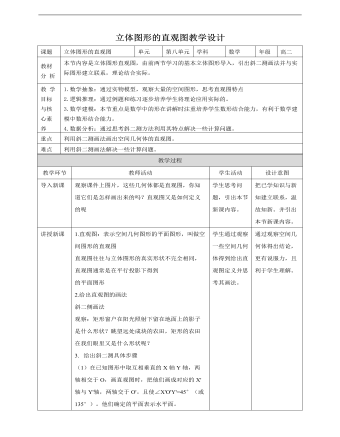
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
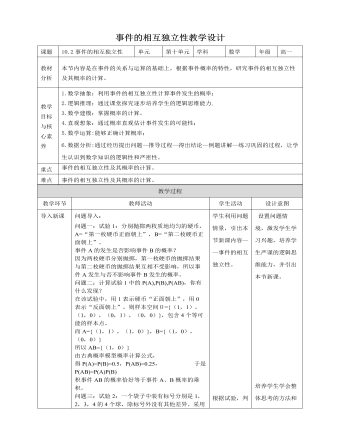
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
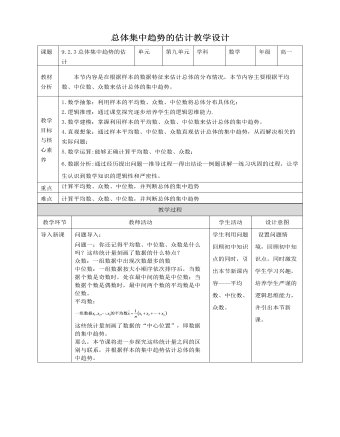
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。

国旗下的讲话:让文明与灵魂对话
演讲稿频道《国旗下的讲话:让文明与灵魂对话》,希望大家喜欢。各位老师、同学们:文明,对于许多人,是一种束缚,是被动的强迫性接受。从小,父母就教育我们如何与周围人相处,如何礼貌待人,然而,随着年龄的增长、时间的流逝,也带走了童年的纯真,长大与成熟,我们的心灵是否依然洁净?“不许随地吐痰”“不许乱丢垃圾”“禁止喧哗”“禁止吸烟”……在明确的指令下,人的外在行为因制约而沿着文明的轨迹缓慢的运行着。法国思想先驱伏尔泰论及的《被动的文明》一书就触到了人类缔造文明世界的尴尬与软肋:你看,“禁止吸烟”的标牌下不乏吞云吐雾之士,宣誓“文明公约”后仍有污言秽语之辞,校园内仍有“踏着草坪穿越广场”、“乱丢纸屑视无睹”的反文明现象。其实陋习在人类文明的历史进程中从来都不缺乏,只是在今天越来越多的知晓文明的人却在践踏文明,这怎能不引起我们深沉的反思?目光投向身边,当以作弊的方式完成《中学生日常行为规范》的考卷时;升旗仪式上面对国旗神圣庄重,事后却将国旗摇上摇下;当部分学生面对受灾的川西表现出不屑的神情时,我们,将如何去抓握文明;我们,将如何去传,承文明?

关于与节约同行国旗下讲话
与节约同行大家好!我今天的演讲题目是《与节约同行》。倡导节约反对浪费,历来是中华民族的传统美德。“历览贤国与家,成由勤俭败奢”“勤俭兴邦,奢侈覆国”、“生于忧患,死于安乐”等先贤古训流传至今。而“以艰苦奋斗为荣,以骄奢淫逸为耻”的提法则是这种美德在新时代的具体体现。今天,我们重新倡导这个传统,不仅因为其蕴含着深刻的社会现实意义,更因为它关系着我们未来的生存和发展。然而,校园中的浪费现象委实不少。每到就餐时间,食堂内的殘食桶很快就倒满了,里面堆满了只咬了几口的馒头和白花花的米饭;学校里的用电浪费现象也很普遍。

关于勤学与成才的国旗下的讲话
同学们:我们应该懂得学习对我们来说是一种需要,是我们实现理想的途径,勤学更是我们成材唯一的有效途径。任何学习意识的形成,首先应培养良好的动机,正像机器要有发动机一样,每种学习的行动的后面都有一种动力,就像发动机一样,它的功率越大,机器的动力就越大,而学习的动力越强,学习的自觉性和积极性就越高。没有这个马达,学习也就无从谈起。学习意识的形成,还需激发强烈的学习兴趣和提高“会学”的能力。“会学”能力的形成并非易事,我们知道:学习是一项艰苦的脑力劳动,任何学习成果的获得都不是朝夕可成,一蹴而就。然而有些同学终日做着“成材梦”,却不肯付诸行动去学习;羡慕那些盛开的花朵,却不用辛勤的汗水去浇灌它,空有“天生我才必有用”的想法,结果只是黄梁美梦一场空。

关于青春与理想的国旗下讲话
青春与理想尊敬的老师们,亲爱的同学们:大家好!我国旗下演讲的题目是——《青春与理想》我们撇下无知迎来了属于我们的青春。青春,让我们肆无忌惮,畅然释怀,体味风那样的自由,感受云那般的自在,因为青春赋予我们的是生命的巅峰,我们无须成熟,我们不再无知,我们唯有执着。人生是对理想的追求,理想是人生的指示灯,失去了这灯的作用,就会失去生活的勇气。因此,只有坚持远大的人生理想,才不会在生活的海洋中迷失方向。托尔斯泰将人生的理想分成:一辈子的理想,一年的理想,一个月的理想,甚至一天、一小时、一分钟的理想。同学们,当你听到这里,是否想到了自己的理想呢?

关于机遇与成才的国旗下讲话
机遇与成才同学们:大家好!我演讲的题目是《机遇与成才》在同学们中对怎样成才的问题有各种各样的说法。其中有的同学说机遇出人才,这种说法表面看来有些道理,因为许多伟人就是由于偶然的机会而走上了成功的道路,但实行上机遇不等于成功,它仅仅是一种偶然的因素。因此,机遇出人才的说法是不全面的。诚然,机遇对于人的发展有重要影响,它常常使人的一生发生转变。一个平凡而默默无闻的人,因为偶然的机会而突然发现并显示出自己都未觉察到的才能。这样的例子很多,一个著名歌星,曾经一味憧憬着外交家的生涯,但一次严重的车祸使他受到了伤痛的折磨。他后来发现最好的解说就是听音乐,没想到这竟成了他生活的转折点,他自己谱写并演唱歌曲,从此走向了成功。但是,倘若他平日没有对音乐和了解和爱好,没有这方面的才华,即使碰上这种机会也无济于事。

个人红与黑读书心得精品例文
在社会现实阻碍实现抱负时只有两种选择:退避或是反抗。那些当着小职员不求上进、整天抱怨生活乏味的青年就是退避者,他们或许平庸得舒适却被社会的前进所淘汰。能不断树立人生目标、决定实现人生理想的便是和于连有同样气概的反抗者。这个时代当然不欢迎虚伪的言行作为手段,但仍然需要对生活的热情来反抗空虚的度日。这样,于连悲剧性的结局除了昭示“个人反抗行不通”外,就有了对当今社会更实际的意义。

大班语言教案:“游戏园”与“动物园”
准备 各种人、动物活动场景图片;动物玩具。 过程 1、参观“游戏园” ①教师每次重点辅导一组小朋友,带领他们参观游戏园,其他幼儿自选活动角和游戏材料,在游戏园里开展游戏活动。 ②参观一遍后,请幼儿说说小朋友在游戏园里干什么?提示幼儿用“有的……,有的……,还有的……”句式。例如:有的小朋友在摆积木,有的小朋友在涂色、染花,还有的小朋友在看书。 ③请每个幼儿重点观察一个小朋友,然后说一说,他在干什么?他先做什么,后来又做什么?他做成了什么?或他同时在做哪几件事?提示幼儿使用“先……,然后……,最后……”;“一边……,一边……”;“又……,又……”等句式。 例如: “他在搭火车站,他先搭大楼(候车室),然后搭铁路和桥,最后建广场,他搭成了一个新火车站。”

大班数学教案:正方体与长方体
2、能在活动中培养自己的观察力以及初步的空间想象力。 3、使在探索活动中提高对认识立体图体的兴趣。 活动准备: 正方体、长方体制作材料纸若干张,正方体、长方体积木若干块。 活动过程: 1、集体活动。 观察两张制作材料,讲述异同。“小朋友看老师带来了两张纸,请你仔细观察它们有什么相同的地方和不同的地方?(相同点:都有6个图形组成。不同点:一张纸上都是一样大的正方形组成。还有一张纸上有正方形和长方形组成。) 2、幼儿操作活动。 “今天老师就要请小朋友用这两张纸来变魔术,怎么做呢?” (1)介绍制作形体的方法。 出示示意图,教师简单讲述制作方法。

