-

北师大初中九年级数学下册切线的判定及三角形的内切圆教案
解析:(1)连接BI,根据I是△ABC的内心,得出∠1=∠2,∠3=∠4,再根据∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,得出∠BIE=∠IBE,即可证出IE=BE;(2)由三角形的内心,得到角平分线,根据等腰三角形的性质得到边相等,由等量代换得到四条边都相等,推出四边形是菱形.解:(1)BE=IE.理由如下:如图①,连接BI,∵I是△ABC的内心,∴∠1=∠2,∠3=∠4.∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,∴∠BIE=∠IBE,∴BE=IE;(2)四边形BECI是菱形.证明如下:∵∠BED=∠CED=60°,∴∠ABC=∠ACB=60°,∴BE=CE.∵I是△ABC的内心,∴∠4=12∠ABC=30°,∠ICD=12∠ACB=30°,∴∠4=∠ICD,∴BI=IC.由(1)证得IE=BE,∴BE=CE=BI=IC,∴四边形BECI是菱形.方法总结:解决本题要掌握三角形的内心的性质,以及圆周角定理.

北师大初中九年级数学下册直线和圆的位置关系及切线的性质教案
解析:(1)由切线的性质得AB⊥BF,因为CD⊥AB,所以CD∥BF,由平行线的性质得∠ADC=∠F,由圆周角定理的推论得∠ABC=∠ADC,于是证得∠ABC=∠F;(2)连接BD.由直径所对的圆周角是直角得∠ADB=90°,因为∠ABF=90°,然后运用解直角三角形解答.(1)证明:∵BF为⊙O的切线,∴AB⊥BF.∵CD⊥AB,∴∠ABF=∠AHD=90°,∴CD∥BF.∴∠ADC=∠F.又∵∠ABC=∠ADC,∴∠ABC=∠F;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°.由(1)可知∠ABF=90°,∴∠ABD+∠DBF=90°,∴∠A=∠DBF.又∵∠A=∠C,∴∠C=∠DBF.在Rt△DBF中,sin∠DBF=sinC=35,DF=6,∴BF=10,∴BD=8.在Rt△ABD中,sinA=sinC=35,BD=8,∴AB=403.∴⊙O的半径为203.方法总结:运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

人音版小学音乐五年级上册堆雪人说课稿
第二首是中国歌曲《龙咚锵》,欣赏后师生共同讨论下我国过年的习俗,然后在《堆雪人》伴奏的背景音乐下,观看中国过年时的各种场景【白板播放歌曲拖拉图片】这部分环节的设计是让学生初步感受不同地域的音乐风格和音乐所表达的“过新年”热闹氛围,了解过年的风俗,在音乐学习中受到节日文化的熏陶,感受音乐与生活、与自然的关系。最后播放《堆雪人》视频,【白板播放歌曲视频】学生在《堆雪人》的音乐声中,在亲身制作的贺年卡上,贴上雪花窗花贴纸,作为新年的礼物送给父母。感恩父母感受生活的幸福,同时《堆雪人》这首歌曲的旋律也贯穿了整节音乐课。本次是我把电子白板运用到音乐教学中的初次尝试,在制作与操作的过程中明显还不够熟练,有待提高。请在座的各位领导老师们多提宝贵意见,谢谢大家。

人音版小学音乐五年级上册清晨说课稿
让学生自主的用各种自己喜欢的打击乐器来拍打节奏,感受节奏的活泼欢快。(节奏示范)通过让同学们自选自己喜欢的打击乐器来拍打节奏可以激发学生们对节奏学习的积极性,从而让枯燥的节奏练习变的更加生动,我还会给学生分组并合作拍打节奏。感受不同的打击乐器给节奏增添的色彩。(3)歌曲的优美在学生能够完整的哼唱旋律和拍打节奏之后,我会引导学生自主的将旋律和歌词相结合的演唱出来,我谈伴奏。(完整歌曲示范)通过三遍又慢到快的练习,学生基本能够完整的演唱歌曲。在三遍的练习过程中学生可以明显感受到自己在歌唱方面的进步。从而更好地激发学生的歌唱兴趣以及自主学习歌唱的能力。这首曲子的歌唱顺序是需要学生特别注意的,其中有反复记号D.C. 我会带领学生一起学习这个反复记号的意思是从头反复到Fine处结束。在学生掌握反复记号之后,再次带领学生以正确的演唱顺序来进行歌曲的演唱。

人音版小学音乐五年级上册渔舟唱晚说课稿
5、好多同学听到了一些声音,大家再认真听一遍,看还能听出什么声音来。[这个环节是本课重点,刚开始老师引导听,为了不让学生感到枯燥,我特别找了渔舟唱晚的影像资料,结合乐曲欣赏,也能让学生更直观的认知乐曲。最后的复听让学生在主题变换处给老师作出提示手势,增加了互动,也能让学生更好地掌握这首乐曲的结构。](五)拓展延伸 (约6分钟)1、简单介绍民族乐曲在国际上的影响,使学生对民族音乐有自豪感觉,培养学生热爱民族音乐,热爱祖国文化。同学们给的主题提示非常到位,说明我们已经抓住了乐曲的灵魂。《渔舟唱晚》是我国民族音乐殿堂中一颗璀璨的明珠,中国对外文化协会将此曲作为我国民族音乐的代表之一送给国际友人。我国的民族广播乐团在国外演出时,《渔舟唱晚》经常作为重要乐曲演出,并获得国际友人很高的评价。

人音版小学音乐五年级上册雨花石说课稿
播放音乐《雨花石》并请学生生观看一些有关石头的图片教师有感情的范唱。教唱歌谱。在教唱歌谱中注意难点的解决,分别出示以小石头造型的节奏卡片,复习四分音符、八分音符及四分休止符。还有新学的音符,十六分休止符。学生根据直观判断时植的长短,并口读,练习。有感情的读歌词听琴声轻声哼唱歌曲。其中请学生体会与比较:运用休止符的地方你有什么样的感受?如果不用会怎样。唱一唱,比一比,说一说。请学生有感情的演唱,教师及时给予鼓励。教师总结石头可贵的精神。石头虽小,却有很多的作用等我们去发现。法国著名艺术家罗丹曾说过:“对于我们的眼睛,不是缺少美,而是缺少发现。”我想,通过这样的教学设计,让学生在音乐中认识美,在生活中寻找美,在未来里创造美,让美融入每一个孩子以上设计肯定还有一些不足之处,敬请各位老师提出宝贵意见。

人音版小学音乐五年级上册苹果丰收说课稿
通过这种方法,一步一步,由浅入深的让学生感受、体验、表现,在增加喜庆气氛的同时感受朝鲜舞的特点,进而使学生对朝鲜族的音乐风格有了一定的了解。《苹果丰收》歌曲速度很快,能够轻松地咬字、吐字,清晰的表达歌曲内容是本课的另一个重点。因此,我重新录制了音乐,学习的过程中我随时根据学生的学习情况改变音乐的速度,在歌曲学会后再逐渐加快速度,这样使学生学起来轻松了许多。然后,我又以歌中的一句为例,让学生看着又红又大的苹果做吃苹果时的样子和甜滋滋的表情,让学生就带着这样的感受来唱“一个个苹果惹人爱,惹呀么惹人爱”一句,我在此处进行声音和情感的处理,达到满意后再延伸到整首歌曲,最后达到从音乐中体验苹果丰收带来的快乐,用热情饱满的情绪、流畅的演唱歌曲,表现朝鲜族人民喜获苹果丰收时的喜悦之情的教学目标。本课教学设计之不足之处,将在进一步的教学实践中改进。

人音版小学音乐五年级上册雏鹰之歌说课稿
5找出下滑音记号 6复唱歌谱 7 教唱歌曲 8分析歌曲 9歌曲结尾重点唱 10跟随伴奏完整唱一遍 11变换演唱方式 12请学生有感情的演唱, 教师及时给予鼓励. (三).知识拓展 1、导言 进入了21世纪不少作曲谱写了很多少年儿童立志歌曲,其中在512汶川大地震英雄少年表彰晚会上会上的创作的歌曲《英雄少年》最为激人奋进 2、聆听《英雄少年》 课堂小结: 通过这节课的学习,希望同学们要像歌里唱的 一样要做勇敢的雄鹰,不畏风雨,勇往直前(四)歌声中结束: 本课的设计,力求体现以人为本的思想,着眼于学生的主动发展,通过充分的音乐实践培养学生的能力,提高音乐素养。多媒体的教学手段,为课堂带来了活力,注入了生机,弥补了教学中单一的教学方法,给了学生以直观的美感享受。

人音版小学音乐五年级上册晚风说课稿
在这一环节里我设计了让学生们利用高位置的声音轻声朗诵歌词,来理解歌词内容及其主题思想,便于他们在演唱时把握感情表达的分寸。 第六环节是拓展部分,主要是让学生们在《晚风》的旋律中了解一些有关俄罗斯的人土风情,拓展学生的视野。其实对唱好合唱来说,有一个好的“音乐的耳朵”是非常重要的。合唱讲究的是一个整体的合作,只有相互地倾听,求得准确和谐,才能保证合唱的成功。同时合唱时的音准务求准确,这样才能在大家的努力下,共同创造出优美动听的和声,所以每个人对自己所发出的声音,要做到“心”里有数,而这种感觉的建立,有很大一部分依赖于“音乐的耳朵”,要唱得好,首先要听得好。在平时的课堂教学中,要让学生多听,听录音、听教师范唱、听琴弹奏、听学生唱,在多听中培养自己音乐的耳朵。

人音版小学音乐五年级上册丰收锣鼓说课稿
(3)播放第三部分。重点引导学生从笛子和云锣的演奏中展开丰富想象. 帮助学生养成从“音乐”的角度分析作品的习惯。(4)第四部分的聆听由于与第一部分较为相似,我主要通过音乐速度的变化启发学生感受音乐的变化。3、完整复听 拓展延伸为了使学生对乐曲对民族管弦乐队有更深入的印象,我借助录象,请学生边听边看,并牵引出民族管弦乐队的演出空间布局。随后要求学生即兴对照画面,把全班分为四组按照四种民族乐器分类模仿管弦乐队演出样式,随《丰收锣鼓》音乐徒手演奏。不仅能有效激发孩子对民族音乐的兴趣,同时也进一步复习巩固了民族乐器的四个分类。把音乐课堂推向了高潮。最后一个环节就是小结部分,请学生回去后搜集相关的民乐资料,使学生通过本课的学习更加关注民族音乐。

人音版小学音乐五年级上册外婆的澎湖湾说课稿
㈢拓展(十分钟)利用打击乐器为歌曲B部分伴奏:这一部分在学生能完整并且熟练演唱全曲后,为了丰富这首曲的音乐色彩,我会引导学生小组合作利用简单的打击乐器为歌曲的B部分配上伴奏,并请学生分成三个组,分别为三角铁组、沙锤组、伴唱组。这里我会看学生的反应,如果学生有较强的节奏感,那我就会让他们自己自由的为歌曲编配伴奏,如果这方面弱一点,我就会给他们指定伴奏节奏,通过练习再为歌曲伴奏,伴唱组设计自己的声势节奏,等三角铁组和沙锤组熟练掌握伴奏节奏后,请演唱组边演唱B部分边拍声势节奏,并加入三角铁和沙锤组的伴奏。最后,完整演唱全曲,A部分请全体学生随音乐边唱边律动,B部分加入打击乐器伴奏,我会弹着钢琴加入完成这一次的师生合作演出。

人音版小学音乐五年级上册雪花带来冬天的梦说课稿
(三)实践操作,表现歌曲。课标中指出,“表现是实践性很强的音乐学习领域,是学习音乐的基础性内容,是培养学生音乐表现能力和审美能力的重要途径。”再加上对于这个年龄段的学生来讲,他们特别喜欢表现自己,所以,我充分发挥集体的力量,设计“小小音乐家”的教学环节,让同学们在小组中合作学习,采用不同形式演唱、用打击乐器伴奏、歌舞表演等形式将唱、奏结合,唱、演结合,巩固学生对歌曲的学习,体验合作学习的快乐,养成学生共同参与的群体意识和相互尊重的合作精神和实践能力,这也更体现了课标中音乐课程价值所提出的要培养学生的“社会交往价值”。(四)拓展延伸,创编歌曲。课标中的“文化传承价值”中明确提出:“要让孩子们通过学习世界上其他国家和民族的的音乐文化,拓宽他们的审美视野,认识世界各民族音乐文化的丰富性和多样性,增进对不同文化的理解、尊重和热爱。”

人教版新课标小学数学二年级上册两位数加两位数(进位加) 说课稿2篇
一、说教材:本课时主要的内容就是让学生在情境中掌握两位数加两位数的进位加法计算,让学生通过尝试和探索出多种算法,体验多种算法,然后比较出最好的算法。教学目标:1、通过具体的情境使学生更一步的理解加法的意义和提高学生的估算意识。2、通过学生的合作学习从而能探讨出多种计算两位数减两位退位减法的方法。3、培养学生的数学口语表达能力,提高学生的学习兴趣。4、掌握两位数加两位数(进位加)竖式的写法。重点:(1)通过学生的合作学习从而能探讨出多种计算两位数减两位退位减法的方法。(2)掌握笔算加法的计算法则。难点:对多样化算法进行优化,达到正确完成计算。发展学生的估算意识、和探究意识和解决实际问题的能力。二、说教法:组织学生在前面计算的基础上,自主探索出两位数加两位(进位加)的计算方法,并通过交流、讨论,达到对算法的优化,在通过“试一试”、“算一算”、“想一想”等形式达到知识的掌握。

人教版新课标小学数学二年级上册两位数加两位数(不进位加) 说课稿
今天我说课的内容是二年级上册第二单元《100以内的加法和减法》的第一课时,两位数加两位数的不进位加法。教材通过参观博物馆的情境图引出两位数的不进位和进位加法。本节课主要解决不进位加法竖式计算中的对位和计算顺序问题。由于本节课是在学生已经掌握两位数加整十数、两位数加一位数的基础上学习的内容,这堂课的关键是引导学生运用这些已有的知识经验,借助位值图,通过自己的操作探究、合作学习,将新知识转化、纳入已有的认知结构,自主地学习两位数加两位数不进位加法的计算方法。因此本节课的目标确定为:知识与能力:1、充分利用直观手段,帮助学生理解和掌握笔算两位数加两位数的方法。2、培养学生观察、分析、解决问题的能力。过程与方法:运用直观手段,创设有意义的问题情境和游戏活动来组织教学,让学生通过动手操作、自主探索、合作交流等方法掌握算法,提高学习积极性,增强学习数学的兴趣。

人教版新课标小学数学二年级上册两位数减两位数(不退位减)说课稿2篇
说教材:(1)教学内容:人民教育出版社出版的九年义务教育六年制小学数学教科书第三册中的第16—17页的例1及“做一做”,练习三1、2、3、4、题。(2)教材分析(教材的前后联系,地位作用及编排意图):两位数减两位数是学生学习笔算减法的开始,也是以后学习多位笔算减法的基础。由于笔算减法是在口算减法的基础上进行教学的,所以教材先安排了口算整十数减整十数、两位数减整十数、两位数减一位数的复习,为理解笔算做好准备。教材由两位数减一位数的不退位减法口算引出两位数减一位数的不退位减法的笔算。说明这种口算题也可以写成竖式,用笔算。然后,对照直观图说明计算时要把相同数位对齐,从个位减起的计算顺序。(3)教学目标:根据教材的编排意图以及学生的实际,我确定本课的教学目标是:使学生理解笔算两位数减两位数的算理,掌握竖式的写法和计算方法,并能正确的笔算。培养学生知识迁移的能力和口头表达能力,培养学生仔细计算的良好学习习惯。

人教版新课标小学数学二年级上册两位数减两位数(退位减)说课稿2篇
一、说教材1、教学内容本节课是义务教育课程标准实验教材人教版小学数学第三册18至19页的内容。它是在学生学习了20以内的退位减法、两位数减一位数和两位数减整十数以及两位数减两位数的不退位减法笔算的基础上学习的。它是以后学习多位数减法的重要基础。2、教学目标(1)、知识目标:使学生在理解算理的基础上初步掌握两位数退位减法的计算方法,并能正确的进行计算。(2)、技能目标:培养学生的动手操作能力,发展学生的思维和语言表达能力。(3)、情感目标:通过情景的创设,培养学生的爱国之情,同时让学生在自主探索算法的基础上体验到成功的喜悦。3、教学重点:本节课的重点是理解笔算两位数退位减的算理,能正确用竖式计算。4、教学难点:理解两位数减两位数退位减法的算理。
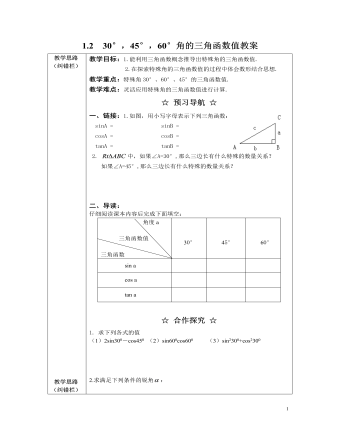
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示

北师大初中九年级数学下册确定二次函数的表达式1教案
解析:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,根据对称轴是x=-3,求出b=6,即可得出答案;(2)根据CD∥x轴,得出点C与点D关于x=-3对称,根据点C在对称轴左侧,且CD=8,求出点C的横坐标和纵坐标,再根据点B的坐标为(0,5),求出△BCD中CD边上的高,即可求出△BCD的面积.解:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,∴c-4b=-19.∵对称轴是x=-3,∴-b2=-3,∴b=6,∴c=5,∴抛物线的解析式是y=x2+6x+5;(2)∵CD∥x轴,∴点C与点D关于x=-3对称.∵点C在对称轴左侧,且CD=8,∴点C的横坐标为-7,∴点C的纵坐标为(-7)2+6×(-7)+5=12.∵点B的坐标为(0,5),∴△BCD中CD边上的高为12-5=7,∴△BCD的面积=12×8×7=28.方法总结:此题考查了待定系数法求二次函数的解析式以及二次函数的图象和性质,注意掌握数形结合思想与方程思想的应用.

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.