-

人教版高中地理选修1第二章第二节月球和地月系教案
我们将三球仪中的月球放在地球和太阳之间时,对照“月相成因图”,它的暗面完全对着地球,而被太阳照亮的一面正对着太阳,我们看不到月亮,这时正是农历初一,被称为“新月”。又称为“朔”。 过了新月,月亮被照亮的部分慢慢地转向地球。当它从太阳的光辉中出现时,便出现了一丝蛾眉的弯月,此时为农历的初三、初四,因其形似蛾眉,被称为“蛾眉月”。此后,被太阳光照亮的部分越来越多地转向地球,当有一半亮面和一半暗面都对着地球时,明亮部分和黑暗部分的界线似乎像一张弓中没有拉动的弦。此时是夏历初七、初八,称为“上弦月”。这时月亮很明亮,有时在白天也能看见。在往后,月亮明亮部分越来越增大,当它转到与新月正好相反时,被太阳照亮的部分全都对着地球,看起来月亮就似一轮圆月,此时正是 农历十五、十六、十七,称为“满月”,又称为“望”。

人教版高中地理选修1地球的早期演化和地质年代教案
学习方法实验法、讨论法。教学 媒体投影仪、投影片、岩石标本、实验器具。学习过程一、地球的早期演化和地质年代1、思考回答:初生地球 有什么特点?2、【启发提问】看课本大气的早期是怎样演化的?水圈是怎样形成? 学生分组讨论后回答,相互启发补充。3、学生讨论、回答:生命起源的过程怎样?大气又是怎样继续演化的?二、记录地球历史 的“书页 ”——岩层和化石1、学生讨论 、回答:地球上岩浆岩、变质岩、沉积岩三种岩石的形成和特点2 5、【启发提问】化石是怎样形成的?他有什么作用?三、地质年代1、【启发提问】地质年代划分依据是什么?2、学生讨论、总结。各阶段的特点?学后记:

人教版高中地理选修1第二章第三节月相和潮汐教案
创设情境、激发兴趣(5分钟)教师:(锁住屏幕)月相变化与我们人类关系十 分密切。美国著名总统林肯在年轻时担任律师期间曾利用月相变化规律,为当事人进行了成功的辩护,赢得了人们的尊重。月相变化是怎样变化的?月相变化有什么规律,这就是我们今天学习内容。(边演示 学习软件边介绍)我们今天学习主要有三个任务,其中学习任务一要注意在空格中填写农历日期,不认识有关月相的请参照下面的相关学习软件。 完成学习任务二时要注意运用学习软件,首先点击月相,观察日地与月地连线的关系,再观察月亮出没时间现太阳的关系。如满月时,日地与月地连线成1800夹角,当太阳从东方升起时,月亮从西方落下(6时);当太阳从西方落下时,月亮从东方升起 (18时)。满月可见时间是18时到第二天6时。学习任务三请你先判 断图中月相是否正确,如果不正确,请把你认为正确的月相拖到图中适当位置。下面请你们开始学习。

人教版高中地理选修1第一章第一节天体和天体系统教案
【概括】天体是在不断的运动着的。运动着的天体互相吸引和互相绕转,从而形成天体系统。【板书】四、天体系统【启发】天体系统有大有小,大的天体系统又可包含许多小的天体系统。刚才同学们提到的三个天体系统之间是如何包含的呢?(银河系含太阳系,太阳系含地月系)【挂图讲解】地月系只有两个天体,地球和月球,它们之间的平均距离为384401千米;太阳系则包括太阳、九大行星、数十颗卫星及其它天体,整个太阳系的直径至少100亿千米以上;而银河系则拥有2000多亿颗太阳恒星及恒星系统,包括了我 们用肉眼能看到的所有恒星,其主体部分的直径达7万光年,太阳就处于距银河系中心2.3万光年的位置上。【讲解】银河系已如此庞大,是否 就是最大的天体系统呢?是否就是我们的宇宙呢?还远远不是。利用天文望远镜,我们可以观测到在银河系之外,还有约10亿个类似的天体系统,它们被统称为河外星系。

人教版高中地理选修2浦东新区的规划和开发教案
1、图12.5“浦东新区的规划图”首先了解浦东新区的位置,浦东新区位于黄浦江东部,东临东海,北濒长江,面积广阔,地形平坦,和上海市繁华的外滩和南京路只有一江之隔;其次要了解城市规划的功能分区。2、图12.6“浦东新区图”图中可见已建成陆家嘴、张江、金桥、外高桥、孙桥等功能分区,理解浦东作为现代化城市新区的格局已基本形成。3、图12.8“浦东新区的产业结构图(1997年)”读此图应该明确,浦东新区国民经济的主要支柱是工业,第二产业占62.1%,比重最小的是第一产业,仅占0.8%,为充分发挥浦东新区的龙头作用,今后该区应继续把第二产业放在首要位置,成为上海市高新技术产业和现代工业的基地。【教学内容】一、浦东新区的开发条件和作用建设城市新区是上海市发展的必然选择,建设新城区首先要选择合适的区域。

人教版高中地理选修1恒星的一生和宇宙的演化教案
①演示动画,理解大爆炸宇宙论②主要观点:? 大约150亿年前,我们所处的宇宙全部以粒子的形式、极高的温度、极大的密度,被挤压在一个“原始火球”中。? 大爆炸使物质四散出击,宇宙空间不断膨胀,温度也相应下降,后来相继出现在宇宙中的所有星系、恒星、行星乃至生命。2、其它宇宙形成理¬——稳定理论3、大胆猜测:宇宙的将来史蒂芬·霍金是英国物理学家,他提出的黑洞理论和宇宙无边界的设想成了现代宇宙学的重要基石。霍金的宇宙无边界的设想是这样的:第一,宇宙是无边的。第二,宇宙不是一个可以任意赋予初始条件或边界的一般系统。霍金预言宇宙有两种结局:永远膨胀下去,不断地扩大,我们将看到所有星系的星球老化、死亡,剩下我们孤零零的,在一片黑暗当中。或者会塌缩而在大挤压处终结科学巨人霍金:探索的精神)

人教版高中地理选修2长江三峡工程建设的意义和作用教案
1、图5.3“长江中游防洪形势图”(1)读图后,说出长江中游的主要水文特征:多曲流、多支流、多湖泊。(2)分析“千里长江,险在荆江”的原因及其解决的措施:荆江河段特别弯曲,有“九曲回肠”之称,水流不畅,泥沙大量淤积,使河床高出两岸平地,形成“悬河”。一旦发生洪水,堤防漫溃直接威胁江汉平原和洞庭湖区的农田、企业、城市、交通要道和人民生命财产安全。新中国成立后,治理荆江的措施主要有:修建荆江分洪工程,完成了几处裁弯取直工程,加固了荆江大堤。(3)在图上找出主要分洪区。2、图5.5“长江三峡图”(1)掌握长江三峡的组成、名称及其在图上的位置:说明:①长江三峡的长度数据有多种,如192千米、193千米、204千米208千米等。②有的著作中把大宁河宽谷划入瞿塘峡,把香溪宽谷划入西陵峡。

人教A版高中数学必修一对数函数的图像和性质教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.2节《对数函数的图像和性质》 是高中数学在指数函数之后的重要初等函数之一。对数函数与指数函数联系密切,无论是研究的思想方法方法还是图像及性质,都有其共通之处。相较于指数函数,对数函数的图象亦有其独特的美感。在类比推理的过程中,感受图像的变化,认识变化的规律,这是提高学生直观想象能力的一个重要的过程。为之后学习数学提供了更多角度的分析方法。培养和发展学生逻辑推理、数学直观、数学抽象、和数学建模的核心素养。1、掌握对数函数的图像和性质;能利用对数函数的图像与性质来解决简单问题;2、经过探究对数函数的图像和性质,对数函数与指数函数图像之间的联系,对数函数内部的的联系。培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;渗透类比等基本数学思想方法。
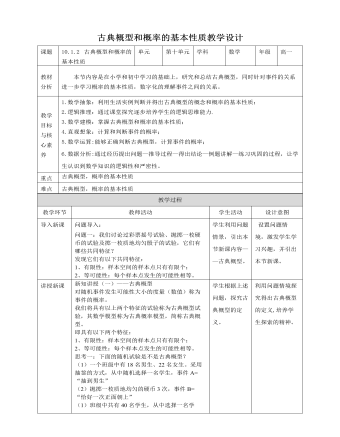
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
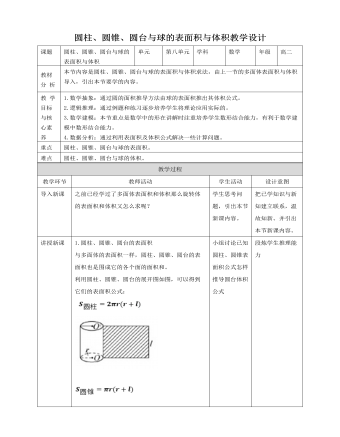
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.

人教版高中数学选择性必修二等差数列的前n项和公式(1)教学设计
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献. 问题1:为什么1+100=2+99=…=50+51呢?这是巧合吗?试从数列角度给出解释.高斯的算法:(1+100)+(2+99)+…+(50+51)= 101×50=5050高斯的算法实际上解决了求等差数列:1,2,3,…,n,"… " 前100项的和问题.等差数列中,下标和相等的两项和相等.设 an=n,则 a1=1,a2=2,a3=3,…如果数列{an} 是等差数列,p,q,s,t∈N*,且 p+q=s+t,则 ap+aq=as+at 可得:a_1+a_100=a_2+a_99=?=a_50+a_51问题2: 你能用上述方法计算1+2+3+… +101吗?问题3: 你能计算1+2+3+… +n吗?需要对项数的奇偶进行分类讨论.当n为偶数时, S_n=(1+n)+[(2+(n-1)]+?+[(n/2+(n/2-1)]=(1+n)+(1+n)…+(1+n)=n/2 (1+n) =(n(1+n))/2当n为奇数数时, n-1为偶数

人教版高中数学选择性必修二等比数列的前n项和公式 (1) 教学设计
新知探究国际象棋起源于古代印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦粒的质量为40克,据查,2016--2017年度世界年度小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.问题1:每个格子里放的麦粒数可以构成一个数列,请判断分析这个数列是否是等比数列?并写出这个等比数列的通项公式.是等比数列,首项是1,公比是2,共64项. 通项公式为〖a_n=2〗^(n-1)问题2:请将发明者的要求表述成数学问题.

人教版高中数学选择性必修二等比数列的前n项和公式 (2) 教学设计
二、典例解析例10. 如图,正方形ABCD 的边长为5cm ,取正方形ABCD 各边的中点E,F,G,H, 作第2个正方形 EFGH,然后再取正方形EFGH各边的中点I,J,K,L,作第3个正方形IJKL ,依此方法一直继续下去. (1) 求从正方形ABCD 开始,连续10个正方形的面积之和;(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?分析:可以利用数列表示各正方形的面积,根据条件可知,这是一个等比数列。解:设正方形的面积为a_1,后续各正方形的面积依次为a_2, a_(3, ) 〖…,a〗_n,…,则a_1=25,由于第k+1个正方形的顶点分别是第k个正方形各边的中点,所以a_(k+1)=〖1/2 a〗_k,因此{a_n},是以25为首项,1/2为公比的等比数列.设{a_n}的前项和为S_n(1)S_10=(25×[1-(1/2)^10 ] )/("1 " -1/2)=50×[1-(1/2)^10 ]=25575/512所以,前10个正方形的面积之和为25575/512cm^2.(2)当无限增大时,无限趋近于所有正方形的面积和

人教版高中数学选择性必修二等差数列的前n项和公式(2)教学设计
课前小测1.思考辨析(1)若Sn为等差数列{an}的前n项和,则数列Snn也是等差数列.( )(2)若a1>0,d<0,则等差数列中所有正项之和最大.( )(3)在等差数列中,Sn是其前n项和,则有S2n-1=(2n-1)an.( )[答案] (1)√ (2)√ (3)√2.在项数为2n+1的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则n等于( )A.9 B.10 C.11 D.12B [∵S奇S偶=n+1n,∴165150=n+1n.∴n=10.故选B项.]3.等差数列{an}中,S2=4,S4=9,则S6=________.15 [由S2,S4-S2,S6-S4成等差数列得2(S4-S2)=S2+(S6-S4)解得S6=15.]4.已知数列{an}的通项公式是an=2n-48,则Sn取得最小值时,n为________.23或24 [由an≤0即2n-48≤0得n≤24.∴所有负项的和最小,即n=23或24.]二、典例解析例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?分析:将第1排到第20排的座位数依次排成一列,构成数列{an} ,设数列{an} 的前n项和为S_n。

镇社会保障服务中心2023年工作总结和2024年重点工作任务
(二)城乡居民医疗保险工作。一是严格执行政策,采取有效措施,不折不扣的完成好2024年的征缴工作目标任务。二是做好城乡居民零星报销及系统信息维护等常规工作。三是搞好城乡居民医疗保险工作的来信来访,收集并及时向上级反映医疗保险中出现的新情况,配合上级医保部门做好医疗保险的调研工作,始终贯彻以人为本的原则,树立全心全意为人民服务的宗旨,做好做活服务,提升服务质量,创新服务模式,不仅使群众成为参加医疗保险的主体,更是真正的受益者,把我们的工作做到程序便捷化,创建文明服务窗口,真正使医疗保险工作达到政府得民心,群众得实惠,医保工作得发展的工作目标。(三)便民服务中心管理工作。一是加强自身建设,进一步健全、完善各项管理制度,加强效能监督管理,加强对中心工作人员的考核制度的建立。二是依法行政,规范运行。

政务服务中心2024年上半年工作总结和下半年工作打算的报告
(二)持续提升网办能力。全面推行政务服务事项“网上可办”“全程网办”“掌上办”“指尖办”“自助办”。狠抓落实“一网通办”各项数据指标提升工作,努力保持“一网通办”工作成绩在全市第一梯队。(三)推进综窗改革。严格按照“应进必进”原则,完成14个部门集中进驻并授权到位,已进驻部门完成自查“明进暗不进”,确保事项全部进驻并授权到位;同步推动“一窗受理”到位,7月底前,“分领域专区综合窗口”逐步推动业务整合,科学整合压缩窗口,削减行政成本,全面实施“集成服务”。“无差别综合窗口”根据我县实际情况,推进落实综窗接件人员到位,完成除9个分领域外的其它所有事项整合进驻无差别综窗,由政务服务中心综窗接件、统一推送、内部流转至部门审批、再综窗出件,扭转办件量少的部门也需派驻人员的财政经费浪费,实现效率集成、成本压缩。

XX市公共资源交易中心2024年上半年工作总结和下半年工作谋划
(四)强化新技术应用。持续推进大数据分析等新技术在公共资源交易领域的应用,依靠科技创新破解公共资源交易发展中遇到的重大问题和突出矛盾。持续探索“大数据分析系统”“智能电子档案归集系统”“监控视频自动刻录系统”“手机移动端系统”等功能模块建设,推进公共资源交易由“电子交易”向“智慧交易”升级。持续完善不见面、远程异地评标系统建设,不断提升全市公共资源交易电子化水平。(五)加强公共资源交易智慧大数据分析平台在招标投标领域的运用。启用市公共资源交易智慧大数据分析平台,建立公共资源交易数据模型,强化数据融通和价值挖掘,提升交易中心围标串标风险预警及监测能力。(六)加强系统安全防护。开展系统、机房网络的安全检测,在原有平台系统定期维护更新的基础上,全面优化升级信息系统的上云方案,不断满足全市公共资源电子系统安全建设要求。

2024年区公共资源交易中心上半年工作总结和下半年工作计划
一是强化服务理念,创新服务方式,深化作风建设,提高工作效能,进一步增强大局意识、责任意识和服务意识。坚持以优质服务、高效服务为工作标准,以熟练的业务技能、热情的服务态度、规范的服务行为、公正的办事作风和最大的社会效益,树立诚实守信的社会形象,打造优质高效的服务品牌。二是进一步落实交易项目的提前介入、主动服务工作机制,提前、主动与招标人联系,提供政策咨询、程序引导、业务指导等服务,帮助解决招标和采购中遇到的一些困难和问题。(三)坚持奋发进取,突出创新创优,不断创新公共资源交易中心工作。一是积极与上级相关行业主管单位沟通协调,加强投标人交易行为监管,维护公共资源交易市场秩序。二是密切与纪检监察等有关职能部门的沟通联系,加强项目进场交易情况督查,加强对交易各环节监管,及时纠正交易过程中存在的问题,不断提升交易服务水平,努力实现阳光交易。

xx市第一高级中学2024年上半年工作总结和下半年工作计划
(一)完成校本部和莲溪校区的招生计划。暑假期间,充分利用微信公众号、微信朋友圈、视频号、抖音等各类宣传媒介,对招生进行宣传报道,营造良好的舆论氛围。开放咨询渠道,严格按照招生方案进行招生,确保圆满完成招生计划。(二)继续招纳贤才,进一步充实教师队伍。下半年将继续协助人社局、教体局开展校园招聘和社会招聘,广纳贤才,为学校的可持续发展菱定基础。(三)持续规范教学常规,提高教育教学质量一是抓好教学常规,教学常规的中心环节在课堂,力求课堂效果最大化。二是扎实做好尖子生培养工作。在尖子生培养方面,做到“精心”、“精品”,致力于寻求尖子生培养的良方。

某区公共资源交易中心2024年上半年工作总结和下半年工作计划
(二)提高服务意识,创新服务方式,树立公共资源交易平台良好形象。一是强化服务理念,创新服务方式,深化作风建设,提高工作效能,进一步增强大局意识、责任意识和服务意识。坚持以优质服务、高效服务为工作标准,以熟练的业务技能、热情的服务态度、规范的服务行为、公正的办事作风和最大的社会效益,树立诚实守信的社会形象,打造优质高效的服务品牌。二是进一步落实交易项目的提前介入、主动服务工作机制,提前、主动与招标人联系,提供政策咨询、程序引导、业务指导等服务,帮助解决招标和采购中遇到的一些困难和问题。(三)坚持奋发进取,突出创新创优,不断创新公共资源交易中心工作。一是积极与上级相关行业主管单位沟通协调,加强投标人交易行为监管,维护公共资源交易市场秩序。二是密切与纪检监察等有关职能部门的沟通联系,加强项目进场交易情况督查,加强对交易各环节监管,及时纠正交易过程中存在的问题,不断提升交易服务水平,努力实现阳光交易。





