-

点到直线的距离公式教学设计人教A版高中数学选择性必修第一册
4.已知△ABC三个顶点坐标A(-1,3),B(-3,0),C(1,2),求△ABC的面积S.【解析】由直线方程的两点式得直线BC的方程为 = ,即x-2y+3=0,由两点间距离公式得|BC|= ,点A到BC的距离为d,即为BC边上的高,d= ,所以S= |BC|·d= ×2 × =4,即△ABC的面积为4.5.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.解:(方法一)∵点A(1,1)与B(-3,1)到y轴的距离不相等,∴直线l的斜率存在,设为k.又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.由点A(1,1)与B(-3,1)到直线l的距离相等,∴直线l的方程是y=2或x-y+2=0.得("|" k"-" 1+2"|" )/√(k^2+1)=("|-" 3k"-" 1+2"|" )/√(k^2+1),解得k=0或k=1.(方法二)当直线l过线段AB的中点时,A,B两点到直线l的距离相等.∵AB的中点是(-1,1),又直线l过点P(0,2),∴直线l的方程是x-y+2=0.当直线l∥AB时,A,B两点到直线l的距离相等.∵直线AB的斜率为0,∴直线l的斜率为0,∴直线l的方程为y=2.综上所述,满足条件的直线l的方程是x-y+2=0或y=2.

两点间的距离公式教学设计人教A版高中数学选择性必修第一册
一、情境导学在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小?二、探究新知问题1.在数轴上已知两点A、B,如何求A、B两点间的距离?提示:|AB|=|xA-xB|.问题2:在平面直角坐标系中能否利用数轴上两点间的距离求出任意两点间距离?探究.当x1≠x2,y1≠y2时,|P1P2|=?请简单说明理由.提示:可以,构造直角三角形利用勾股定理求解.答案:如图,在Rt △P1QP2中,|P1P2|2=|P1Q|2+|QP2|2,所以|P1P2|=?x2-x1?2+?y2-y1?2.即两点P1(x1,y1),P2(x2,y2)间的距离|P1P2|=?x2-x1?2+?y2-y1?2.你还能用其它方法证明这个公式吗?2.两点间距离公式的理解(1)此公式与两点的先后顺序无关,也就是说公式也可写成|P1P2|=?x2-x1?2+?y2-y1?2.(2)当直线P1P2平行于x轴时,|P1P2|=|x2-x1|.当直线P1P2平行于y轴时,|P1P2|=|y2-y1|.

两直线的交点坐标教学设计人教A版高中数学选择性必修第一册
1.直线2x+y+8=0和直线x+y-1=0的交点坐标是( )A.(-9,-10) B.(-9,10) C.(9,10) D.(9,-10)解析:解方程组{■(2x+y+8=0"," @x+y"-" 1=0"," )┤得{■(x="-" 9"," @y=10"," )┤即交点坐标是(-9,10).答案:B 2.直线2x+3y-k=0和直线x-ky+12=0的交点在x轴上,则k的值为( )A.-24 B.24 C.6 D.± 6解析:∵直线2x+3y-k=0和直线x-ky+12=0的交点在x轴上,可设交点坐标为(a,0),∴{■(2a"-" k=0"," @a+12=0"," )┤解得{■(a="-" 12"," @k="-" 24"," )┤故选A.答案:A 3.已知直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,若l1⊥l2,则点P的坐标为 . 解析:∵直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,且l1⊥l2,∴a×1+1×(a-2)=0,解得a=1,联立方程{■(x+y"-" 6=0"," @x"-" y=0"," )┤易得x=3,y=3,∴点P的坐标为(3,3).答案:(3,3) 4.求证:不论m为何值,直线(m-1)x+(2m-1)y=m-5都通过一定点. 证明:将原方程按m的降幂排列,整理得(x+2y-1)m-(x+y-5)=0,此式对于m的任意实数值都成立,根据恒等式的要求,m的一次项系数与常数项均等于零,故有{■(x+2y"-" 1=0"," @x+y"-" 5=0"," )┤解得{■(x=9"," @y="-" 4"." )┤

直线的点斜式方程教学设计人教A版高中数学选择性必修第一册
【答案】B [由直线方程知直线斜率为3,令x=0可得在y轴上的截距为y=-3.故选B.]3.已知直线l1过点P(2,1)且与直线l2:y=x+1垂直,则l1的点斜式方程为________.【答案】y-1=-(x-2) [直线l2的斜率k2=1,故l1的斜率为-1,所以l1的点斜式方程为y-1=-(x-2).]4.已知两条直线y=ax-2和y=(2-a)x+1互相平行,则a=________. 【答案】1 [由题意得a=2-a,解得a=1.]5.无论k取何值,直线y-2=k(x+1)所过的定点是 . 【答案】(-1,2)6.直线l经过点P(3,4),它的倾斜角是直线y=3x+3的倾斜角的2倍,求直线l的点斜式方程.【答案】直线y=3x+3的斜率k=3,则其倾斜角α=60°,所以直线l的倾斜角为120°.以直线l的斜率为k′=tan 120°=-3.所以直线l的点斜式方程为y-4=-3(x-3).

直线的两点式方程教学设计人教A版高中数学选择性必修第一册
解析:①过原点时,直线方程为y=-34x.②直线不过原点时,可设其方程为xa+ya=1,∴4a+-3a=1,∴a=1.∴直线方程为x+y-1=0.所以这样的直线有2条,选B.答案:B4.若点P(3,m)在过点A(2,-1),B(-3,4)的直线上,则m= . 解析:由两点式方程得,过A,B两点的直线方程为(y"-(-" 1")" )/(4"-(-" 1")" )=(x"-" 2)/("-" 3"-" 2),即x+y-1=0.又点P(3,m)在直线AB上,所以3+m-1=0,得m=-2.答案:-2 5.直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 . 解析:直线在两坐标轴上的截距分别为1/a 与 1/b,所以直线与坐标轴围成的三角形面积为1/(2"|" ab"|" ).答案:1/(2"|" ab"|" )6.已知三角形的三个顶点A(0,4),B(-2,6),C(-8,0).(1)求三角形三边所在直线的方程;(2)求AC边上的垂直平分线的方程.解析(1)直线AB的方程为y-46-4=x-0-2-0,整理得x+y-4=0;直线BC的方程为y-06-0=x+8-2+8,整理得x-y+8=0;由截距式可知,直线AC的方程为x-8+y4=1,整理得x-2y+8=0.(2)线段AC的中点为D(-4,2),直线AC的斜率为12,则AC边上的垂直平分线的斜率为-2,所以AC边的垂直平分线的方程为y-2=-2(x+4),整理得2x+y+6=0.

人教版高中政治必修4创新是民族进步的灵魂说课稿(二)
“蛟龙号”深潜器的总设计师——中船重工第七〇二研究所的徐芑南,他先后三次被评为江苏省和无锡市劳模,曾被评为上海市科技功臣,有十几个国家、部、省、市级科技进步奖项与他的名字相联。在徐芑南眼中,这些都只是“副产品”,为国家设计出最需要的潜水器,让中国具备从“浅蓝”走向“深蓝”的能力,这才是他最大的愿望。每当说到大洋的海底世界,徐芑南的语速快了起来:“海底有好多资源,等着我们去发现、去利用,我们不能落在别人的后面!”海底有石油,海底有许多未知的生物,还有锰结核、钴结壳、热液硫化物……“蛟龙号”的立项目的就是为了探明神秘的深海世界,造福人类。探究活动二:结合材料和教材,阐述创新与人类思维方式变革的关系。(设计意图)通过学生们感兴趣的材料,对本课的教学难点加以突破。

人教版高中政治必修3感悟当代中国的先进文化教案
3、探究四:课本P115《民族的科学的大众的号角》提出问题:为什么说中国特色社会主义文化是“民族的”、科学的”、“大众的”?老师引导,学生自主学习,共同合作归纳出:民族的:代表和维护中华民族的根本利益,渊源于中华民族五千多年文明,植根于中国社会主义现代化建设的实践是先进文化的立身之本。科学的:以马克思主义为指导,积极吸收了所有的科学的、进步思想的思想文化。大众的:植根于中国最广大人民群众的社会主义现代化建设的实践,体现和满足人民群众不同的层次的精神需求。4、通过视频舞蹈《较量》,创设情景(1.>只选了中国传统的哪类乐器?意图是什么?2、>与你刚才所看到的军人舞蹈有何区别,它最特殊的魅力在哪里?),点拔学生比较、分析,引入下一环节。5、温故知新:结合以上探究及视频,共同探讨:在当代中国,我们应该建设什么样的先进文化? 怎样建设中国特色社会主义文化?

人教版高中政治必修4创新是民族进步的灵魂精品教案
一、教材分析作为世界观,辩证法昭示我们,世界是一个永不停息地运动、变化和发展的世界;作为一种思维方法,辩证法要求我们以批判精神和创新意识对待周围的世界。把握唯物辩证法的革命批判精神和辩证否定观的基本内涵,有助于我们自觉树立创新意识,有助于我们坚持解放思想、实事求是、与时俱进。二、教学目标1、知识目标:熟记:创新的社会作用;理解:创新的社会作用从几个角度分析的,如何分析的。2、能力目标:学会用创新的知识分析和认识事物的能力;通过学习辨证法的革命批判精神,使学生初步形成批判性思维,初步具 有在认识世界和改造世界的活动中逐步培养和形成自己的革命批判精神的能力和创新能力。3、情感态度和价值观目标:使学生坚信创新是唯物辨证法的根本要求,创新意识的哲学基础是唯物辨证法的否定观和唯物辨证法的革命批判精神
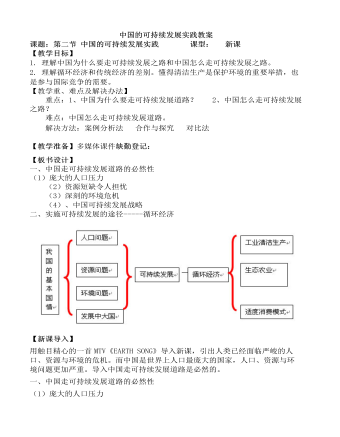
人教版高中地理必修2中国的可持续发展实践教案
1、在工业经济结构调整中,实现循环经济的基本途径是清洁生产让学生分组课前收集乡土地理中清洁生产的案例,将小组收集的案例写成小组作业。让两个小组到课堂上展示,并画出流程图。2、在农业经济结构调整中,我国大力推行生态农业,以实现循环经济留民营村的生态农业按可持续发展的观点,把保护生态环境和发展农村经济有机结合起来 主要措施:(1)调整产业结构:五业并举,全面发展 各业之间相互补充、相互促进、既保持了平衡,又促进了经济的发展 (2)开展综合利用 促进了粮食、牲畜生产的发展,增加了经济效益,降低了污染,净化了环境,有利农民健康,还改变了农田施肥结构,有效地保护了土地资源 (3)广开源流,开发利用新能源 利用太阳能和生物能,节省了以往购煤的开支,还净化了环境 意义和发展方向

人教版高中历史必修1罗马法的起源与发展说课稿
学生思考回答后归纳:随着征服地区的扩大,出现了许多新问题,新矛盾,原有的公民法已经无法适应这些新变化(质疑)。公民法适用范围限于罗马公民,用来调整他们之间的关系,罗马公民受到法律保护,并享受法律赋予的权利。在扩张中纳入到疆域中的许多外邦人不能受到法律的保护,在这种背景下,公民法发展成万民法。万民法的出现,一方面由于公民法的狭隘性,另一方面伴随对外战争的胜利,奴隶制在罗马得到快速发展。为了更加有效地保护奴隶主的私人利益,迫切需要建立和完善法律制度来维护统治阶级的利益不受侵犯。问题探究:万民法的制定产生哪些作用?学生思考回答后总结:万民法取代公民法,协调了罗马人和外邦人之间的关系及外邦人相互之间的关系,对于在庞大帝国内微细,协调各地区的民族关系、社会矛盾也祈祷重要作用。万民法使法律具有了更大的适用范围,也成为巩固罗马统治的重要工具。

人教版高中历史必修2古代商业的发展说课稿2篇
【课标要求】: 概述古代中国商业发展的概貌,了解古代中国商业发展的特点。 【教材地位】: 本课第一目“重农抑商下的古代商业”概述了各个时期商业发展的主要表现及其艰难处境;第二目“市的变迁和城市的发展”介绍了城市作为古代商业发展的中心在格局和职能等方面的变化;第三目“官府控制下的对外贸易”概述了古代中国对外贸易的概貌。 “无农不稳,无工不富,无商不活”。 古代中国商业发展的特点,决定了本课与本单元其他各部分之间具有不可分割的联系。因此,本课虽然不直接叙述农业、手工业的内容,但一定要以此前已经讲述过的农业发展及其特点、手工业发展及其特点为基础。 商业文明脱胎于农耕文明,同时又有着不一样的特质。在农耕文明的大背景下,商业在重农抑商的环境中仍顽强发展,不断突破,明清时达到鼎盛,呈现出中国商业文明特有的魅力。遗憾的是,没能像西方一样打开工业文明的大门。引导学生思考的同时,为下一节古代的经济政策做好铺垫。

人教版高中历史必修2中国民族资本主义的曲折发展说课稿2篇
2.民族工业的遭受打击自主探究4:阅读【历史纵横】和教材插图,探究抗战时期民族走向萎缩的原因有哪些?在沦陷区日军的摧毁和吞并;在国统区国民政府强化对经济的全面统治;官僚资本垄断经济命脉,压制民族工业牟取暴利。造成了什么后果?(官僚资本的膨胀,民族资本的萎缩)3、民族工业的萎缩讨论:为什么抗战胜利了,民族资本主义工业反而日益萎缩呢?学生通过合作学习,对教材提供的资料进行认真分析,认识到美国的经济掠夺、官僚资本的挤压、通货膨胀三个因素的共同作用,使民族工业陷入绝境,纷纷倒闭。抗战胜利后,国民政府虽采取了一些措施推动国民经济的发展,但是,国民政府为了取得美国的援助,不惜出卖国家主权,与美国在1946年签订《中美友好通商航海条约》,让美国在华攫取政治、经济等特权。中国民族工业纷纷破产。

人教版高中历史必修3三民主义的形成和发展说课稿2篇
在学生正确掌握了三民主义的进步性和局限性之后,提出第五个问题:三民主义的局限性是由什么决定的?这一问题学生较易回答,为进入下一目教学打下基础。二、三民主义的实践这目内容在新课导入时已经涉及,故进行略讲,主要采用谈话法,与学生一起回忆、交流。在此基础上,提出探究问题五:在三民主义指导下,孙中山先生进行的一系列革命斗争其结局怎样?为什么会这样?第一问学生较易回答,第二问我组织学生进行交流、讨论。在学生回答的基础上,我将向学生指出:由于三民主义的局限性,它不能指导中国民主革命走向成功,中国革命呼唤新的理论指导。从而过渡到下一目教学。三、旧三民主义发展为新三民主义1、背景:情境再现,激发兴趣分析资料,感悟新知多媒体播放电影《孙中山》片段让学生感受在一系列革命斗争失败后,孙中山先生的彷徨、思索。

人教版高中历史必修3现代中国教育的发展说课稿
一、教材分析下面我来谈一谈对教材的认识:主要从教材的地位和作用、以及在此基础上确立的教学目标、教学重难点这三个方面来谈。首先,来谈教材的地位和作用:本课教材内容主要从三个方面向学生介绍了现代中国教育的发展状况和趋势:人民教育的奠基、动乱中的教育和教育的复兴,全面讲述了新中国教育的三个阶段。本课是文化史中中国史部分的最后一课, 也是必修三册书中唯一涉及教育的一课。而教育是思想文化史中的重要组成部分,江泽民同志在谈到教育的时候曾经说过,“百年大计,教育为本。教育为本,在于育人”。教育是关系国计民生的大事。学生通过学习新中国教育发展的史实,理解“科教兴国”、“国运兴衰,系于教育”的深刻含义。最终由此激发学生树立“知识改变命运、读书成就人生”的信念,树立勤奋学习、成人成才、报效祖国、服务社会的崇高理想。故本课的教学有极大的现实意义。谈完了教材的地位和作用,我再分析一下教学目标:

人教版高中地理必修2第六章第二节中国的可持续发展实践说课稿
1.导入新课:用触目精心的一首MTV《EARTHSONG》导入新课,引出人类已经面临严峻的人口、资源与环境的危机。而中国是世界上人口最庞大的国家,人口、资源与环境问题更加严重。既然我们知道了可持续发展的概况,了解了它的发展过程,从上节课内容的分析中,也理解了作为人类的发展,可持续是唯一的选择,也是我们所追求的目标,那么,具体到我们国家、我们周围的生产、生活情况又该如何呢?2.新课讲授:首先,通过三则补充材料的案例和课本上的内容分别说明庞大的人口压力,资源短缺和不合理利用,深刻的环境危机方面的问题,得出走可持续发展之路是我国的必然的唯一的选择。接着通过《中国21世纪议程》——中国21世纪人口环境与发展的白皮书的过渡引出实施可持续发展的途径。在这部分内容的讲解上,主要通过其中一种主要途径-循环经济的讲解,特别是对清洁生产和生态农业的具体分析,总结出中国走可持续发展之路事在必行,行必有果。再通过完成课本上最后一个活动题对本节内容进行深化。

人教版高中地理必修2中国的可持续发展实践精品教案
师:对。具体说一说沼气池在这个系统中为什么居于核心纽带地位。生:因为沼气池充分利用了生产过程的废料,实现了清洁生产,减少了浪费和污染,而且很好地实现了生态循环。师:不错!留民营生态农业的实质就是:地尽其利,物尽其用,最大限度地循环利用资源和消除环境污染,达到节约、高效的目的,真正实现了生态效益、经济效益、社会效益三方面的高度统一,实现了可持续发展。师:实施可持续发展战略必须依靠公众的支持和参与,我们每一个人都应该从自身做起,那我们可以在日常生活中可以采取哪些有益于可持续发展的行动? 生1:节约粮食、爱惜粮食。生2:不乱扔垃圾,垃圾分类回收。生3:不开“无人灯”。生4:节约用电、用水。生5:减少空调的使用,在冬夏季分别降低、提高空调温度的设置。

国际博物馆日国旗下讲话稿:平台之上的人生
早上好!今天是5月18日,国际博物馆日。有人说,了解一个地方的过去和现在是从博物馆开始的,还有人说博物馆如同历史长河,源源不断的将过去的故事输送到你的面前,是啊,每当你站在博物馆里,就仿若乘一叶扁舟,溯时间之河,穿过空间的阻隔,尽览历史的变迁,这是多么优美的意境啊!同学们,你们对博物馆有多少了解?你们知道博物馆有着怎样的历史吗?你知道世界五大博物馆分别指哪里吗?今天,让我们来一次奇妙的博物馆之旅,与历史、与文明进行一次深度对话。约在公元前五世纪,在希腊的特尔费·奥林帕斯神殿里,有一座收藏各种雕塑和战利品的宝库,他被博物馆界视为博物馆的开端。1753年,大英博物馆建立,成为全世界第一个对公众开放的现代意义的大型博物馆。1974年6月,国际博物馆协会与哥本哈根召开第十一届会议,将博物馆定义为“一个不追求赢利为社会和社会发展服务的公开的永久机构”。1977年国际博物馆协会为促进全球博物馆事业的健康发展,吸引全社会公众对博物馆事业的了解、参与和关注,向全世界宣告:1977年5月18日为第一个国际博物馆日,并每年为国际博物馆日确定活动主题,XX年的主题是:博物馆致力于社会的可持续发展。而法国的卢浮宫,英国的大不列颠博物馆,美国的大都会博物馆,俄罗斯的艾米塔什博物馆,中国的故宫博物馆位列世界五大博物馆行列。

人教版高中地理选修2山区农业资源开发的地理背景教案
图7.1“我国南方低山丘陵区的大致范围”南方低山丘陵区的大致范围大致是指淮河以南、云贵高原以东、雷州半岛以北,对照同纬度世界其它地区的地表景观,得出本区是回归沙漠带上的“绿洲”。根据本区的纬度位置和海陆位置掌握本区的气候类型、气候特点以及这种气候影响下的生物资源、土地资源、水资源的特点。【教学内容】一、回归沙漠带上的“绿洲”1、 位置范围:南方低山丘陵区地域广阔,其范围大致是指淮河以南、云贵高原以东、雷州半岛以北广大的低山丘陵地区。2、 区位优势:与世界上同纬度其他地区相比,南方低山丘陵区处于亚热带、湿润区,具有温暖湿润的环境,成为回归沙漠地带的“绿洲”,与全国其他地区相比,南方低山丘陵区开发潜力巨大。

人教版高中地理选修2浦东新区的规划和开发教案
1、图12.5“浦东新区的规划图”首先了解浦东新区的位置,浦东新区位于黄浦江东部,东临东海,北濒长江,面积广阔,地形平坦,和上海市繁华的外滩和南京路只有一江之隔;其次要了解城市规划的功能分区。2、图12.6“浦东新区图”图中可见已建成陆家嘴、张江、金桥、外高桥、孙桥等功能分区,理解浦东作为现代化城市新区的格局已基本形成。3、图12.8“浦东新区的产业结构图(1997年)”读此图应该明确,浦东新区国民经济的主要支柱是工业,第二产业占62.1%,比重最小的是第一产业,仅占0.8%,为充分发挥浦东新区的龙头作用,今后该区应继续把第二产业放在首要位置,成为上海市高新技术产业和现代工业的基地。【教学内容】一、浦东新区的开发条件和作用建设城市新区是上海市发展的必然选择,建设新城区首先要选择合适的区域。

高教版中职数学基础模块下册:9.1《平面的基本性质》教学设计
课题序号 授课班级 授课课时2授课形式新课授课章节 名称§9-1 平面基本性质使用教具多媒体课件教学目的1.了解平面的定义、表示法及特点,会用符号表示点、线、面之间的关系—基础模块 2.了解平面的基本性质和推论,会应用定理和推论解释生活中的一些现象—基础模块 3.会用斜二测画法画立体图形的直观图—基础模块 4.培养学生的空间想象能力教学重点用适当的符号表示点、线、面之间的关系;会用斜二测画法画立体图形的直观图教学难点从平面几何向立体几何的过渡,培养学生的空间想象能力.更新补充 删节内容 课外作业 教学后记能动手画,动脑想,但立体几何的语言及想象能力差